复杂环境下多目标多无人机协同任务规划

张 哲，吴 剑,2，何 诚，穆忠伟

(1.南昌航空大学，南昌 330063；2.洪都航空工业集团650所，南昌 330024)

在复杂战场环境中，多无人机协同任务规划已成为提高无人机作战自主性和作战效能的关键技术[1]。尤其是在复杂战争环境下，面对威胁源和大量搜索目标群时，如何快速准确地协同任务规划是当前的一大难题[2-5]。

针对多目标多无人机协同任务规划问题，目前主要研究的模型有多车辆路径(MVRP)[6-7]、多维多选择背包[8]、多旅行商(MTSP)[9-10],混合整数线性规划(MILP)[11-12]和动态网络流优化(DNFO)[13]等。MVRP模型更多地描述任务分配中有关时间的约束，而未充分考虑无人机的动力学特性。MMKP和MTSP模型并未讨论任务的异构性。MILP和DNFO模型仅适用于范围小、目标数量少和环境威胁源单一的任务规划问题。Mahesh等[14]提出的将多机协同问题抽象为多个相互独立的TSP问题，优化指标为最短路线长度，然后利用模拟退火算法去进行解决，该方法虽然降低了问题的复杂程度，但是忽略了协同的本质。

本文在上述研究的基础上，针对复杂环境中雷达站和无人机载荷约束之间的任务均衡性，在充分了解地形情况和敌方目标信息的情况下，建立了多目标多无人机协同任务规划模型。将多目标规划问题转化为单目标规划，并且运用主客观赋权法计算各指标的权重。探讨了利用改进遗传算法去求解模型，加快了收敛速度，提高了任务规划效率。最后根据任务载荷的约束，对规划路线进行了优化，给出了多机协同的任务规划方案。

1 多无人机协同任务规划模型

某作战部队配有7个无人机基地，分别记为P01～P07，各基地均配备若干数量的FY系列无人机。为了完成目标侦查、通信中继、作战攻击等任务，其中指派FY-1型无人机主要完成目标侦查及作战攻击，根据任务要求，无人机需完成侦查和打击的目标群为A01～A10，每个目标群包含多个地面目标，周围均配有雷达站。无人机基地的相关信息如表1所示。

表1 无人机基地的相关信息

1.1 多机协同任务规划的目标函数

多无人机多目标协同任务规划主要从时域协同和空域协同两个方面进行建模分析，给出这两方面的4个规划目标函数。对于时域协同：以完成任务所需的时间代价为子目标函数，无人机从不同的基地出发，分别以不同时间点到达任务目标的指定位置，体现了无人机在任务规划时间上的无缝衔接。对于空域协同：以无人机可飞行空域内滞留雷达区的路程、完成攻击目标任务时的收益以及执行侦查任务时造成的威胁代价为各子目标函数，保障无人机能够安全到达目标区域，避免防空威胁以及碰撞。

1)飞行总路程

设一个赋权无向完全图G=(C,X,D),目标群集合C={c1,c2,…,cn},边集合x={xij|i,j=0,1,2,…,n},Xij为目标群Ci到目标群Cj的边,表示该条飞行线路是否应该执行。距离集合D={dij|i=1,2,…,n}表示目标群Ci到目标群Cj的距离。

给定m架无人机，无人机从任一基地bi出发。首先飞向目标群Ci，沿一条路径侦查并且从目标群Cj(Ci≠Cj)离开。每架无人机都至少到达一个目标群，任意目标群都需要被无人机侦查且仅被侦查一次。求m条路径，使得m架无人机的飞行总路程L1最小。在讨论雷达对无人机协同飞行的影响时，可以将问题抽象为二维平面的路线规划问题，使得无人机在敌方雷达探测范围内的飞行路径最短。由于多架无人机从不同的基地起飞，且每架无人机到达第一个目标群和离开最后一个目标群都会增加滞留在雷达探测区内的路程2R(R为雷达探测半径)。

令Si={cin,ck,…，cout}为第i架无人机飞行路线，其中cin和cout为第i架无人机侦查路线的起点和终点。求总路线S={s1,s2,…,sm}，使得:

(1)

2)攻击目标收益

攻击目标收益[15]是指多无人机在协同完成任务时对目标造成的毁伤价值。它可定义为目标价值和毁伤概率的函数，该函数指向了无人机协同任务攻击时的作战效能最大化。记第i架无人机攻击目标群Cj所带来的效益为P，有：

(2)

(3)

3)完成任务所需时间

完成任务所需时间定义为:

t= maxti

(4)

式(4)中，ti为第i架无人机完成规划任务所花费的时间。考虑各无人机间任务分配和载荷资源的合理性，给出时间代价函数L3，即：

(5)

4)执行任务时造成的威胁

当无人机协同飞行时，假设第i架无人机经过目标群Cj后的生存概率为PBi,则PBi=1-PKj。对任一无人机来说，执行n个任务时造成的威胁代价L4：

(6)

1.2 任务规划模型

多无人机协同任务规划是多基地的无人机针对多目标群进行侦查和打击等任务，实质上是多目标优化与决策问题[16]。通过建模分析，运用线性加权和法将多目标规划转化为单目标规划问题。由于在转化过程中各目标函数有不同的量纲，采用线性变换法进行归一化处理，将各目标函数的量纲转变为[0,1]内的具体数值。因此可以得到多无人机协同的任务规划模型为：

(7)

约束条件：

(8)

式(7)、式(8)中：ω={ω1,ω2,ω3,ω4}为各目标函数所占的权重；d()表示无人机从目标群飞回基地的距离；M为无人机最大航程；s为燃料安全系数；xij∈{0,1}为决策变量，xij=1表示第i架无人机对第j个目标群执行任务；N表示目标群数量；Oi为第i架无人机的任务载荷。

约束条件使得无人机至少侦查一个目标，并且所有目标有且仅有一次被无人机侦查。因此，各无人机之间轨迹无重合。考虑到无人机在各点之间飞行需要转向，为增大安全性，经过初步计算一架无人机不能飞完全程，设定转弯次数为目标数量的一般，即34次，每次转弯角度为180°，目标群数量N为10，安全系数s为1.05。

2 基于改进遗传算法的模型求解

2.1 算法改进方案

多无人机协同任务规划模型的求解实质上可以看成是对多旅行商(MTSP)问题的求解。由于旅行商问题属于NP问题，因此通常采用启发式优化算法对模型进行求解。

由于传统的遗传算法在求解MTSP问题时，容易陷入局部最优解。为了提高算法的执行效率，较快得到全局最优解，对算法进行以下改进：1)只保留最优父代，加速收敛;2)采用多岛遗传形式[17]，保持解的多样性;3)使用无性繁殖策略[18]，提升了收敛速度，并通过多种交叉和变异方式，避免提前收敛于局部最优解。

2.2 算法实现

2.2.1编码

每一个体的染色体长度为n+m-1,其中染色体前n位为随机的整数,呈乱序排列，按大小排序后即为无人机侦查各目标点的顺序。后m-1位为断点位置的标号，断点用来表示目标在不同无人机之间的分配。一条染色体G={4,7,1,9,3,6,3,…|2,5}。其中该染色体对应的目标数为n，其对应的无人机数量为m=3，后半部分的断点2和5表示三架无人机分别侦查攻击以下标号的目标为：4→7; 1→9→3; 6→3→…→n。

2.2.2种群

将种群分为多个组，每个组的个体数量为8，组的数量根据模型需要设置为10个。每组内的个体之间相互交叉无障碍，交叉和变异概率pc为0.875，pi为0.01，即组中个体有很小的几率逃逸到另一个组中。初始种群生成。

2.2.3适应度计算及选择策略

适应度函数为各目标函数，取每个岛屿中适应度函数最高(目标函数最小)的个体为父代。为了加速收敛，直接删除该岛屿中其他的个体。

2.2.4遗传运算

采用多种遗传方式来生成子代，具体规则如下：

步骤(1)对换染色体前半段的任意两个数;

步骤(2)对换染色体前半段的两个数段，即同时将多个数进行对换;

步骤(3)对染色体前半段的数进行左移操作;

步骤(4)随机更新染色体后半段;

步骤(5)同时进行步骤(1)和步骤(4);

步骤(6)同时进行步骤(2)和步骤(4);

步骤(7)同时进行步骤(3)和步骤(4);

步骤(8)染色体不变。

2.2.5终止规则

将最大迭代次数作为终止条件，设置最大迭代次数为200。

2.2.6算法流程图

算法流程如图1所示。

图1 算法流程框图

2.3 计算各指标的权重

通常计算权重的方法可以分为主观赋权法和客观赋权法。前者如层次分析法、专家调查法等，该方法反映了决策者的意向，导致了评价和结果具有很大的主观随意性。后者如主成分分析法、熵值法等，该方法虽然具有客观的理论依据，但没有考虑决策者的意向。故采取主客观综合赋权法[19](基于熵权的组合赋权法)确定各目标函数的权重。

通过将不同指标上的专家主观信息与客观信息进行融合，计算相邻指标间的客观熵权值之比，进而得到各指标的权重。具体步骤如下：

步骤1由专家确定指标的重要性排序。在指标体系准则层中共有L个准则，而在第i个准则层共有Mi项指标。专家需要对K个待评估对象给出不同准则下所有∑Mi个指标的重要性排序(i=1,2,…,L)。

步骤2计算各指标所对应的熵权值。设第k个待评估对象在第i个准则第j项指标下的数据为vij，特征比重为hijk，则

(9)

式(9)中：i=1,2,…,L;j=1,2,…,Mi;k=1,2,…,K。设eij为第i个准则层第j项指标的熵值，则：

(10)

第i个准则层第j项指标的熵权值为μij，则：

(11)

步骤3计算相邻指标的重要程度。设ri, j-1为第i个准则中第j-1项指标的重要程度,则有：

(12)

式(12)中：i=1,2,…,L;j=2,…,Mi。

步骤4计算指标对准则的权重。设fi,Mi为第i个准则下第Mi项指标对准则i的权重，则：

(13)

第i个准则下其他Mi-1项指标的权重可通过其后一项指标的权重计算得到，即：

fi, j-1=ri, j-1·fi, j

(14)

步骤5计算指标权重。设μi为第i个准则的熵权，ri-1为相邻的第i-1个准则相对于第i个准则的重要程度，则有：

(15)

(16)

设ωL为第L个准则的权重，则：

(17)

其他L-1个准则的权重为：

ωi-1=ri-1·ω

(18)

因此，第i个准则第j项指标的权重为：

ωij=fij·ωi

(19)

式(19)中：i=1,2,…,L;j=1,2,…,Mi。

多无人机协同任务规划能力的评价指标体系如图2所示。

图2 任务规划能力的评价指标体系框图

3 仿真分析

为了验证多无人机多目标任务协同规划模型及改进遗传算法，在PC机配置为Intel(R)Core i5-4210M @2.60 GHz,MatlabR2017a环境下完成模型和算法的仿真实验。无人机上加载的S-1、S-2两种载荷用于对目标群实现侦查和攻击任务。设定无人机飞行速度为200 km/h，高度为1 500 m，最大飞行时间为10 h，无人机每次只能加载一种载荷。目标群数量N=10，目标点个数n=68,各目标函数的权重ω={0.352,0.287,0.145,0.216}，根据改进遗传算法流程，设置最大迭代次数为200。计算得到了所有目标点间的任务规划如图3所示。

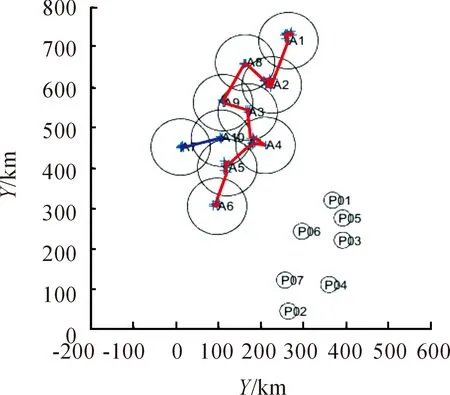
图3 目标点间任务规划结果

由于无人机上加载S-1和S-2两种载荷，根据目标点间任务规划的结果，分别对无人机加载两种载荷后的航迹进行优化。给出了加载两种载荷的无人机任务规划示意图如图4和图5。

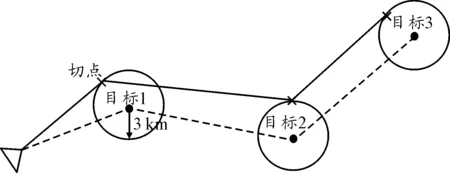
图4 加载S-1型载荷航迹示意图

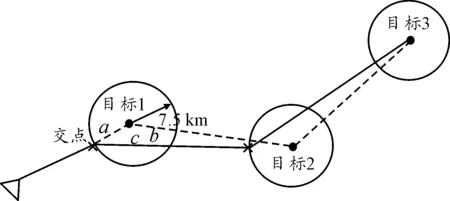
图5 加载S-2型载荷航迹示意图

图4、图5中虚线为目标点间规划的结果，实线为根据两种不同载荷限制而规划的无人机航迹。对于加载S-1型载荷：无人机从基地起飞向目标1飞行过程中，直接到达目标1所在圆的切点，直至侦查任务完成后飞回基地。对于加载S-2型载荷：无人机从基地直接到达与目标1所在圆的交点，完成对目标1的攻击后，飞往目标2，直接到达目标2所在圆的交点，直至最终飞回基地。线段a和线段b分别为无人机根据最短线飞向目标1和目标2的路径。线段c是无人机完成对目标1攻击任务后飞向目标2的路径。

加载S-1型载荷的无人机协同任务规划仿真结果如图6所示，A4目标群局部任务规划仿真结果放大图如图7。

图6 加载S-1型载荷的协同任务规划仿真结果

加载S-2型载荷的无人机协同任务规划仿真结果如图8所示，A4目标群局部任务规划放大图如图9，改进遗传算法与传统遗传算法如图10所示，协同任务规划调度方案内容见表2。

由于载荷S-1为光学成像传感器，采用广域搜索模式对目标进行成像，达到一定的目标识别精度。载荷S-2是目标指示器，为制导炸弹提供目标指示，用于攻击作战任务。S-1载荷带宽为2 km，S-2载荷要求距被攻击目标的距离小于7.5 km，对每个目标安排S-1、S-2两种载荷各自至少使用一次，而且两种载荷对同一目标的侦查间隔不超过4 h。因此，仿真结果中两种载荷对任务规划路线优化的航迹点不同，实现了无人机目标侦查和作战任务的协同规划。

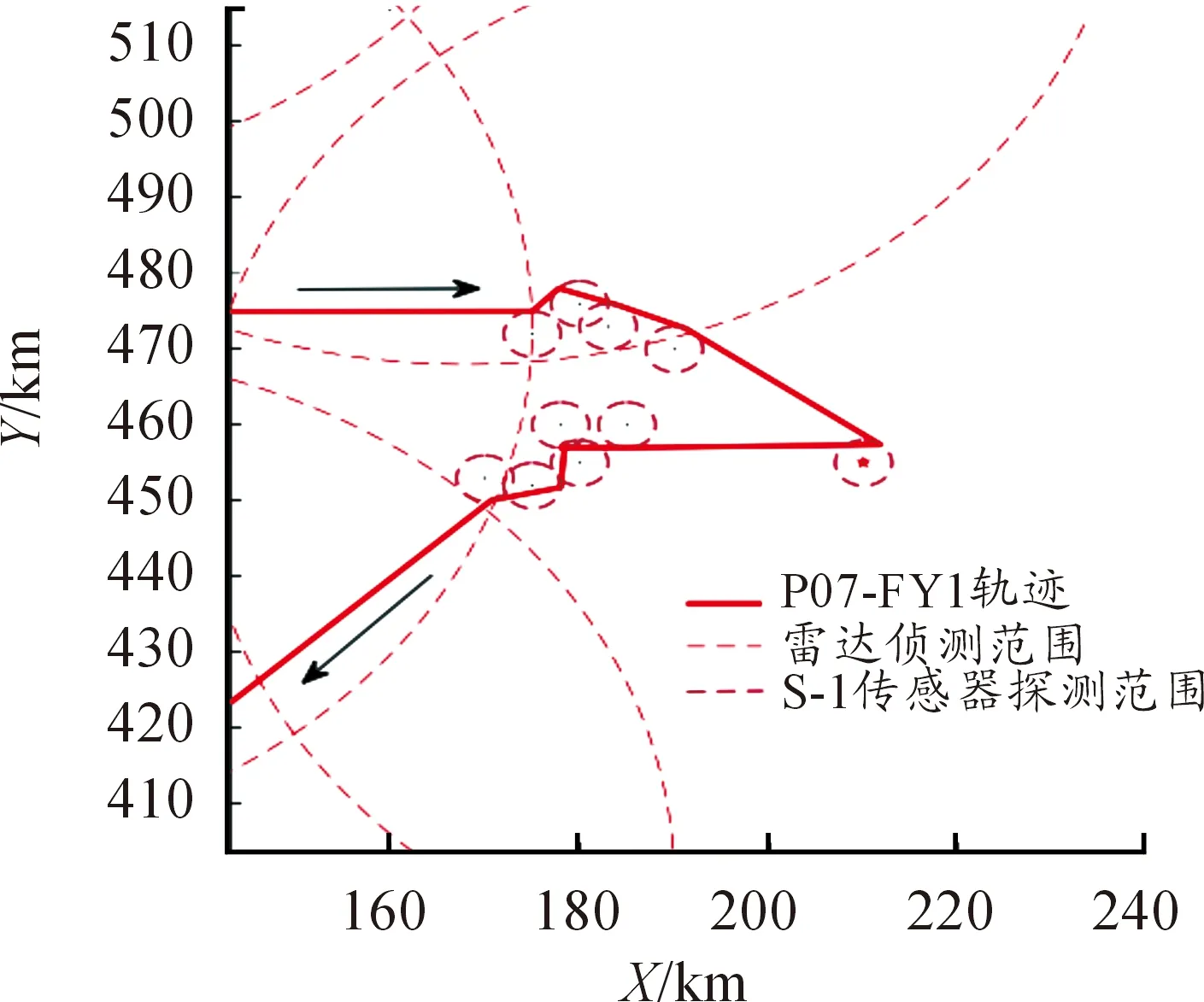
图7 S1-A4目标群局部任务规划放大图

图8 加载S-2型载荷的协同任务规划仿真结果

图9 S2-A4目标群局部任务规划放大图

图10 两种算法的比较

表2 多机协同任务规划调度方案内容

4 结论

在分析影响任务规划关键指标的基础上，以考虑雷达站影响下无人机飞行总航程、攻击目标收益、执行任务的威胁代价以及任务完成时间等指标为目标函数，建立了多机协同任务规划模型。运用主客观综合赋权法确定了各指标所占比重，使得模型更加准确。结合改进的遗传算法对模型进行求解，加快了收敛速度，任务规划效率显著提高。最后考虑到无人机的转弯以及载荷约束，对任务规划路线进行了优化。仿真结果验证了本文方法的有效性。