土壤液塑限联合测定仪测量结果的不确定度评定与分析

王锦清

1.福建省交通科研院有限公司，中国·福建 福州 350004

2.福建省交科计量技术有限公司，中国·福建 福州 350004

土壤液塑限检测仪；测量结果；不确定；应用

1 引言

测量不确定度是与测量结果相联系的参数，表征合理地赋予被测量值的分散性；是对其真值所处范围的评定，是对分量结果质量的定量评价。

根据ISO/IEC 17025:2017《检测和校准实验室能力的通用要求》和JJF1069-2016《法定计量检定机构考核规范》的要求，当对测量设备进行校准并出具校准证书时，应给出测量结果和测量不确定度；对建立计量标准装置、研制测量标准及制定计量检定规程提出检定方法时，也应评定标准装置的不确定度[1]。

在交通工程行业中，测量不确定度主要在各交通领域的检测试验室、研究机构及计量检定机构的检定、校准及检测试验等工作中广泛应用。开展试验检测工作中，通过检测结果的不确定度评定，可表征试验检测结果的可靠性与合理性；而在计量检定/校准工作中，通过测量结果的不确定度评定，可表明检定/校准结果的量值溯源性是否达到要求。因此，测量不确定度是计量检定、校准及检测试验工作中不可缺少的一个重要环节[2]。

然而，在从事上述相关工作的广大技术人员中，还有很大部分对测量不确定度的评定及其标准不确定度分量的分析与计算方法不甚理解或知之甚少，这会导致测量结果的质量工作得不到保障。因此，为了广大试验检测人员和计量工作者能够更好地理解和掌握测量不确定度评定的步骤及确定标准不确定度分量方法，下面笔者以土壤液塑限检测仪测量结果的不确定度评定为例分析一下测量不确定度评定的步骤和方法，以探讨在不确定度过程中如何准确、完整地分析确定标准不确定度的分量。

2 土壤液塑限检测仪测量结果的不确定度评定

从JJG（交通）069-2006《土壤液塑限检测仪检定规程》对仪器设备的计量特性可知，其校准结果的不确定度主要来源于质量（圆锥体的质量）、长度（盛土杯尺寸、测量误差）、角度（锥尖角度）、时间（测量时间）四个方面的测量结果的不确定度。下面笔者以中国北京中科东晨科技有限公司生产的数显式土壤液塑限测定仪（型号：LP-100D；出厂编号：1910502）为例，进行分析[3]。

2.1 质量

2.1.1 数学模型

根据测量原理：用电子天平直接测量被校液塑限检测仪圆锥体的质量。

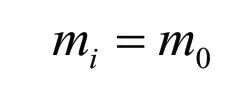
2.1.2 方差与灵敏系数

2.1.3 标准不确定度分量的分析与计算：

用电子天平对被校液塑限检测仪圆锥体的质量进行10次重复测量，测量结果如表1所示：

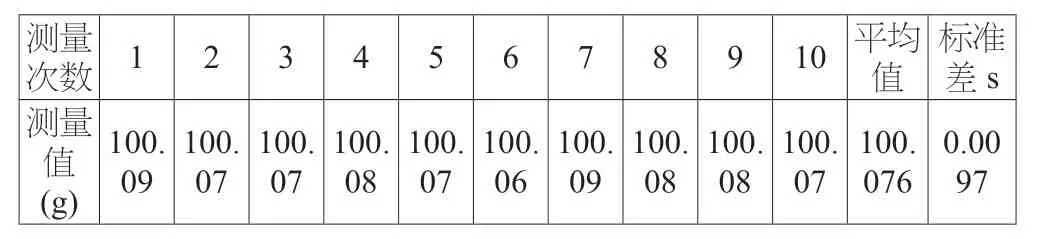
表1 测量结果

在实际测量时，重复测量三次，则测量重复性引入的标准不确定度分量为:

电子天平由上一级标准检定(e=0.1g)，准确度为II级，根据规程，测量范围为(0～2000)g 时，其最大允许误差为MPE：±1.0e(即±0.1g)，作均匀分布，取包含因子则其引入的标准不确定度分量为：

电子天平的示值分辨力d为0.01g，其半宽度为0.005g，作均匀分布，取包含因子则其引入的标准不确定度分量为：

（4）标准不确定度分量一览表

标准不确定度分量 不确定度来源 标准不确定度值 ()i ux()0 1 mu 测量重复性 0.0056g()0 2 m u本身准确度 0.0577g

2.1.4 合成标准不确定度

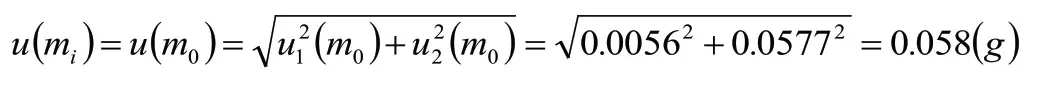
2.1.5 扩展不确定度

取包含因子 2=k，则

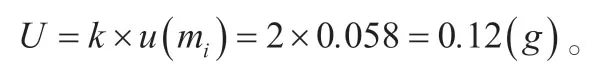
2.2 长度（以数显卡尺为标准器）

2.2.1 数学模型

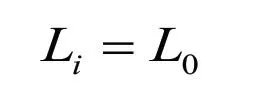
式中：Li— 被校液塑限检测仪被测量长度值(mm)；

L0— 数显卡尺的测量值(mm)。

2.2.2 方差与灵敏系数

2.2.3 标准不确定度分量的分析与计算：

用数显卡尺对被校液塑限检测仪盛土杯内径进行10次重复测量，测量结果如表2所示：

表2 测量结果

在实际测量时，重复测量三次，则测量重复性引入的标准不确定度分量为：

数显卡尺由上一级标准校准，其扩展不确定度为：U=0.03mm(k=2)，则其引入的标准不确定度分量为：

数显卡尺的示值分辨力d为0.01mm，其半宽度为0.005mm，作均匀分布，取包含因子则其引入的标准不确定度分量为：

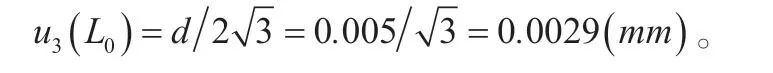
2.2.4 标准不确定度分量一览表

标准不确定度分量 不确定度来源 标准不确定度值 ()ix u()0 1 Lu 测量重复性 0.0056mm()0 2 L u本身误差 0.015mm

2.2.5 合成标准不确定度

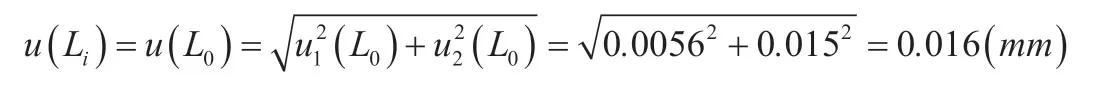
2.2.6 扩展不确定度

取包含因子 2=k，则

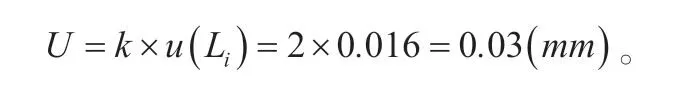
2.3 长度（以量块为标准器）

2.3.1 数学模型

式中：Δ —— 被校液塑限检测仪的测量误差(mm)

Li—— 被校液塑限检测仪的测量值(mm)

L0—— 量块的标准值(mm)

2.3.2 方差与灵敏系数

式中：u(Li) —— 被校液塑限检测仪引入的标准不确定度分量

u(L0) —— 量块引入的标准不确定度分量

c1、c2—— 灵敏系数(其中：

2.3.3 标准不确定度分量的分析与计算：

2.3.3.1 被校液塑限检测仪引入的标准不确定度分量u(Li)

（1）被校液塑限检测仪的测量重复性引入的标准不确定度分量

以10mm的标准量块对被校液塑限检测仪进行10次重复测量，测量结果如表3所示：

表3 测量结果

在实际测量时，重复测量三次，则测量重复性引入的标准不确定度分量为:

被校液塑限检测仪的示值分辨力d为0.1mm，其半宽度为0.05mm，作均匀分布，取包含因子则其引入的标准不确定度分量为：

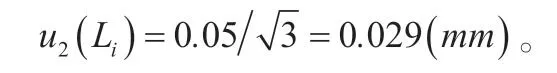
则被校液塑限检测仪引入的标准不确定度分量为：

2.3.3.2 量块引入的标准不确定度分量u(L0)

量块由上一级标准检定，准确度等级为4 等，在标称长度为10mm 时，其扩展不确定度为：U=0.22μm(k=3)，则其引入的标准不确定度分量为：

2.3.3.3 标准不确定度分量一览表

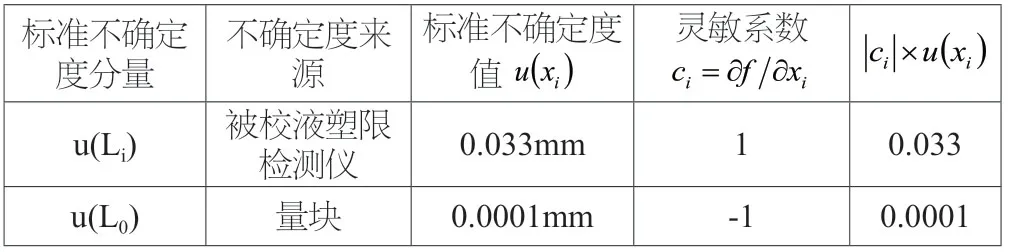
标准不确定度分量不确定度来源标准不确定度值 ()ix u灵敏系数i i xfc ∂∂=()i i xuc ×u(Li) 被校液塑限检测仪 0.033mm 1 0.033 u(L0) 量块 0.0001mm -1 0.0001

2.3.4 合成标准不确定度

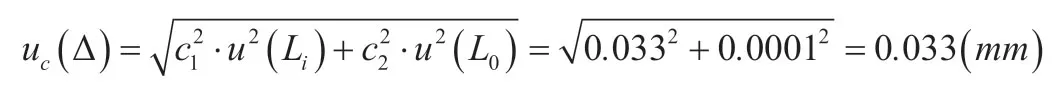
2.3.5 扩展不确定度

取包含因子 2=k，则

2.4 角度

2.4.1 数学模型

测量原理：用数显万能角度尺直接测量圆锥体锥尖的角度。

式中：θi— 被校圆锥体锥尖的角度(°)；θ0 — 数显万能角度尺的测量值(°)。

2.4.2 方差与灵敏系数：

式中：u(θi) — 被校圆锥体锥尖角度的标准不确定度

u(θ0) — 数显万能角度尺引入的标准不确定度

2.4.3 标准不确定度分量的分析与计算

用数显万能角度尺对测量圆锥体锥尖的角度进行10次重复测量，测量结果如表4所示：

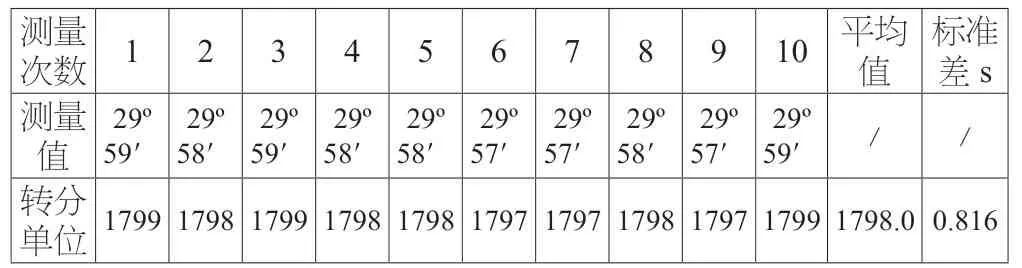
表4 测量结果

在实际测量时，重复测量三次，则测量重复性引入的标准不确定度分量为:

数显万能角度尺由上一级标准检定，其扩展不确定度为：U=1′ (k=2)，则其引入的标准不确定度分量为：

（3）数显万能角度尺的分度值d 引入的标准不确定度分量u3(θ0)

数显万能角度尺的分度值d为1′，半宽度为0.5′，作均匀分布，取包含因子则引入的标准不确定度分量为：u

（4）标准不确定度分量一览表

标准不确定度分量 不确定度来源 标准不确定度值 ()i ux u1(θ0) 测量重复性 0.471′u2(θ0) 本身准确度 0.5′

2.4.4 合成标准不确定度

2.4.5 扩展不确定度

2.5 时间

2.5.1 数学模型

测量原理：用电子秒表直接被校液塑限检测仪的测量时间。

式中：it— 被校液塑限检测仪的测量时间(s)；0t— 电子秒表的测量值(s)。

2.5.2 方差与灵敏系数

2.5.3 标准不确定度分量的分析与计算

用电子秒表对被校液塑限检测仪的测量时间进行10次重复测量，测量结果如表5所示：

表5 测量结果

在实际测量时，重复测量三次，则测量重复性引入的标准不确定度分量为：

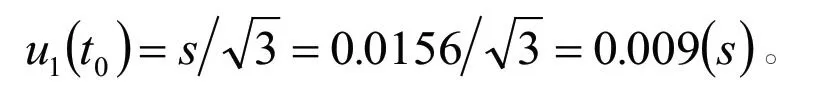
电子秒表由上一级标准检定，其最大允许误差为MPE：±0.10s，作均匀分布，取包含因子则其引入的标准不确定度分量为：

电子秒表的示值分辨力d为0.01s，其半宽度为0.005s，作均匀分布，取包含因子则其引入的标准不确定度分量为：

2.5.4 标准不确定度分量一览表

2.5.5 合成标准不确定度

2.5.6 扩展不确定度

取包含因子 2=k，则

3 测量不确定度的分析与探讨

3.1 测量不确定度评定的流程

从上述测量不确定度评定的过程来看,评定测量不确定度的一般流程具体如下:①分析不确定度来源和建立数学模型→②通过对数学模型进行分析,确定标准不确定度公式,进而得出各标准不确定度分量→③评定标准不确定度分量ui→④计算合成标准不确定度ui→⑤确定扩展不确定度U →⑥报告测量结果的不确定度。

3.2 标准不确定度分量的确定

由上述例子可以看出,评定标准不确定度分量ui在整个评定过程中是最主要的。那么,如何来完整、准确地分析和确定各标准不确定度分量呢?归纳起来主要有以下几点:

①通过对数学模型分析确定的标准不确定度公式，可以得出各主要标准不确定度分量。

②分析各主要标准不确定度分量中可能存在的所有不确定度分量。

③在分析标准不确定度分量时，无论简单还是复杂，均可从设备、环境、方法和人员四个方面的因素来分析，并要充分考虑在实际测量过程中有哪些因素会影响结果的不确定度分量，做到不遗漏、不重复[4]。

4 结语

论文通过阐述测量不确定度的定义及其在交通行业中的应用，论述了土壤液塑限测定仪测量结果的不确定度评定，分析了测量不确定度评定流程，并提出了相应的解决方法，进而保证了测量不确定度结果的准确、可靠，并可为相关计量、试验技术人员进行不确定度评定工作提供一定的参考。