含有时滞和非局部条件的分数阶阻尼系统解的存在唯一性
2020-03-21盛家乐盛家喜
盛家乐,盛家喜①
(1.安徽大学 数学科学学院,安徽 合肥230601;2.合肥师范学院 数学与统计学院,安徽 合肥230601)
0 引言
分数微积分作为传统整数阶微积分的推广,其概念早在1695 年已由LEIBNUZ 和L′HOSPITAL 提出. 然而,直到20世纪60年代末,工程师们才开始对分数阶微积分感兴趣,因为分数阶微积分对某些系统的描述更为准确. 从那时起,分数微积分越来越多地被用于科学和工程的各个领域中对真实系统的行为进行建模. 近年来,分数阶微分方程在工程、物理、经济等诸多领域的建模中得到广泛的应用. 更详细的关于分数阶微积分的知识可参考文献[1-4].
分数阶振动方程[5-7]是经典谐振子方程的推广,用分数阶导数代替二阶导数,即

在此基础上,许多作者开始研究一类线性多项分数阶系统,如具有弹簧、质量和粘弹性阻尼的机械系统

x(t)表示质量与其他分量组合的位置,f(t)表示一个力函数,m,k1和k2表示力学常数. 此外,该模型还考虑描述某些气体在流体中溶解的动力学和球浸入不可压缩粘性流体中的动力学[8-10]. BALACHANDRAN等[11]通过对上述方程的二阶导数和分数阶导数的简单变换,以及对力学常数取值的适当选择,导出一类分数阶阻尼系统

文献[12]研究分数阶阻尼系统解的存在唯一性. 文献[13]研究带有控制时滞的分数阶阻尼系统的可控性问题.
综上所述,本文将研究如下带有时滞和非局部条件的分数阶阻尼系统:

其中:0<β <1<α <2;表示阶α阶Caputo型分数阶导数;x(·)∈C([-τ,T],Rn)是状态向量,T为给定正实数;φ(·)是给定的初始函数;A ∈Rn×n是常数矩阵;τ >0 是时滞;f:[0,T]×Rn→Rn联合连续函数;n,m:C([0,T],Rn)→Rn是非线性函数且x0,x1是Rn中的元素;若x ∈C([-τ,T],Rn),则xt∈C([-τ,0],Rn)定义为xt(s)=x(t+s),t∈[-τ,0].
解的存在唯一性问题[14-17]是研究系统其他性质的前提,若考虑系统可控性、可观测性、稳定性等问题,则必须先讨论其解的存在唯一性. 而对于含有多分数阶项的分数阶微分方程解的存在唯一性研究要比传统分数阶微分系统复杂很多. 因此,本文将研究含有时滞和非局部初值条件的分数阶阻尼系统(1)解的存在唯一性问题.
1 预备知识
本文中,C([-τ,T],Rn)为由所有从[0,T]映射到Rn的全体连续函数构成的Banach空间,其上范数定义为‖ ‖x=max{ ||x(t):t∈[0,T]}. 记 ||· 为任一向量范数,‖ ‖· 为其诱导的矩阵范数. 下面将介绍本文的基础概念及所需相关引理.
定义1[1]函数f:[0,∞)→R,其下限为0 的α阶分数阶积分的定义如下:

其中Γ(·)是伽马函数.
定义2[1]函数f:[0,∞)→R,其下限为0 的α阶Caputo型分数阶导数的定义如下:
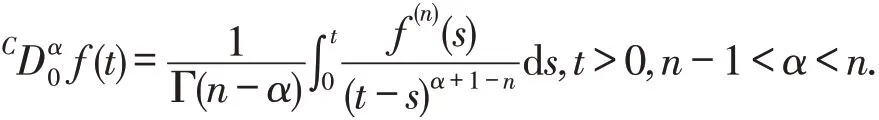
引理1[1]Caputo型分数阶导数有如下性质:

特别地,当1<α <2 时,有

引理2[18]若0<β <1<α <2,则有

2 主要结果
利用压缩映射原理给出系统(1)解的存在唯一性结果. 首先给出系统(1)的等价积分方程,对方程两边进行α阶分数阶积分,则由引理1和引理2可得

在给出结果证明之前,需要先给出以下几个假设条件
(h1)对∀t∈[0,T],x,y ∈Rn,存在一个正常数lf使得

(h2)对∀t∈[0,T],x,y ∈Rn,存在一个正常数lm使得

(h3)对∀t∈[0,T],x,y ∈Rn,存在一个正常数ln使得


另外,为书写方便,记下面给出本文的主要结果.定理1 假设条件(h1)~(h3)成立,若

则系统(1)在[0,T]上存在唯一解.
证明首先定义空间其中

易证Cr是Banach空间. 现定义映射
Step1 ∀x ∈Cr,有Φx ∈Cr. 事实上,任取x ∈Cr,有
由假设条件(h1)~(h3)可知

因对任意的x(·)∈Cr和0 ≤s≤T,有
因对任意的x(·)∈Cr和0 ≤s≤T,有
故由定理条件可知,Φ:Cr→Cr是压缩映射. 由压缩映射原理可知,系统在[0,T]上存在唯一解.
