logistic回归在学生发展方向中的方法与应用
2020-03-20但诗瑶黄文杰石凯
但诗瑶,黄文杰,石凯
(乐山师范学院 数理学院,四川 乐山)
一 文献综述
现今,随着信息社会的飞速发展,工作的类型也越来越多样化,在招生人数不停增加、社会就业竞争激烈的情况下,传统的培养模式会导致学生的就业品质不高,职业的稳定性也不好。这一现象引起了一些学者的注意。在大数据与机器学习飞速发展的时代,已有学者利用了不同方法探寻学生发展方向与各种因素之间的关系。尉建文[1]研究了父母的社会地位与社会资本对大学生求职意愿的影响,发现这两个方面对大学生就业的影响存在很大差异。张杨和王琴[2]发现家庭禀赋和人力资本对大学生出国意愿产生了不同程度的影响。丁彤[3]探究了影响考研的客观因素。陈迎明[4]回顾了大学生就业影响因素十年研究,并将这些因素划分为内部因素和外部因素、单因素和多因素,并指出已有研究对于解决大学生就业问题的期望仍有一定差距。孙笑飞[5]在基于数据分析的高职学生发展趋势预测算法实践中利用了K-Means算法作为学生预测的核心算法,引入判别函数等来对K-Means算法进行改进,开展了对高职学生的发展趋势预测。孙怡帆[6]等人在大学生毕业方向预测中使用机器学习领域的Lasso-Logistic算法,构建了精准度高达70%以上毕业生去向的预测模型。纵观对大学生发展方向的研究,其中对于影响因素的探究较多,而对于预测算法的研究则较少。
本文在基于已有的对大学生发展方向的研究结果中客观选择影响因素,利用机器学习中的logistic回归算法建立并不断训练模型,找寻其中关联度最高的影响因素来建立预测模型,并保证较高的预测精确度。旨在为高校研究大学生发展方向提供一定的参考,为学校和社会寻觅到更适合学生发展的培养方案提供帮助,让高校学生可以正确定位自己。本文所提供的理论参考和预测模型能使院校工作者在进行人才培养工作时有据可依,有利于完成人才培养的目标,提升资源的利用率和办学质量。同时也能为社会制定大学生相关政策提供建议,促进社会发展。
二 logistic回归
(一) 回归分析
回归分析(regression analysis)是一种运用十分广泛的数理统计方法。它主要用于确定两种或两种以上变量间相互影响程度,该方法侧重考查变量之间的数量变化规律。回归分析通过建立回归方程研究变量之间的密切程度,帮助人们寻找隐藏在数据中的统计规律性,明确变量受一个或多个变量的具体影响程度,使得人们对变量间的关系了解得更直观、透彻,并能高效提取出有效信息。对变量进行合理的回归分析,还能为今后的预测提供科学的依据。回归分析预测法是回归分析在变量预测方向上的一个推广,它将建立在变量之间的回归方程作为预测模型,筛选出对因变量产生影响的主要因素,并根据自变量在预测范围内的数量变化来预测因变量在该范围内的结果。
(二) logistic回归模型
回归分析是剖析数据和建模的重要工具,回归模型就是基于回归分析所建立的。当因变量是二分类或多分类型变量时,无法借助一般线性回归模型进行研究。因为它不能满足一般线性回归模型对因变量取值的要求,且违反了回归模型的前提假定,如不再满足同方差。因此,当因变量为定性变量时,采用logistic回模型。当因变量为二分类变量时,采用二项logistic回归模型;当因变量为多分类变量时,采用多项logistic回归模型。
1、二项logistic回归模型
当因变量为二分类变量时,无法采用一般线性回归模型进行分析。可以对因变量做一些变换,使它满足一般线性回归模型建模的要求。一元线性回归模型的可表示为后者是对当自变量为x1i时因变量均值的预测。对于二分类因变量来说,就是当自变量为 x1i时因变量为1的概率的预测。此时,一元线性回归方程的一般形式可写为:
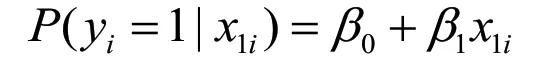
概率P在此处并不满足一般线性回归模型对因变量取值的要求,需要对P采取合理的变换。变换后的P需要同时满足实际取值范围在 ~+−∞ ∞之间且与自变量之间的关系是非线性,即回归函数应该是限制在区间[0,1]内的连续曲线。常常采用Logit变换对P进行处理来解决该问题。
首先引入逻辑斯蒂函数(logistic distribution)概念[7]。
逻辑斯蒂函数取值范围为(0,1),它由下列公式定义:
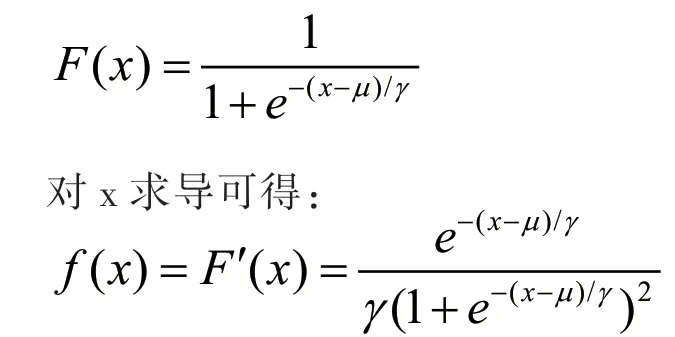
其中,µ和γ分别为位置参数和形状参数(γ>0)。
逻辑斯蒂函数的图像形如S形曲线,所以又称为sigmoid函数。二项logistic回归模型是一种分类模型,由条件概率分布 P( x| y )表示,形式即为参数化的逻辑斯蒂分布。

图1 logistic函数图像
图2 logistic密度函数图像
可以看出,在线性回归模型中引入逻辑斯蒂函数可以使概率P满足一般线性回归模型对因变量的取值要求。引入Logit变换:
一件事件的几率(Odds,也称为优势)是指该事件发生的概率与改时间不发生的概率的比值[2]。如果事件发生的概率是P,那么该事件的几率是,该事件的对数几率(log odds)或logit 函数是

以上对P作的两步变换即为Logit变换,并且logit( p) 往往和自变量呈线性关系。我们可利用一元线性回归模型写出 logit( p ) 与自变量的多元分析模型:
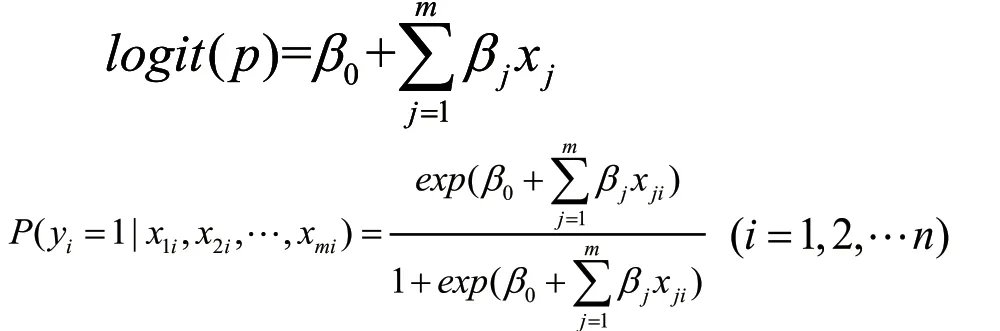
其的中 第 xji表个示观第测j值个,自 β变j量则,为x第ji表j个示自第变j量个所自变对应的回归系数。以上即为二项logistic回归模型。
2、多项logistic回归模型
当因变量为多分类变量时,采用多项logistic回归模型。多项logistic回归模型又分有序和无序。
以包含3个水平的因变量为例介绍有序多项logistic回归模型。假设因变量取值分别为1、2、3,所对应的概率分别为 p1、 p2、 p3,且按照拟合二项logi stic回归模型的步骤,对自变量拟合2个模型:
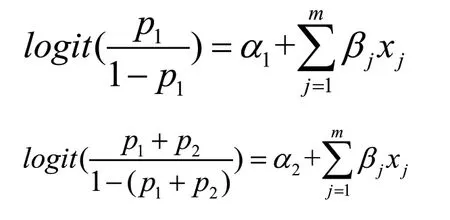
易知模型中自变量所对应的系数 jβ并不改变,改变的只是常数项α。
同理可写出无序多项logistic回归模型:

模型中 ijβ表示第i个模型中第j个自变量所对应的回归系数。大量研究表明,分类数据利用该模型建模效果很好。
(三) 参数估计


对logistic回归对数似然方程的求解,常采用梯度下降法。
三 研究设计
(一) 数据来源
本研究以四川乐山某高校本科院校毕业大学生为研究对象,旨在探索毕业大学生的在校状况与个人发展方向的关系,建立模型,为在校大学生选择发展个人方向提供参考。数据主要由学校各学院、各部门的负责人所提供。数据包括毕业生的性别、籍贯、政治面貌、家庭户口、家庭月收入、进出图书馆次数、学分加权平均分、是否师范类、是否贫困生。
所调查的院校是一所师范类本科院校,调查对象主要是该院校刚毕业的大学生,通过数据整理分析可得出:毕业后选择做教师的学生则占总体学生的52.8%,选择就业的学生占总体学生的28.0%,而选择读研的学生占总体学生的19.2%。样本中女生占了总体的77.6%,男生则有22.4%;女生中毕业后选择教师的占55.2%,选择就业的占23.2%,选择读研的则占21.6%;男生中毕业后选择教师的占44.4%,选择就业的占44.4%,选择读研的则占11.1%。样本中专业是师范类的占总体的74.5%,非师范类的则占25.5%;师范类中选择教师的占68.4%,选择读研的占23.3%,选择就业的占8.3%;非师范类中选择就业的占85.4%,选择读研的占7.3%,选择教师的占7.3%。对数据进行简单分析可得出,女性比男性更愿意选择继续深造;师范类专业的毕业生近七成会选择做教师工作,而非师范类专业的毕业生八成选择毕业后直接就业;可见,是否师范类对毕业生选择发展方向影响显著。

表1 数据情况
(二) 变量说明
本文在归纳和整理研究大学生发展方向影响因素的相关文献后,结合调查院校的实际情况,对学生的综合素质、家庭情况、学业水平进行了分析。最终选取了3个显著的自变量拟合模型。其中是否师范类为定性变量,学分加权平均分、图书馆进出次数为定量变量。因变量是毕业大学生所选发展方向,为定性变量,取值为就业、教师、研究生。

表2 变量摘要
(三) 模型分析
根据所取得的数据,建立无序多项logistic回归模型进行分析。假设模型如下:


本文运用SPSS 23.0软件进行logistic回归分析。利用这三个自变量建立与毕业去向的无序多项logistic回归模型:

表3 模型拟合信息
表3是对模型进行似然比检验的结果,检验的原假设是所有自变量偏回归系数全为0,从反馈结果可看出,自由度为6,显著性 p< 0.001,则应该拒绝原假设,表明至少有一个偏回归系数不为0。

表4 似然比检验
从表4中的检验结果可以看出,自变量显著性p均小于0.05,则偏回归系数不为0,说明模型中引入的自变量是有统计学意义的,对模型的贡献均为显著的,引入合理。拟合出的模型分别为:
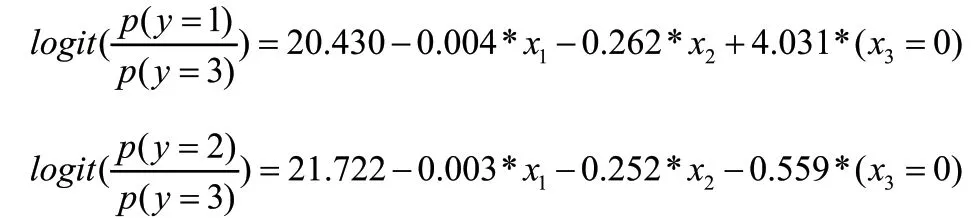
其中 3( 0)x= 表示当学生专业不是师范类时取值为1,反之则为0。
对于logistic模型拟合优度的测量,崔党群[9]曾在相关文献中提出一种方法,他阐述了logistic曲线回归方程因含有回归参数a、b和常量 K,不适宜用一般曲线回归的假设测验方法进行拟合优度检验,并提出可以利用实际值和预测值,运用适合性 χ2测验,进行拟合优度检验。
将模型预测值与实际值进行 χ2检验:
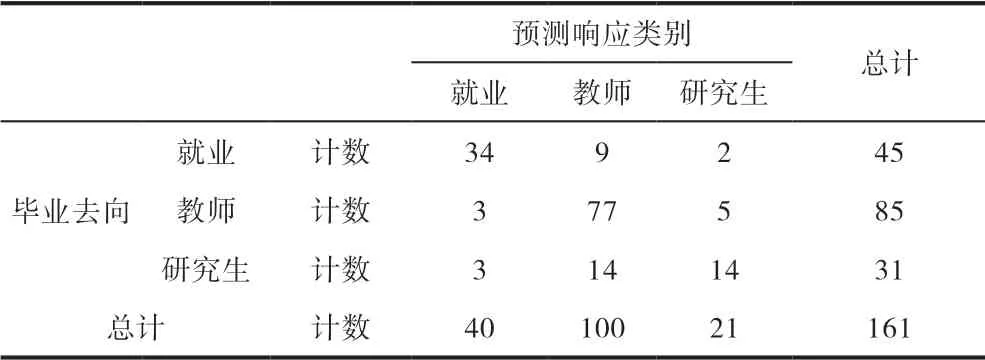
表5 毕业去向交叉表
从表5中可以看出,仅有一个单元格的期望频数小于5,并不超过整个单元格数量的百分之二十,可以使用卡方检验进行分析。

表6 卡方检验
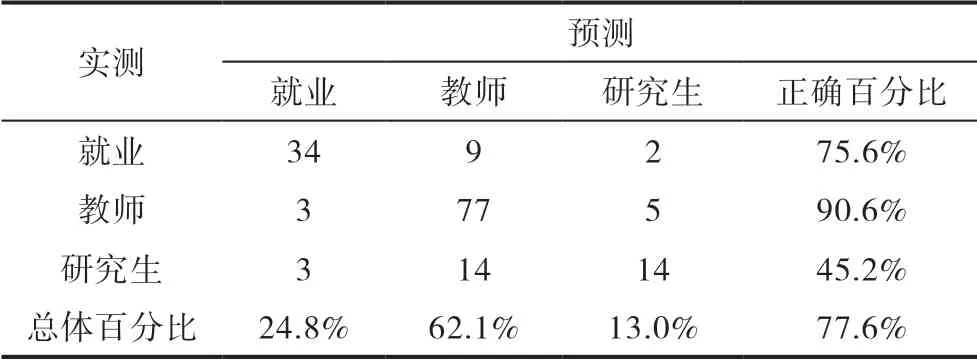
表7 模型预测情况
从表7返回的预测结果得出,拟合的模型对样本预测的正确率为77.6%,效果较好。
(四) 模型预测
本文使用R语言中的nnet包对模型的预测效果进行分析。对样本进行500次随机抽样,每一次按照7:3的比例划分为训练集和测试集。利用训练集拟合无序多项logistic回归模型,将测试集数据代入模型并计算出模型的预测正确率。对每次计算出的预测正确率求和取均值,得到模型的平均预测正确率为76.7%。结果表明无序多项logistic回归模型对大学生发展方向的预测具有较高准确率。
四 研究结论与对策建议
从调查结果可以看出,学生的籍贯、政治面貌、家庭户口、家庭月收入以及是否贫困生对学生选择个人发展方向并无显著影响。在普通师范类本科院校中,学生的考研率并不高,只占了总体学生的两成。其中学分加权平均分与进出图书馆次数对学生发展方向有着正向影响。即分数越高、进出图书馆次数越多的学生更倾向选择继续深造。非师范类的学生在选择继续深造与直接就业中更倾向于毕业直接就业,师范类的学生在这两者中更倾向于选择继续深造。Logistic回归模型在对大学生发展方向的研究中拟合效果显著,预测正确率较高,本文可为相关研究提供一定参考。
对于本科学生来说,在师范类院校选择当教师的学生较多,在该环境下一些非师范类的学生也会选择当教师,这时就需要同学认真思考自己,结合自身兴趣、家庭等因素考虑发展方向,通过网络数据库可以得到研究生的平均薪资会高一些,因此大部分同学可以继续深造,提高生活水平和自身专业素质。对于本科院校来说,本科专业为师范类的同学毕业去向大多是当老师,选择深造的同学较少,在当今社会,本科出身达不到一些中学当教师的要求,院校在早期培养学生时,要多注重学生专业基础,提高学生的学习自主性。并可适当鼓动同学继续深造,提高学历、丰富自身涵养。考研率增加也会使得院校口碑变好,引进更优秀的学生团队与教师团队。在利用本文分析各学生的自身定位后,可以根据学生定位进行资源的分配,提高资源的利用率。对于社会来说,提高国民专业素质是有利于社会发展的,国民素质越高,社会发展越有利,可适当讨论扩招方面的政策,提高国民专业素质,但同时还要考虑社会竞争关系,扩招幅度应循序渐进,不宜过大导致研究生综合水平降低。
