网络环境下切换模糊时滞系统的非脆弱控制

刘 毅,梅玉鹏,李国燕,潘玉恒

(天津城建大学 计算机与信息工程学院,天津 300384)

0 概述

网络控制系统(Networked Control System,NCS)是由网络形成的闭环反馈控制系统。在该类系统中,传感器、控制器与执行器的数据传输都是通过网络实现的[1-2]。NCS不仅能节省系统设计成本,还使得远程信息资源共享成为可能,其可维护性和灵活性强,在工业控制网络、无人机等领域应用广泛,是控制系统的一个发展方向,具有重要的研究价值[3-5]。

网络切换控制系统是NCS中十分重要的一种类型。研究者利用切换系统理论对网络控制系统进行分析,取得了较多的成果[6-8],其中采用平均驻留时间法设计系统的切换律,受到了许多学者的关注[9-11]。文献[12]采用平均驻留时间法研究了网络控制系统的丢包和时延问题,给出系统指数稳定的条件。文献[13]采用平均驻留时间法对网络切换系统的故障检测等问题进行研究,并结合李雅普诺夫函数理论,给出系统的稳定条件。文献[14]采用平均驻留时间法研究了存在双边时变时延的网络控制系统指数稳定问题。但上述文献均未考虑系统非线性的情况,而在现代工业过程中存在严重的非线性,因此,研究非线性网络切换系统的稳定性问题具有重要价值。目前,采用T-S模型建模并结合平均驻留时间法分析该类系统稳定控制问题的研究成果较少。

随着现代工业过程的日趋复杂,在实际的切换模糊控制系统中,不可避免地存在着控制器参数摄动[15],并且普遍存在时滞[16]。为此,文献[17-18]研究了网络控制系统的非脆弱控制问题,文献[19-20]针对系统中存在的时滞问题进行了研究。控制器参数摄动、系统参数不确定和时滞是造成系统不稳定的一个主要原因。文献[21]针对带有时滞的不确定切换模糊系统的非脆弱控制问题,运用李雅普诺夫函数法设计系统切换律,并给出了系统渐近稳定的条件。

本文在文献[21]的基础上,考虑系统存在时变时滞及网络时延的情况,通过运用平均驻留时间法、李雅普诺夫稳定性定理及线性矩阵不等式,得到NCS中的切换律、控制器的设计方法和使系统指数稳定的平均驻留时间条件。

1 问题描述

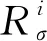
x(k+1)=(Aσi+ΔAσi)x(k)+

(Adσi+ΔAdσi)x(k-d(k))+

(Bσi+ΔBσi)uσ(k)+

(Bdσi+ΔBdσi)uσ(k-1)

x(k)=Ψ(k),k∈[-d,0],i=1,2,…,Nσ

(1)

假设1不确定矩阵是模有界的,即:

(2)

结合PDC算法,由单点模糊化、乘积推理和平均加权反模糊化,系统(式(1))可表示为:

(Adσi+ΔAdσi)x(k-d(k))+(Bσi+ΔBσi)uσ(k)+

(Bdσi+ΔBdσi)uσ(k-1)]

(3)

其中,切换信号σ可以由函数vσ(x(k))来刻化。当切换信号传递到子系统时,vσ(x(k))=1,反之vσ(x(k))=0。

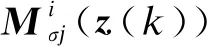
设计模糊状态反馈控制器形式如下:

(4)

其中,Kσi表示控制增益矩阵,ΔKσi表示控制增益摄动矩阵。

假设2控制器增益摄动满足:

ΔKσi=HσiRσi(k)Gσi

将式(4)代入式(3),可得:

μσj(z(k))[(Aσi+ΔAσi)x(k)+(Adσi+ΔAdσi)×

x(k-d(k))+(Bσi+ΔBσi)(Kσj+ΔKσj)x(k)+

(Bdσi+ΔBdσi)(Kσj+ΔKσj)x(k-1)]=

(5)

其中:

网络控制系统要达到指数稳定,切换信号σ需满足平均驻留时间条件。

定义1[22]若存在标量δ>0以及0<γ<1,使得‖x(k)‖≤δγ(k-k0)‖x(0)‖,k≥k0≥0,则网络切换模糊时滞系统(式(1))在切换信号σ作用下是指数稳定的,γ表示衰减率。

定义2[23]对于任意时刻t2>t1>0,以Nσ(t1,t2)表示时间段[t1,t2]上的切换次数,若存在Tα>0,N0≥0使式(6)成立,那么常数Tα为平均驻留时间,N0是抖振界,本文取N0=0。

(6)

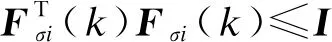
2 理论推导

定理1假设有正定对称矩阵Pσ,Sσ,Qσ和矩阵Kσi,常数λ∈(0,1),μ∈[1,+)及ε≥0使得:

(7)

Vσ(ki)≤μVσ(kj),∀i,j∈M

(8)

并且,切换信号满足平均驻留时间:

(9)

那么,系统(式(1))是指数稳定的,并且系统状态估计为:

在式(7)～式(9)中:

θ1=-4(1-λ)Pσ+4Sσ+4(1-dM-dm)Qσ+

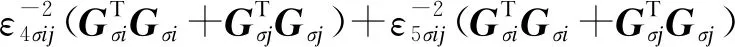
(BσjHσi)(BσjHσi)T]

Ξ1=Aσi-BσiKσj+Aσj-BσjKσi

(BdσiHσj)(BdσiHσj)T]

其中,*是对称位置矩阵的转置。

证明对于第σ个子系统,选取时滞依赖的Lyapunov-Krasovskii泛函为:

(10)

其中:

V1σ(x(k))=xΤ(k)Pσx(k)

V4σ(x(k))=xΤ(k-1)Sσx(k-1)

由式(10)可知,存在2个正数ξ1、ξ2使得:

ξ1x2≤Vσ(x(k))≤ξ2x2

(11)

其中:

记Lyapunov函数的差分为ΔVσ(k),则对于V1σ(x(k))的差分,有以下公式:

ΔV1σ(x(k))+λV1σ(x(k))=

V1σ(x(k+1))-(1-λ)V1σ(x(k))=

xT(k+1)Pσx(k+1)-(1-λ)xT(k)Pσx(k)

(12)

由引理1可得:

(13)

其中:

对于V2σ(x(k))的差分,有以下公式:

ΔV2σ(x(k))+λV2σ(x(k))=

V2σ(x(k+1))-(1-λ)V2σ(x(k))=

(1-λ)d(k)xΤ(k-d(k))Qσx(k-d(k))

(14)

由上式可知:

(15)

由此可得:

ΔV2σ(x(k))+λV2σ(x(k))≤

(1-λ)dMxΤ(k-d(k))Qσx(k-d(k))

(16)

对于V3σ(x(k))的差分,有以下公式:

ΔV3σ(x(k))+λV3σ(x(k))=

V3σ(x(k+1))-(1-λ)V3σ(x(k))=

(1-dm-2+dM+1)xΤ(k)Qσx(k)-

(17)

对于V4σ(x(k))的差分,有以下公式:

ΔV4σ(x(k))+λV4σ(x(k))=

V4σ(x(k+1))-(1-λ)V4σ(x(k))=

xΤ(k)Sσx(k)-xΤ(k-1)Sσx(k-1)

(18)

结合式(12)～式(18)可得:

ΔVσ(x(k))+λVσ(x(k))≤

(19)

其中:

Ω=-4(1-λ)Pσ+4Sσ+4(1+dM-dm)Qσ

Φ222=Φ122-4(1-λ)dMQσ

Φ233=Φ133-4Sσ

由式(19)可知,若式(20)成立,则ΔVσ(x(k))+λVσ(x(k))<0成立。

(20)

应用Schur分解方法,式(20)可化为:

(21)

其中:

(22)

其中:

(23)

以上推导说明,在满足式(7)的条件下:

Vσ(x(k+1))-Vσ(x(k))+λVσ(x(k))≤0

即:

Vσ(x(k+1))≤(1-λ)Vσ(x(k))

(24)

由式(8)和式(24)可得:

Vσ(x(k))≤(1-λ)(k-k0)μ(k-k0)/TαVσ(0)=

((1-λ)μ1/Tα)(k-k0)Vσ(0)

(25)

由式(11)和式(25)可得:

ξ1‖x(k)‖2≤Vσ(x(k))≤((1-λ)μ1/Tα)(k-k0)×

Vσ(0)Vσ(0)≤ξ2‖x(0)‖2

则指数稳定的状态估计为:

(26)

因此,根据式(9)和式(26)可得γ<1,系统(式(1))在所设计的切换律下是指数稳定的。

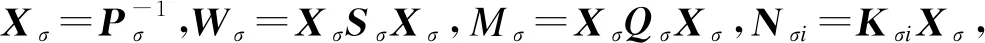
X1*********GσiXσ-ε24σijI********GσjXσ0-ε24σijI*******GσiXσ00-ε25σijI******GσjXσ000-ε25σijI*****E1σiXσ-E2σiNσj0000θ2****E1σjXσ-E2σjNσi00000θ3***Λ000000X2**00000000-4(1-λ)dMMσ*00000000E3σiXσ-ε22σijI00000000E3σjXσ000000000AdσiXσ+AdσjXσ000000000000000000000000000000000000000000000000000000000000000000000000000000000→←****************************************************************************************************-ε22σijI*********0-13Xσ+ε22σijD-********00-4Wσ*******00GσiXσ-ε26σijI******00GσjXσ0-ε26σijI*****00GσiXσ00-ε27σijI****00GσjXσ000-ε27σijI***00E4σiNσj0000θ7**00E4σjNσi00000θ8*00-BdσiNσj-BdσjNσi000000X3<0(27)

X1=-4(1-λ)Xσ+4Wσ+4(1-dM-dm)Mσ

(BσjHσi)(BσjHσi)T]

(BdσiHσj)(BdσiHσj)T]

Λ=AσiXσ-BσiNσj+AσjXσ-BσjNσi

3 仿真实验

本文通过2个仿真实验来验证本文方法的有效性。

实验1对于如下不确定网络切换模糊时滞系统:

(Adσi+ΔAdσi)x(k-d(k))+(Bσi+ΔBσi)uσ(k)+

(Bdσi+ΔBdσi)uσ(k-1)]

其中:

取隶属度函数:

μ11(x1(k))=μ12(x2(k))=1-1/(1+e-4x1(k))

μ21(x1(k))=μ22(x2(k))=1/(1+e-4x1(k))

选取初始点[0.3,-0.1]Τ,利用MATLAB仿真,系统状态曲线如图1所示,其切换信号如图2所示。由仿真结果可知,在本文所设计的切换律和控制器下,系统是指数稳定的。文献[21]中,取时滞时间d=1,系统状态曲线如图3所示。

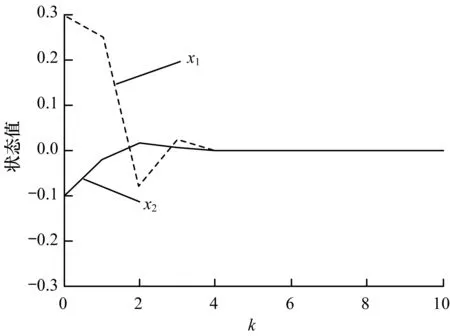
图1 网络切换模糊系统的状态曲线

图2 网络切换模糊系统的切换信号

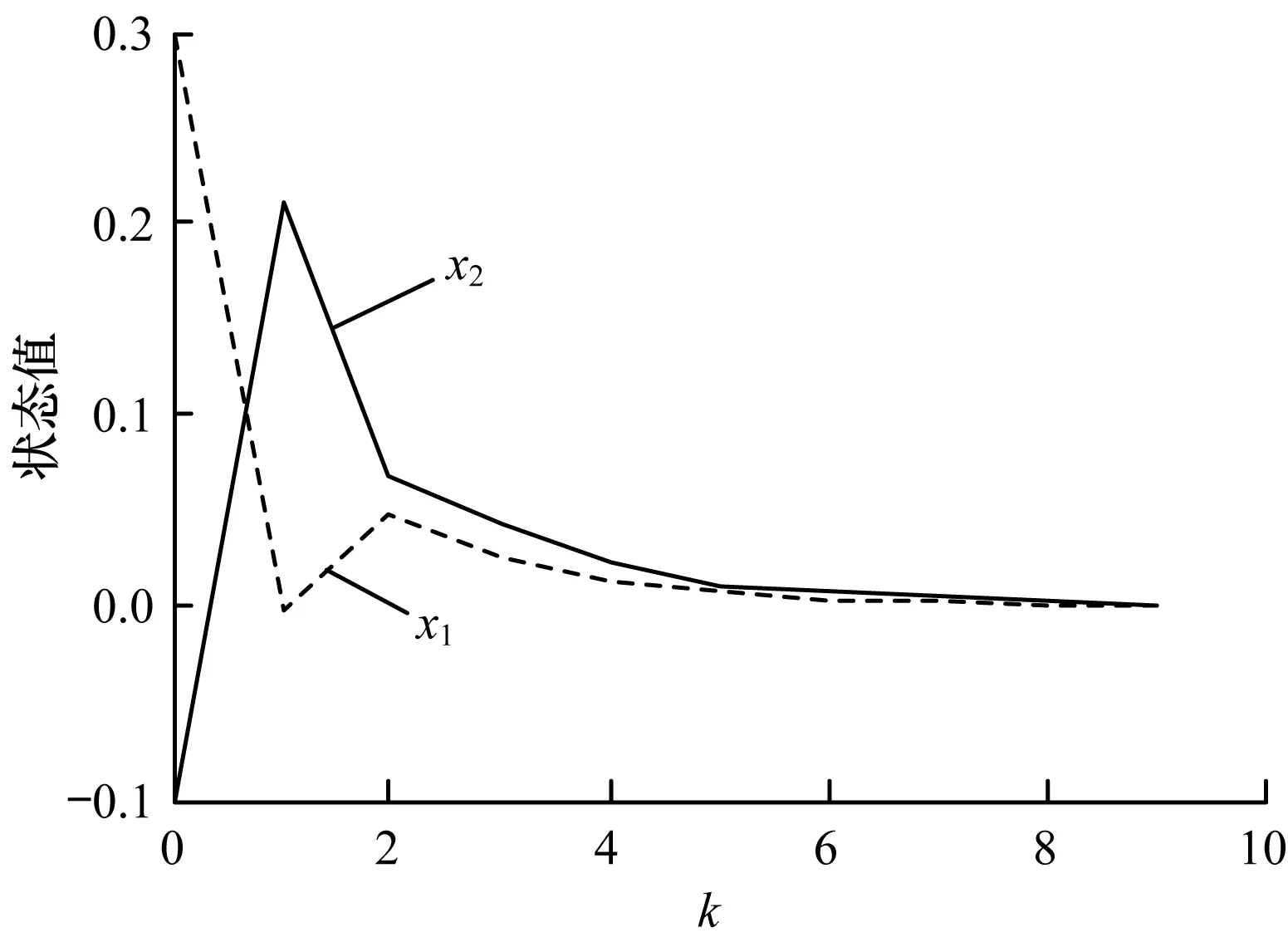
图3 采用文献[21]方法的系统状态曲线

Fig.3 State curve of network switched fuzzy system using the method in Ref.[21]

本文选取的时滞1≤d≤4,文献[21]中的时滞d=1,因此,本文中的时滞不小于文献[21]中的时滞。由图1和图3可知,即使本文考虑了系统存在网络时延和时变时滞的情况,系统的收敛速度依然比文献[21]中系统的收敛速度快。由此可知,采用平均驻留时间法设计系统的切换律,系统收敛速度更快,性能指标更好。

实验2针对图4所示的倒立摆系统,根据牛顿力学定律,建立系统的动态方程(不计倒立摆系统中的各种摩擦力):

其中,x1为摆与垂直线的夹角,x2是角速度,g=9.8 m/s2是重力加速度,a=1/(m+M),摆的质量m=2 kg,车的质量M=8 kg,摆的长度l=0.5 m,u为作用于小车的力。

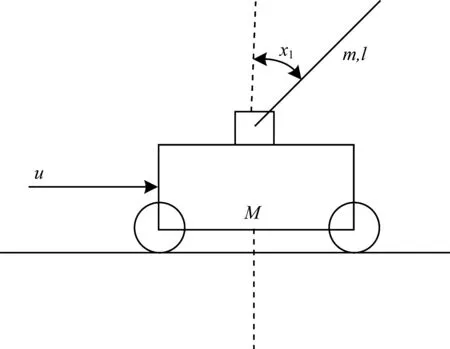
图4 倒立摆系统

假设x1受时滞干扰,将摆角范围[-30°,30°]分成2个区域R1和R2,区域R1为15°<|x1|≤30°,区域R2为|x2|≤15°,分别建立2个模糊子系统,并得网络切换模糊时滞系统模型:

[(Aσi+ΔAσi)x(k)+(Adσi+ΔAdσi)x(k-d(k))+

(Bσi+ΔBσi)uσ(k)+(Bdσi+ΔBdσi)uσ(k-1)]

其中:

当|x1|≤15°时,取隶属度函数为:

μ21(x1(k))=1-|x1(t)|/15

μ11(x1(k))=|x1(t)|/15

当15°<|x1|≤30°时,取隶属度函数为:

μ21(x1(k))=|x1(t)|/15-1

μ11(x1(k))=2-|x1(t)|/15

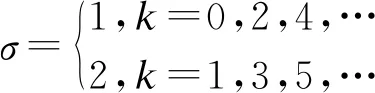
选取初始角度为x1(0)=25°,x2(0)=0,利用MATLAB仿真,系统的状态曲线如图5所示,其切换信号如图6所示。由仿真结果可知,在本文所设计的切换律下,系统是指数稳定的。

图5 倒立摆系统的状态曲线

图6 倒立摆系统的切换信号

4 结束语

本文针对带有时滞的网络切换模糊系统,采用平均驻留时间法,选取合适的李雅普诺夫函数,设计了系统切换律并完成控制器的求解,给出时滞相关的网络切换模糊系统指数稳定的条件。仿真结果表明,与文献[21]中的李雅普诺夫函数法相比,采用平均驻留时间法设计系统的切换律,可有效加快系统收敛速度,优化指标性能。下一步将在本文研究的基础上对系统的H∞控制和故障检测问题进行分析。