基于E-t-SNE的混合属性数据降维可视化方法

魏世超，李 歆，张宜弛，周晓锋，李 帅

1.中国科学院 沈阳自动化研究所，沈阳110016

2.中国科学院大学，北京100049

3.中国科学院 网络化控制系统重点实验室，沈阳110016

4.中国科学院 机器人与智能制造创新研究院，沈阳110016

1 引言

现实生活中的大量数据通常包含可能对决策者有用的隐藏模式，但这些数据通常维度较高。例如，在入侵检测、欺诈检测、医疗分析领域[1]的数据，通常包含数百维。模式识别、图像处理[2]领域的数据通常包含上千个特征。现实数据高维特性的存在带来了计算成本增加、维度灾难[3]等问题，不利于对数据的理解分析。解决数据高维特性问题的一种方法是降维，即寻求减少数据特征数量的技术。

众多研究者提出了多种降维技术。一种是基于特征选择的方法，根据一些标准选择原始特征的子集[4]。Danubianu 等人[5]提出了一种应用相关性的筛选器来寻找相关特征的特征选择方法。另一种降维技术是基于特征变换的方法，通过指定的变换函数将高维数据映射到低维空间。与特征选择方法不同，生成的特征集不是原始特征的子集，而是根据原始特征新创建的。目前基于特征变换的降维方法主要有主成分分析（PCA）[6]、局部线性嵌入（LLE）[7]、等距映射（Isomap）[8]、局部切空间排列（LTSA）[9]、随机近邻嵌入（t-SNE）[10]、拉普拉斯特征映射（LE）[11]等。这些方法已经被应用于多个领域。Jamieson等人[12]将拉普拉斯特征映射和t-SNE应用于计算机提取的乳腺癌特征空间中，对医学图像映射进行分类和可视化检查。Garces等人[13]运用t-SNE将不同风格的剪切画可视化。Liu等人[14]采用LLE对肿瘤基因表达数据进行降维。

以往研究的不足之处在于研究都是在数值数据的背景下进行的。然而大多数真实世界的数据集同时包含分类属性和数值属性。例如，信用系统的数据包括年龄、年薪、储蓄金额等数值属性，以及教育背景、职业、婚姻状况等分类属性[15]。许多知识发现算法并不能处理混合类型数据。这些算法只分析数值或分类数据，并通过将一种类型的数据转换为另一种类型的数据来解决这一缺陷。对于只处理数值型数据的算法，独热编码（One-Hot Encoding）是一种普遍采用的方法，它将每个分类值转换为二进制向量。然而这种方法有几个显著的缺点。首先，转换后的数据增加了维度，计算成本也随之增加，其次将分类属性转换为二进制向量，未考虑属性间的相互关系，造成数据语义丢失，影响后续的分类聚类等算法的精度和性能。

本文主要针对t-SNE 算法不能处理混合数据的缺点，提出一种E-t-SNE 算法扩展其对混合属性数据的处理能力。该算法引入信息熵的概念，考虑不同分类属性值对距离计算过程中不同的贡献程度，然后采用与数值属性加权结合的方式，构造混合属性数据的距离矩阵。为了验证该算法处理混合属性数据的有效性，采用k 近邻(kNN,k-Nearest Neighbor）[16]分类算法验证降维后数据的分类精度优于其他距离度量方案。此外，将混合属性数据投影到低维空间进行可视化，证明了该算法对混合数据集的可视化展示更符合人们对数据的直观理解。

2 相关定义

2.1 t分布随机近邻嵌入算法

高维数据降维可视化处理是将维数大于3 的数据转换为2 维或者3 维，降维后的数据能够在低维空间可视化展示并可以用于后续的机器学习算法。Hinton 及Roweis[17]于2002 年提出了一种随机近邻嵌入（SNE）降维方法。由于SNE 方法的价值方程优化困难并且存在低维数据拥挤问题，因此Maaten 及Hinton 于2008 年在SNE 的基础上提出基于t 分布的随机近邻嵌入方法（t-SNE）。t-SNE的思想是在低维空间中采用重尾t分布构造一个概率分布，使其在高维空间中构造的概率分布相似。在概率分布中，相似的数据点被选中的概率较高，不相似的数据点被选中的概率较低。高维空间中，点j相对于点i的概率分布定义为：

其中，σ 是以xi为中心的高斯函数的方差，由二进制搜索算法确定。设高维空间中的联合概率pij为对称条件概率，即

其中，n是数据点的个数。对于高维数据xi和xj在低维空间中的映射yi和yj，采用自由度为1 的t 分布表示低维联合概率分布，即

为保证低维空间映射点之间的联合概率分布qij较好地模拟高维空间数据点之间的联合概率分布pij，采用梯度下降法最小化所有数据点的KL 散度（Kullback-Leibler divergences）得到低维空间最佳模拟点。目标函数C 和梯度下降法优化的定义如下：

为了加速优化过程，避免陷入较差的局部最小值，在梯度中加入一个动量项：

2.2 独热编码

独热编码（One-Hot Encoding）是机器学习算法中处理分类属性数据的常用方法。由于很多现实世界中的数据集不总是连续的数值型数据，在应用回归、分类、聚类等机器学习算法时，数据集中包含的分类型数据无法直接进行距离和相似度计算。独热编码将具有k 个不同值域的分类属性转换为一组k 个二进制属性，每个二进制属性都对应于k个分类值中的一个。

然而这种对分类属性数据的处理方式缺点显著。首先转换后的数据大大增加了数据维度，计算成本增加。其次，将分类属性转换为二进制向量，未考虑属性间的相互关系，造成数据语义丢失，影响后续的分类聚类等算法的精度和性能。

2.3 k 近邻分类算法

k 近邻(kNN,k-Nearest Neighbor）分类算法是最常用的分类算法之一，被应用于数据挖掘、模式识别等多个领域。算法采用k 个最近邻居的类标签来确定未知点的类标签，即k 个最近邻文本中大多数属于某个类别，则样本也属于这个类别，故k 值的选取至关重要。如果k 值偏小，会提高噪声的干扰；如果k 值偏大，并且测试样本中属于训练集中包含数据较少的类，则会增加噪声，降低分类准确性。

3 E-t-SNE混合属性数据降维可视化方法

观察式（1）可以发现，t-SNE算法将高维数据点间的欧式距离转换为表示相似性的条件概率[18]，常用的空间距离计算方法欧式距离并不适合处理分类型数据。本文采用一种新的距离计算方法，分别构建数值型数据的距离矩阵和分类型数据距离矩阵，然后将两个矩阵融合得到混合数据的距离矩阵，输入t-SNE 算法进行降维并可视化。

3.1 距离矩阵度量

关于混合属性数据的公式符号描述如下[19]：X={ x1, x2,…,xn} 表示N 个混合数据对象的数据集，对于 每 一 个 xi(1 ≤i ≤n),混 合 型 数 据 集 xi代 表M(M=Mn+Mc)个属性其中表示Mn个数值型数据，表示Mc个分类型数据。表示数值部分的第k 个属性，表示分类部分的第k 个属性。第k 列分类属性的定义域表示为表示分类属性的个数。

3.1.1 数值型数据的距离矩阵

D(n)是一个n×n(n=N)的矩阵，对角线上元素全是0，表示数据点自身与自身的距离，表示和之间的距离，

3.1.2 分类型数据的距离矩阵

传统的定义分类属性数据之间距离的方式是建立在每个分类属性权重相同的情况下，数据相同距离为0，不同距离为1。本文表示为公式如下：

这种定义分类属性数据的方法忽略了不同分布的不同属性值对距离计算时贡献度的差异。因此，为了考虑贡献度的差异，为分类属性加入权重wk，公式（9）可修改为：

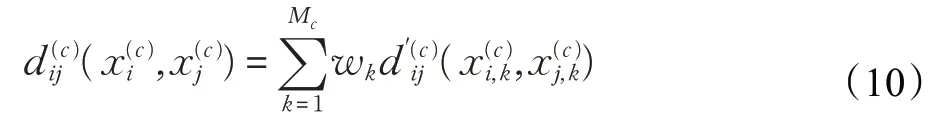
显然wk是分类属性的权重，它表示对分类属性距离计算时的贡献程度。这里

然后讨论每个分类属性权重wk的计算方式，本文引入信息熵的概念计算权重[20]。由信息熵的性质可知，信息熵可以作为一个系统复杂程度的度量，如果系统越复杂，出现不同情况的种类越多，那么他的信息熵就越大，反之一个系统越简单，出现情况种类越少，信息熵越小。同理，如果数据集中分类型数据的定义域中ak,t种类越多，分布越不均匀，则的信息熵越大，即对距离的计算贡献程度越高，权重越大。因此的信息熵可表示为：

这里p(ak,t)是分类属性中ak,t的概率：

其中，rk为中分类值的数量。因此，数据集中分类属性对距离计算时贡献程度可用权重wk表示：

将式（14）代入式（10）中，得到分类属性数据的距离计算公式：

2.依规处理国际税收协定与国内税法的对接关系。双边或多边税收协定属于国际法的范畴。双边税收协定是由缔约国双方政府谈判后达成的，经过各自国家的立法程序后生效的，因此对于缔约国政府具有法律上的约束力。

D(c)是一个n×n(n=N)的矩阵，对角线上元素全是0，表示数据点自身与自身的距离表示和之间的距离，

3.1.3 混合型数据的距离矩阵

根据以上内容可以发现，对于混合型数据集的距离计算采用数值型和分类型分别计算的方法。数值型数据点直接采用欧式距离进行度量，分类型数据点引入信息熵的概念，将不同分类属性对距离计算的贡献程度量化成权重，用权重与分类值之间距离相乘的方法构造出分类属性数据点之间的距离。

最后将计算出来的数值型数据点之间的距离与分类型数据点之间的距离相加，得到混合属性数据点之间的距离dij(xi,xj)，表示为：

3.2 算法实现

E-t-SNE算法流程如图1所示。

图1 E-t-SNE算法流程

E-t-SNE 算法描述如下所示，其中迭代次数T 太小容易导致优化过程不完全，太大增加算法执行时间，本文设置为1 000；较大的动量项可以使优化过程避免陷入较差的局部最优，根据经验，当迭代次数T ＜250 时，动量项α(T)=0.5，当T ≥250时，α(T)=0.8；学习率η初值为100，每次迭代结束根据自适应学习率机制进行更新；维数m 设置为2[21]。

算法1E-t-SNE算法

（1）分别根据式（7）和式（15）构建数值型数据距离矩阵D(n)和分类型数据距离矩阵D(c)；根据公式（17）构建混合数据距离矩阵D；

（2）分别根据式（1）和（2）计算pj|i和pij；

（3）初始解Y(0)={ y1, y2,…,yn} 采样与正态分N(0,10-4I)

（4）for t=1 to T

①根据式（3）计算qij；

②根据式（5）计算梯度；

③根据式（6）计算Y(t)；

（5）得到低维数据表示Y(T)={ y1, y2,…,yn}。

输出：混合数据集在低维空间的数据表示。

4 实验分析

4.1 实验数据集和评价方法

为了验证E-t-SNE 算法的有效性，本文选用UCI 机器学习知识库中的4个真实混合数据集：Credit Approval、Australian Credit Approval、Heart、Adult。数据集Credit Approval 包含2 个类，6 个数值属性和8 个分类属性，共653条数据；数据集Australian Credit Approval包含2个类，6个数值属性和9个分类属性，共690条数据；数据集Heart 包含2 个类，7 个数值属性和6 个分类属性，共270条数据；数据集Adult包含2个类，3个数值属性和3个分类属性，共1 100 条数据。表1 列出了4 个数据集数据量，数值属性个数，分类属性个数以及类的个数。

表1 混合型数据集的详细信息

为了评价E-t-SNE 算法的性能，本文使用了4 个真实混合数据集。由于不知道数据在高维空间中的结构，所以无法通过对比高维和低维空间投影映射的方法来直接的评估性能。E-t-SNE算法本身是一种混合数据降维可视化算法，按照理论，降维以后的数据应该保留了原始高维空间中数据集的分类特征。因此，可以对混合数据集降维之后的数据进行评价，验证此降维可视化算法对后续数据分析的影响。本文采用k 近邻(kNN)分类算法，将降维以后的数据中80%用做训练集，20%做测试集，通过对测试数据分类准确度的比较，对本文E-t-SNE 算法和独热编码方式、余弦距离度量方法进行了评价。

4.2 实验结果分析

为验证E-t-SNE 算法的有效性，本文采用多种距离计算方法构建混合数据集的距离矩阵，并与本文算法对比。其中独热编码方式是将分类属性转换为k 个二进制属性构建距离矩阵；余弦距离方法是将混合属性数据转换为向量，通过计算向量间夹角的余弦值构建距离矩阵。原始的t-SNE 算法不能直接处理混合数据集，但是本文将混合数据集不做处理直接输入t-SNE 算法，作为对比降维以后分类准确率的基准，以凸显本文算法的有效性。

文献[10]指出，t-SNE 算法的性能对困惑度Perp 变化较为敏感。根据Perp 的定义，若Perp 太小，则低维嵌入点孤立，看不到低维空间中的聚簇效果；若Perp太大，则所有低维嵌入点聚集成一个簇，无法辨析数据的真实结构。因此，本文以代价函数KL(P||Q)的值在0.05～0.35之间为依据，经过多次实验，对4个混合数据集Credit Approval、Australian Credit Approval、Heart、Adult 的困惑度Perp分别设定为50、50、20、100。

文献[16]指出，kNN分类算法中k 的选择至关重要，为避免k 值选取不当对实验结果准确新造成的干扰，本文选取多个k 值作为参数，每个k 值分别进行5次实验取平均值。

从表2可以看出，k 取不同值时，算法t-SNE、余弦距离、One-Hot 编码、E-t-SNE 在Credit Approval 数据集上的分类准确率分别是0.682 0、0.746 9、0.814 2、0.861 3。通过比较可以发现，E-t-SNE 比其他3 种算法在准确率上分别提高了17.93%、11.44%、4.71%。因此E-t-SNE 算法性能更好。

表2 Credit Approval数据集实验结果

为了更加直观地反应降维以后的数据分布情况，证明E-t-SNE 算法在可视化方面的优势，本文结合低维空间可视化视图作为一种最直观的评价方法。

图2 展示了Credit Approval 数据集在低维空间中的映射视图（类标签只用于染色，不同的颜色表示不同的类）。其中（a）采用独热编码方式计算混合数据集数据点之间的距离降维后得到的视图；（b）采用余弦距离方式计算混合数据集数据点之间的距离降维后得到的视图；图（c）采用E-t-SNE算法处理混合数据集降维后得到的视图。通过观察图2 可以发现，（a）和（b）中两个类的数据点混淆在一起，没有很好的分离，在低维空间中不能明显地发现数据集的类别情况；而（c）则可以直观的发现数据集中存在两个类。

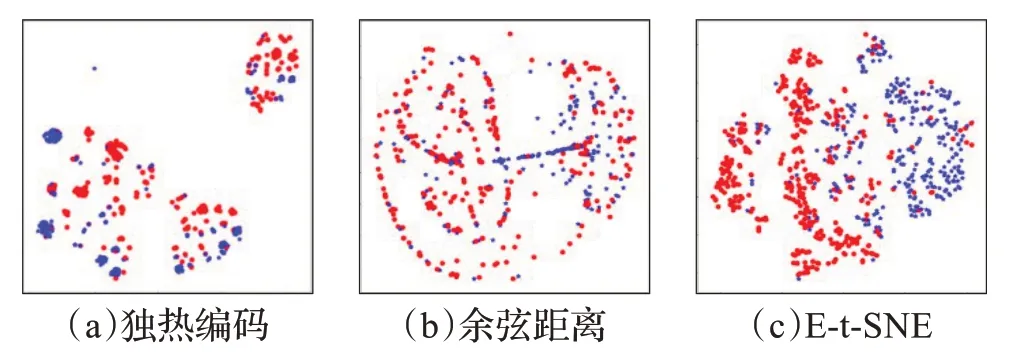
图2 Credit Approval数据集二维空间可视化

从表3 可以看出，k 取不同值时，算法t-SNE、余弦距离、One-Hot编码、E-t-SNE在Australian Credit Approval数据集上的分类准确率分别是0.702 8、0.717 5、0.800 6、0.844 2。通过比较可以发现，E-t-SNE 比其他三种算法在准确率上分别提高了14.14%、12.67%、4.36%。因此E-t-SNE算法性能更好。

表3 Australian Credit Approval数据集实验结果

图3 展示了Australian Credit Approval 数据集在低维空间中的映射视图。其中（a）采用独热编码方式计算混合数据集数据点之间的距离降维后得到的视图；（b）采用余弦距离方式计算混合数据集数据点之间的距离降维后得到的视图；图（c）采用E-t-SNE算法处理混合数据集降维后得到的视图。通过观察图3 可以发现，（a）中两个类的数据点混淆在一起；（b）中数据点分布松散无明显规律；（c）中两个类别区分明显。

图3 Australian Credit Approval数据集二维空间可视化

从表4可以看出，k 取不同值时，算法t-SNE、余弦距离、One-Hot 编码、E-t-SNE 在Heart 数据集上的分类准确率分别是0.678 6、0.689 6、0.756 0、0.795 8。通过比较可以发现，E-t-SNE 比其他两种算法在准确率上分别提高了11.72%、10.62%、7.74%。因此E-t-SNE算法性能更好。

表4 Heart数据集实验结果

图4 展示了Heart 数据集在低维空间中的映射视图。其中（a）采用独热编码方式计算混合数据集数据点之间的距离降维后得到的视图；（b）采用余弦距离方式计算混合数据集数据点之间的距离降维后得到的视图；图（c）采用E-t-SNE 算法处理混合数据集降维后得到的视图。通过观察图4 可以发现，（a）中两个类的数据点分散，很难发现数据集中的隐藏模式。（b）中可以大体发现有两个类别，但类内数据点没有很好地区分；（c）中两个类之间区分明显。

图4 Heart数据集二维空间可视化视图

从表5可以看出，k 取不同值时，算法t-SNE、余弦距离、One-Hot 编码、E-t-SNE 在Adult 数据集上的分类准确率分别是0.737 0、0.740 8、0.753 4、0.791 0。通过比较可以发现，E-t-SNE 比其他两种算法在准确率上分别提高了5.40%、4.93%、3.76%。因此E-t-SNE 算法性能更好。

表5 Adult数据集实验结果

图5 展示了Adult 数据集在低维空间中的映射视图。其中（a）采用独热编码方式计算混合数据集数据点之间的距离降维后得到的视图；（b）采用余弦距离方式计算混合数据集数据点之间的距离降维后得到的视图；图（c）采用E-t-SNE 算法处理混合数据集降维后得到的视图。通过观察图5 可以发现，（a）、（b）两个类的数据点混淆在一起，不能很好地区分类与类之间的关系。（c）中两个类之间虽有混淆重叠，但类间区分明显。

图5 Adult数据集二维空间可视化

图6 汇总了E-t-SNE 算法和对比算法在4 个UCI 数据集上的分类准确度。由图6 可以看出，将选取的4 个混合属性数据集用不同的距离度量方法降维到二维平面后，用kNN 做分类处理，E-t-SNE 算法具有较高的分类准确性。

图6 E-t-SNE算法与其他算法分类准确率对比

以上实验证明了E-t-SNE 算法在对混合数据降维方面有更大的优势。由于引入了信息熵概念，考虑了不同的分类型属性对距离计算时的不同贡献度，使得降维以后的数据更多地保留了数据在高维空间的结构分布，使其在后续的分类算法中获得了更高的准确度。

5 结束语

本文总结了现有的降维可视化算法的原理及特点，指出它们不能有效地处理混合属性数据的缺点。在t-SNE 算法的基础上提出了一种扩展的E-t-SNE 算法，使其能处理混合型数据集。该方法引入信息熵的概念度量混合属性数据点之间的距离，相比于传统的将分类型数据转换成0/1的独热编码方式和将分类型数据转换成向量的余弦距离计算方法，该方法既能处理混合型数据，又不增加数据维度，并且将不同类标签的数据映射到低维空间，有利于更好地理解和发现高维空间数据的结构。通过实验发现，经过E-t-SNE 降维后的混合类型数据集，在后续的数据分析算法中表现出比独热编码方式更高的准确率，证明了E-t-SNE算法的有效性。

E-t-SNE算法能有效地对混合类型数据集进行降维可视化操作。但并没有考虑算法的复杂度和执行时间问题。当数据量太大时，复杂的矩阵运算会占用大量内存和消耗大量的时间。在后续的研究工作中，将考虑算法的复杂度问题，优化求解过程，缩短求解时间。