初三数学复习课中的分层走班教学实践探究

盛秀芬

(浙江嘉兴海盐县滨海中学 浙江嘉兴 314300)

传统的班级上课制度有效率高、规模化的特点，但无法满足不同水平、不同能力的学生的需求。这样的现象在初中数学复习阶段尤为明显。而分层走班教学的出现，正好为解决这一问题提供了方法。

一、用爱心、耐心和细心感化学生，重树他们学习的信心

“学困生”共同的弱点就是自卑感强，自我评价较低。因此，教师首先在思想上应重视他们，用耐心和细心帮助他们总结学习失败的原因，消除其数学学习的畏惧心理。

二、复习中注重基本知识和规律

“学困生”对所学的知识点不能转化成解题能力，不是因为对知识一点也不懂，而是理解得不够全面，不够透彻。因此，教师可以先通过练习了解学生对知识点的掌握情况，对学生学习中出现的错误和缺陷加以纠正并不断训练强化，对个别学生进行跟踪辅导，在复习中补充适当的练习，使每一部分的复习都能达到“知识点测试→信息反馈→矫正强化”这样一个良性循环[1]。

三、复习中精讲细练，由浅入深，循序渐进

“学困生”上课时注意力不太集中，特别是在上课的后半段时间容易走思。因此，教师在课前要精心设计复习内容，合理安排复习进度。课堂复习尽可能在前三十分钟内解决重要内容，授课时言简意赅、突出重点、分散难点、降低起点、减小坡度、避免要求过高。对于难点内容，要适当分解，多台阶、小步走，必要时应适当重复使其易被“学困生”接受，这样有助于他们克服畏惧心理。

四、复习中创造学习氛围，体验成功，激发学习兴趣

“学困生”一般学习兴趣不浓， 学习信心不足。教师在复习中应充分考虑学生的实际，准确选好起点。在教学中创设各种环境，帮助他们克服困难，使他们能够“跳起来摘苹果”，从而获得学习成功的快乐，从而树立他们学习的信心。例如，上课中，教师的语气应是轻松愉悦的；练习应该是基础性较强的，可以选择中考真题中较基础的题目，适当增加一点点的挑战性题目；有难度的题目，分步设疑，减小坡度；同时多多鼓励，多多表扬。

五、复习中瞄准中考，强化双基训练，过好最后一关

一份嘉兴中考数学试卷满分为120分，基础题占总分值的80%左右，即96分左右，这个分值对于“学困生”来说是可望而不可及，但若教师能有计划、有目的、有针对性不断强化双基训练，也是能达成的。针对上述情况，可采取如下措施：

第一，在单元知识复习中，平时多收集中考中常见知识点及相关的基础题，强化训练，熟悉中考。

第二，单元复习后，对中考基础题型进行专题归类，如倒数、相反数、绝对值的类型，分解因式的类型，自变量取值范围的类型，求二次函数的顶点坐标的类型等，使他们对基础题稳操胜券。

第三，每个星期做一份中考综合卷，使他们适应综合性试卷。

通过这样的设计，使他们感悟到中考题对他们来说并不是“洪水猛兽”。

在进行初三总复习“二次根式”的过程中，对于A班的学生，由于其自主学习能力强，有关分式知识的梳理回顾，放在课前的知识任务单中。在课堂教学中，将直接运用题目来回忆知识应用知识，深化知识。

如对于二次根式概念和性质知识这一部分知识点，可以如下设计：

对于B班学生，由于其自主性差，基础薄弱，可由教师带着学生运用题目回顾二次根式的相关知识点，并强化知识点的应用。如在二次根式的概念与性质的回顾中，可进行如下设计：

（让学生理解掌握二次根式被开方数的非负性）

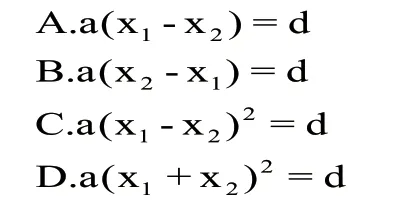
还是以独立思考和组内合作讨论为主要教学形式，同时关注解题速度，注重解题思想的运用，解题方法的多样性。

对于B班学生，基于基础薄弱、积极性较差的劣势，以及课程标准的要求，在这一部分的复习中，重点是回顾一元二次方程的解法，可先出示以下方程：

学生独立完成，教师巡视，并作个别指导，解题后，用投影在全班展示解题优秀的学生，关注解题方法的选择，目的是先通过练习来了解学生对一元二次方程各种解法的掌握情况，并机动性地对学生不熟练的方法进行反复练习，并再次用中考真题中的一元二次方程题让学生求解，成功后表扬学生。同时加大解方程难度，出示系数较为复杂的一元二次方程进行求解，中考中常常会出现系数复杂，但有技巧的解答方式的二次方程，因此方程的求解主要关注方法的选择，对于方程求解非常困难的学生，选择求根公式法较为合适。

函数是中学数学阶段最难的，也是最为重要的知识。对于这部分内容的复习，需要一个循序渐进的过程。以二次函数解析式的求解为例。

A班的学生基础相对扎实，对于函数的认识相对透彻。可以出示以下题目：

1.经过A（4，0），B（-2，0），C（0，3）三点的抛物线表达式_______。

2.已知二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：

?

求解二次函数表达式______________。

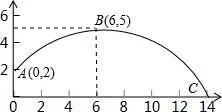
3.在体育测试时，初三的一名高个子男同学推铅球，已知铅球所经过的路线是某个二次函数图像的一部分，如图所示，如果这个男同学的出手处A点的坐标为(0，2)，铅球路线的最高处B点坐标为(6，5)(6，5)，求这个二次函数的解析式____________。

4.建立适当的平面直角坐标系解决实际问题。

如图，一石拱桥呈抛物线状，已知石拱跨度AB为40m，拱高CM为16m，把桥拱看作一个二次函数的图像，建立适当的平面直角坐标系，求二次函数的表达式__________。

对于B班的学生，函数的复习，应该耐心细致，肯花时间，循序渐进。从函数概念开始重新梳理一遍函数的知识，结合相关题目，让学生对函数的认识能相比以往更加深入，多结合直观的图像解决抽象的函数问题，对函数解析式的求解也尽量以图像为起点逐步扩散到文字型求解解析式。

特殊三角形相关知识的掌握对解决基础几何问题至关重要。以等腰三角形中考复习为例。除了要A班学生通过题目回忆等腰三角形相关概念，将着重发展与等腰三角形问题解决有关的分类讨论能力以及计算相关边角能力等。可以让学生解决以下几个题目：

1.等腰三角形的周长为22cm，其中一边的长是8cm，则其余两边长分别为_________。

2.在直角坐标系中，O点为坐标原点，A(2，-4)，动点B在坐标轴上。则满足△OAB为等腰三角形的有B点共有________个。

对于B班学生，要求其掌握最基本的等腰三角形的概念，以及最基本的分类讨论即可。同时，在分类讨论中，注意强调前提是三角形三边关系，三角关系的符合。

六、分层走班的实施原则

（一）走班的时机

分层走班可以是初三复习的开始，也可以进行一轮基础复习后再分班。

（二）走班的发展性

经过第一个学期的一个月或者期中考试，期末考试，学生可自主选择留在哪个教学班级，教师也需要作好充分的引导。

从长时间的实践来看，分层走班对全面提高教学质量，提高学生数学成绩有显著的帮助，虽然在实践过程中遇到了一些困难，做得也有不到位的地方，但相信在未来，分层走班将是教学的一种发展趋势。