高墩大跨连续刚构桥的施工监控

2020-03-18李世平薛旭涛马晓君

建筑施工 2020年11期

李世平薛旭涛刘数马晓君刘进王军

1. 中国建筑第四工程局有限公司广东广州 510665；2. 中建四局第一建筑工程有限公司广东广州 510800

高墩大跨连续刚构桥跨越能力强，整桥的受力合理，整体性好、刚度大，因此被广泛应用于贵州等地质条件复杂的山区[1]。该类型桥梁的缺点主要在于其墩梁固结的连接形式，上部结构和下部结构之间通过刚性连接，不设置支座，导致桥梁本身对温度变化、混凝土收缩徐变等因素产生的次内力十分敏感。因此，需要在施工过程中对桥梁的结构稳定性进行监测[2]，以保证桥梁施工质量和安全，确保在使用过程中不发生事故。

本次研究依托贵州省松桃至玉屏快速路项目中的某大桥，为高墩大跨连续刚构桥，全桥墩柱高度最低为79 m，最高达到了112 m。墩身为钢筋混凝土结构，设计为直立式矩形空心墩，壁厚0.8 m，每隔20 m设置一道横隔板。该桥的跨度大，主跨的跨径达到了125 m，主跨使用挂篮悬臂浇筑工艺进行施工。

由于该大桥跨越山谷，为了满足地形要求，墩柱设计较高，同时地势环境恶劣，施工多为高空作业，极大地增加了作业风险，给现场管理造成了很大困难。为保证桥梁的施工质量和施工安全，对桥梁施工进行全过程监控，主要内容有桥梁墩柱标高和梁段的应力情况。技术人员使用有限元软件对桥梁的受力情况进行模拟，预先计算出施工中各阶段桥梁的内力和位移，将施工中的实测值与预计值进行比较，在发现较大的误差时可迅速调整施工参数，使桥梁在施工各阶段的内力和变形在设计和规范的允许范围内，保证桥梁的内力状态和结构线形满足设计要求[3-8]。

1 连续刚构桥的受力分析

对松桃至玉屏快速路项目中的某大桥建立三维模型，根据施工图设置节点划分梁段，便于后期比较同一梁段的理论计算值与实际监测值的区别，计算两者误差，达到保证桥梁受力安全的目的。该大桥上部结构为现浇箱梁，设计采用C55混凝土，弹性模量取3.45×104MPa，泊松比取0.187，容重取24.7 kN/m3。

由于高墩大跨连续刚构桥进行受力分析时是作为典型的弯压构件考虑，所以结构材料需考虑非线性影响[5]。设混凝土轴心抗压强度为fc，参照德国学者Rusch的混凝土轴心受压应力-应变（σ-ε）曲线模型[6]，该模型的本构关系如式（1）所示：

桥梁墩柱设计的材料为C40混凝土，C40混凝土的抗压强度标准值为26.8 MPa，因此本项目所用混凝土在计算时的名义屈服应力取21.44 MPa。

根据本桥设计图，使用Midas Civil软件建立有限元分析模型，如图1所示。

图1 大桥有限元模型

2 桥梁竖向线形误差调整方法

受高空作业限制，高墩大跨连续刚构桥在施工过程中的竖向线形监测和调整非常困难，由于受到施工图设计过程中绘图参数精度误差、结构分析理论计算误差、现场测量误差等多种因素的影响，导致现场测量结果和设计图纸计算理论结果出现误差。

在本工程桥梁上部结构的施工过程中，竖向线形误差预测的理论方法主要是灰色系统预测理论[7]，通过预测预应力张拉后桥梁的预拱度，调整模板预拱度设置值，使施工过程中桥面的标高误差能够尽量缩小，达到理想的计算结果。

2.1 灰色系统预测方法原理

由于桥梁施工过程中，存在已知和未知2种不同类型的数据信息，对于重要未知信息需要提前预测，降低出现误差的可能性以及误差的数值。因此，在桥梁工程施工中需要依靠灰色系统理论建立误差微分方程模型，针对桥梁上部结构施工，挂篮就位后需根据误差的预测结果对下一阶段的模板标高进行调整，以达到控制误差的目的。

2.2 灰色系统误差微分方程模型建立

结合灰色系统误差分析方法，在使用挂篮悬臂浇筑施工时，挂篮就位后需在下一梁段施工前调整挂篮底模标高，预测其在梁段预应力张拉后的预拱度，在计算得到施工梁段张拉后的理论标高，同时现场测量得到实际标高后，通过之前采集数据分析标高的误差，计算下一阶段的预拱度调整误差值。微分方程模型建立方法如下：

在第i＋1号梁段施工前，通过计算得到已施工完梁段i在预应力钢绞线张拉后的理论标高值，同时现场测量得到预应力钢绞线张拉后的实测标高值，对两者建立误差序列，建立误差微分方程，计算方式如式（2）所示[8]：

对公式（2）中的各项参数分别进行介绍：x为施工完梁段在预应力张拉后的理论标高值序列；y为施工完梁段在预应力张拉后的实际标高值序列；x(n)为第n号梁段在预应力张拉后的理论标高值；y(n)为第n号梁段在预应力张拉后的实际标高值。根据每一个梁段在预应力张拉后的理论标高值和实际标高值之差，建立误差序列，对于第k号梁段，其误差如式（3）所示：

在式（3）中，a＝max[|x(k)－y(k)|]，其中k＝1,2,…,n。

在桥梁施工过程中，影响施工质量的因素有很多种，对于某一种变量，使用δ(k)为数据，组成新序列X(0)，进而经过计算，由X(0)得出X(1)。以此为基础，优化误差分析的精确度如式（4）所示：

式（4）中X(1)(i)按式（5）计算：

X(1)(k)和X(1)(k＋1)的平均值，组成式（6）所示数列Z(1)：

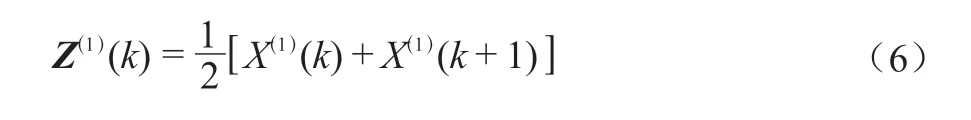
对于X(0)、X(1)，设有系数b、v，则各数据之间存在的数学关系如式（7）所示：

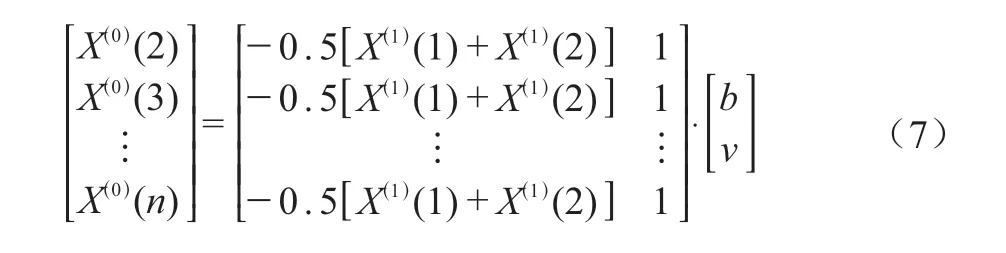
由式（7）可知，灰色系统误差微分方程为〔式（8）〕：

对于本工程在实际施工过程中灰色系统控制理论的应用，现选用建立的有限元模型中8号桥墩5#块为例，展示在实际施工过程中，灰色系统控制的应用。此处桥梁标高均以毫米作为单位，便于误差计算。

8号桥墩5#块梁段在预应力张拉后的理论标高值为：[83 762 83 758 83 743 83 766 83 752]。

8号桥墩5#块梁段在预应力张拉后的实际标高值为：[83 764 83 760 83 744 83 769 83 754]。

误差序列为：[－2－2－1－3－2]。

2.3 线形坐标数据的处理与分析

2.3.1 观测点的设置

在施工过程中，通过灰色系统误差微分方程模型完成施工误差修正，使结构的实际状态接近理想状态。在本工程施工过程中，进行现场标高测量，得到标高控制结果。

2.3.2 观测结果和计算值分析

节点编号采用有限元计算时建立模型所设置的节点，以便于统一节点编号。通过灰色控制理论的计算，针对性调整对本工程大桥每一梁段的预拱度值，将经过计算后桥梁的标高和实际测量的标高进行对比，桥墩施工标高控制结果如表1所示。

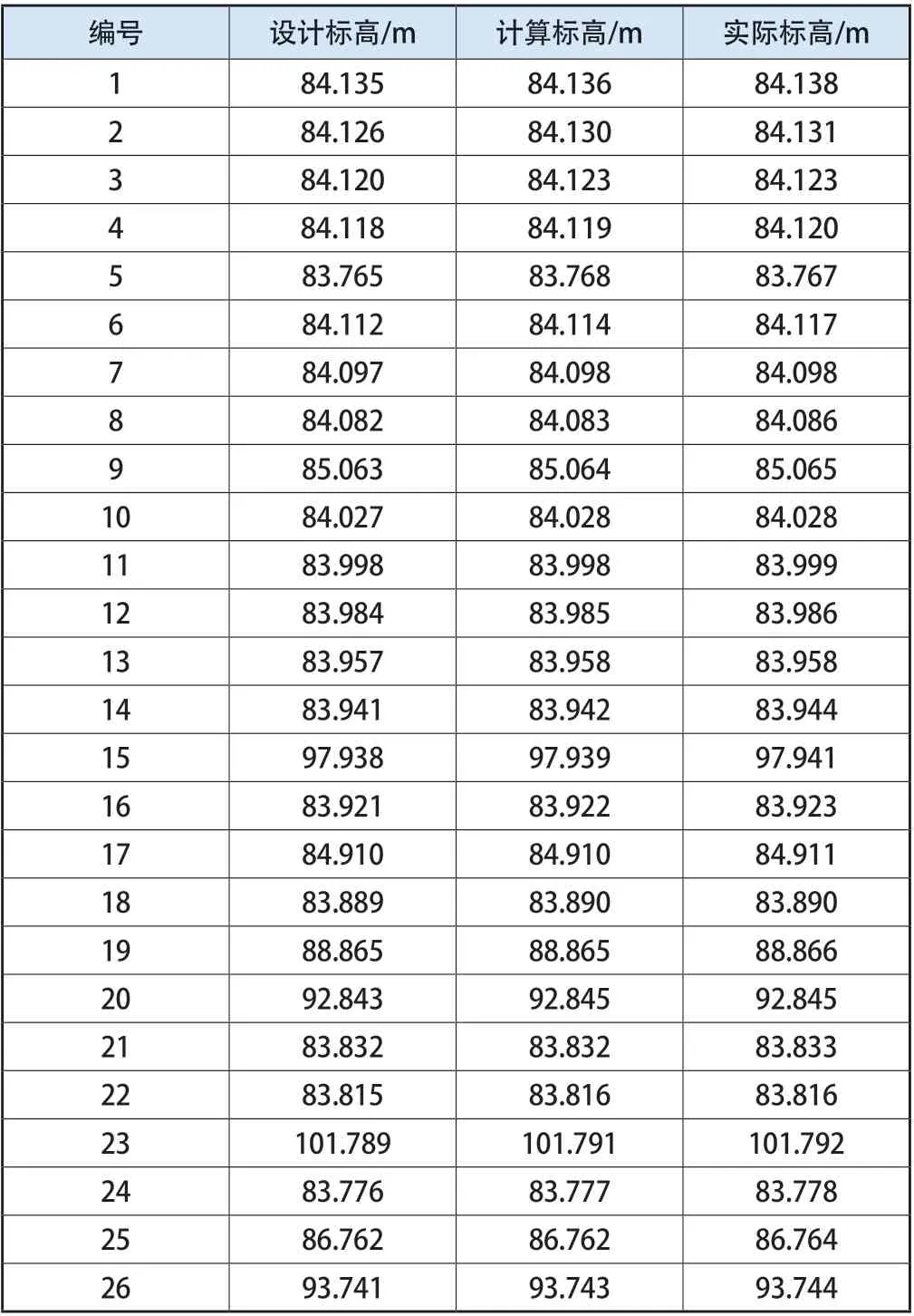
表1 本工程大桥桥墩标高控制结果

对表1的数据进行分析，可看出桥梁的实际标高和计算标高满足设计要求，且实际监测数据和设计标高、计算标高接近。由此可见：通过灰色系统微分方程模型计算后，调整桥梁预拱度，对桥梁竖向线形误差的控制效果明显。

3 大桥应力监测

3.1 箱梁控制截面应力测点布置

箱梁应力测点选取在桥梁结构受力关键截面，共在9个截面布置传感器进行监测，箱梁各根部截面应布置12个测点，传感器的布置方向均为顺桥向布置。在试验前应预先进行试验室内模拟测试，观测所用仪器的工作情况，确保试验所使用的传感器均能正常工作，记录数据真实可靠。

3.2 应力测试结果分析

使用Midas Civil软件对模型进行应力计算，统计出对应界面的应力理论计算值，再与监测的实测值进行对比分析。应力监控作为确保桥梁施工中结构安全的重要手段，在大跨径连续梁的施工中得到广泛应用。使用传感器对桥梁的应力进行监测，同时与有限元模型计算出的理论值进行对比，可以准确判断出桥梁是否处在安全的状态下进行施工。

计算值、监测值两者之间的对比，能够精准地将桥梁应变控制在合理范围内，最大限度地保证施工安全。

通过对桥梁的应力进行监测，并分析数据，监测结果表明桥梁混凝土应力和理论值之间吻合性较好，结构安全系数高。