考虑煤层倾角和钻孔倾角的钻屑量理论研究
2020-03-18石占山孙维吉
周 洋,梁 冰,石占山,孙维吉,刘 学
(1.辽宁工程技术大学 矿业学院,辽宁 阜新 123000;2.辽宁工程技术大学 力学与工程学院,辽宁 阜新123000;3.煤炭科学技术研究院有限公司 安全分院,北京 100013)
煤与瓦斯突出是煤矿中发生的极为复杂的煤与瓦斯涌出现象,是严重威胁煤矿安全生产的主要灾害之一[1-3]。国内外广大科技工作者虽已对煤与瓦斯突出问题进行了较深入的认识和研究,但深部开采情况下地质条件复杂、受高地应力及其他各种因素影响,煤与瓦斯突出灾害问题还未根本解决。由于钻屑量是煤体应力的综合反映,是煤矿煤与瓦斯突出预测和预防的主要指标之一,因此,研究影响钻屑量及相关规律的因素对煤与瓦斯突出的预测和预防具有重要意义[4-7]。
对于钻屑法的研究,国内外学者很早便开展了大量的理论和实验研究工作。勃罗纳[8]将钻屑排放分为两部分,其中一部分与圆柱形煤体的钻孔直径相同,另一部分是钻孔内壁的位移产生量;王佑安[9]通过Mohr-Coulomb准则分析了利用钻屑量如何反映煤体应力的问题;潘一山[10]通过考虑膨胀因子等因素,得到钻屑量与煤体应力间的关系;王振等[11]提出了应力梯度下钻屑量的增量变化指数;曲效成等[12]确定了钻屑量和钻孔应力之间的联系;董杰等[13]分析了煤岩物理和力学性质,压力和测量误差对钻屑量的影响;陈峰等[14]研究了最大钻屑量对冲击地压的影响;王志明等[15]指出围岩的应力状态可以通过钻屑法确定。
我国的大部分煤层都有倾角,随着开采深度的增加,水平地应力的作用也越大,同时在打钻时钻孔倾角也会对水平地应力的计算产生一定影响。因此在考虑煤层倾角与钻孔倾角因素下,通过对有效地应力的计算修正,从而建立新理论公式并对钻屑量与煤层倾角和钻孔倾角之间的关系进行分析,根据平煤有限公司八矿的钻屑量实测值,对钻屑量的新理论公式进行了对比验证,为准确预测地应力提供参考。
1 考虑倾角的钻屑量公式研究
从理论分析角度,深部开采条件下,钻孔倾角与煤层倾角对水平地应力的作用不能忽略,引入钻孔倾角与煤层倾角推导得到新钻屑量公式。
1.1 模型的建立
采用Mohr-Coulomb准则进行分析,建立了钻孔围岩应力分布力学模型,如图1所示。其中,σv为垂直地应力;σh为最小水平地应力;r为钻头半径;R0为破碎圈半径;R为非弹性变形区半径。
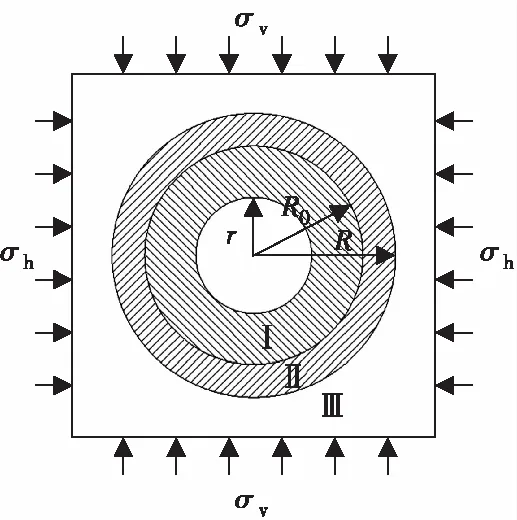
Ⅰ—破碎区;Ⅱ—塑性软化区;Ⅲ—弹性区。
1.2 新钻屑量公式推导
钻孔钻屑量主要分为静态部分和动态部分钻屑量。静态钻屑量即钻孔实芯部分G1;动态钻屑量由钻孔弹性变形区部分G2,破碎区与弹性区交界处部分G3,煤体扩容部分G4组成。总钻屑量为:
G=G1+G2+G3+G4
(1)
钻孔煤体实芯部分G1表示为:
G1=πr2ρ0
(2)
式中:r为钻头半径,mm;ρ0为原始煤体密度,g/cm3。
钻孔弹性变形部分G2表示为:
(3)
式中:μ为煤体泊松比;E为煤体弹性模量,MPa;σe为有效应力,MPa。
采用易俊等[16]试验推导的有效应力σe计算公式:
(4)
式中:σv[sin2(90°-α)+Kcos2(90°-α)]-1为引用汪大海等[17]推导的正应力计算公式;σH为最大水平地应力,MPa;α为钻孔倾角,(°);K为煤层侧压系数;p1为钻孔非弹性区瓦斯压力,MPa;p2为钻孔形成后周围的瓦斯压力,取0.1 MPa。
煤层的水平应力主要由上覆岩层压力、构造运动的作用引起,而煤层倾角和钻孔倾角的存在也影响了水平地应力与垂直地应力的计算,笔者引用楼一珊[18]推导的煤层侧压系数计算公式:
K=KαKβ
(5)
式中:Kα为钻孔倾角影响系数,Kα=(α+β)/(α-β);Kβ为煤层倾角影响系数,Kβ=β/(α-β);β为煤层倾角,(°)。
考虑煤层倾角与钻孔倾角的水平地应力计算模型为:
(6)
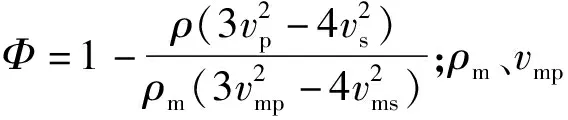
G3为破碎区与弹性区交界处因弹性卸载产生的附加钻屑量:
(7)
(8)
式中:K1为破碎区煤体的三轴残余强度系数;R0为破碎圈半径,mm;σ0为煤体残余强度,MPa。
G4为钻孔形成后,煤体扩容钻屑量。煤体应变软化本构方程为:
(9)
式中:m为煤体塑性软化系数;σc为单轴抗压强度,MPa;εc为单轴抗压强度相应的应变。
依据 Mohr-Coulomb 准则,建立弹塑性平衡方程为:
(10)
式中:σθ为径向应力,MPa;σr为切向应力,MPa。
屈服条件为:
σθ=qσr+σc
(11)
边界条件:当r=R0时,σr=0;当r=R时,得出非弹性变形区半径R的解析式为:
(12)
当m=0时,式(12)即为理想Kastner公式。在不考虑扩容情况时,钻孔非弹性部分与弹性部分交界处的径向位移uR为:
Kcos2(90°-α))-1-σc]}
(13)
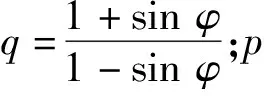
孔内壁径向位移由体积不变条件得:
(14)
考虑煤体非弹性变形扩容时的孔内壁径向位移ur为:
(15)

综上可得,扩容单位孔深钻屑量G4推导为:

(16)
由以上推导可得新钻屑量G为:
(17)
式(17)即为考虑钻孔倾角和煤层倾角情况下新钻屑量理论公式。
1.3 新钻屑量公式影响因素分析
从式(17)可以看出,煤层倾角和钻孔倾角对钻屑量有一定的影响。以典型的高瓦斯突出矿井——平煤股份有限公司八矿为例,取屑钻孔直径为 94 mm,通过对新钻屑量公式进行分析,并将表1中的物理力学参数代入到式(17)中,得出在考虑钻孔倾角与煤层倾角影响下的新钻屑量变化规律。
我国煤矿井下条件较为复杂,煤层的赋存条件不同[21],大多数煤矿煤层不同程度地存在着煤层倾角,并且随着开采深度的加大,由于重力势能作用,对地应力的影响越大,而打钻时钻孔倾角也影响着钻孔受到的垂直应力和水平应力的大小,在两者共同作用下钻屑量的大小必然也会受到影响。由式(4)~(6)可知,在考虑煤层倾角与钻孔倾角因素下与钻屑量的关系如图2~4所示。

图2 钻屑量与煤层倾角和钻孔倾角间的关系
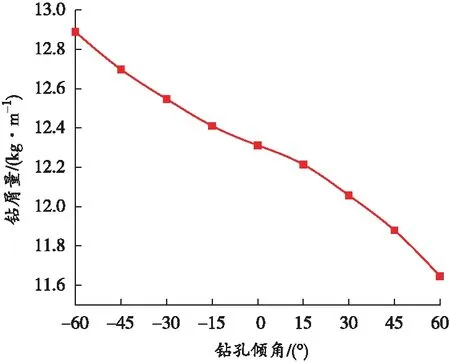
图3 煤层倾角0°时钻屑量与钻孔倾角变化关系

图4 钻屑量减小比率随钻孔倾角的变化关系
从图2~4可知,钻屑量与煤层倾角和钻孔倾角均呈幂指数递减关系,且递减幅度先大再逐渐减小后再次逐渐增大。煤层倾角与钻孔倾角对钻屑量的计算有较大影响,当煤层倾角较小时影响较小,煤层倾角较大时影响较大;当钻孔倾角较小时影响较小,钻孔倾角较大时影响较大。主要原因是大多数煤层是各向异性体或横观各向同性体,其各方向上的弹性参数是不相同的,当煤层具有一定倾角时,这种差别更为明显。而钻孔具有一定倾角时,所受水平地应力与垂直地应力均会不同程度的变化,变化幅度随倾角增大而增大。因此,对于大倾角煤层、深部开采高地应力、高瓦斯压力矿井,考虑煤层倾角与钻孔倾角因素计算钻屑量预测煤与瓦斯突出是十分有必要的。
2 现场对比验证
在平煤股份有限公司八矿己15-21030风巷进行钻屑量实测研究,对比验证新钻屑量理论公式准确性。平煤股份有限公司八矿己15-21030风巷现场基本情况如下:地面标高+75~+90 m,己15煤层区段标高-728~-840 m,埋深803~930 m;工作面按综采工作面布置,采高3.5 m,平均采长205 m,可采走向长1 568 m,储量147万t;煤层厚度一般在3.0~4.4 m内,平均厚度为3.5 m,煤层倾角一般为5°~15°;该工作面正常涌水量为2~3 m3/h,最大涌水量为 5 m3/h,属突出危险工作面。己15-21030风巷钻孔钻屑量G(采用称重法)测试:钻孔采用ZYWL-4000SY煤矿用双履带式全液压钻机钻进,搭配直径94 mm螺旋钻杆,煤层实际倾角为14°,钻孔开孔高度1.2 m,每个钻孔实际钻进15 m,取前10 m钻屑量进行测试,现场在同一区域排除其他影响因素的情况下共计测试5个钻孔,钻孔间距2 m。钻屑量现场实测值如表 2 所示。
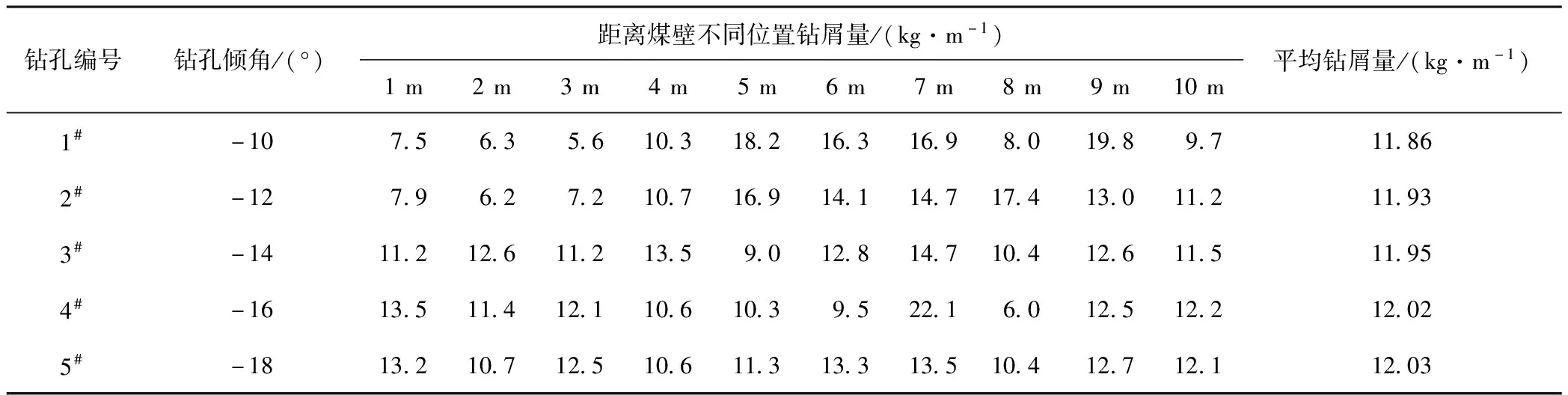
表2 钻屑量实测值
将表1中平煤八矿的煤体力学参数代入到新钻屑量公式中,计算出钻屑量理论值,并将其与现场实测值进行误差对比分析,分析结果如表3所示。

表3 钻屑量理论值与实测值误差分析
从表3中可知,原钻屑量理论值误差随着倾角的变小逐渐减小,而在考虑了煤层倾角与钻孔倾角影响下的新钻屑量理论值误差波动较小,为3.9%。
3 结论
1)在煤层倾角一定时,钻屑量随钻孔倾角增大呈幂指数递减关系,减小的比率呈“V”形变化趋势;在钻孔倾角一定时,钻屑量随煤层倾角增大呈幂指数递减关系,减小的比率也呈“V”形变化趋势。
2)工程实例中考虑煤层倾角与钻孔倾角影响因素,计算得到的钻屑量与现场实测值平均误差为3.9%,比原钻屑量理论值平均误差(5.5%)减小1.6%。说明在考虑煤层倾角与钻孔倾角影响因素下建立的新钻屑量公式是有效合理的,更适用于矿山深部开采与现场实际情况,能为预测与防治煤与瓦斯突出提供参考。
