随机状态下基于期望经验回放的Q学习算法

张 峰，钱 辉，董春茹，花 强

河北省机器学习与计算智能重点实验室，河北大学数学与信息科学学院，河北保定071002

Q学习算法[1]是一种用来解决马尔可夫决策问题[2]的流行算法．与动态规划的值迭代和策略迭代算法相比，Q学习算法能应用于对模型未知的环境中，通过对环境采样，基于Bellman最优方程，采用Bootstrap方式来迭代更新状态-动作的Q值与最优策略．Q学习算法的更新公式[2]为

Qt(s,a))

(1)

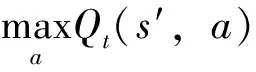
Q学习算法的收敛速度与经验数量指数相关[3]．为进一步提高Q学习算法的收敛速度，研究人员提出了很多Q学习更新算法. 如Q(λ)算法[4]、后向Q学习算法[5]等．但是这些改进算法通常会将实时采样数据更新后就丢弃，造成两个问题：① 对于那些不容易被采样的状态，仅使用1次会造成数据利用效率降低；② Bellman方程中每个Q值的更新依赖于后续状态中的Q值，使用逆序访问序列的收敛速度更快，而标准形式的Q学习算法中Q值更新是按正序访问序列方式更新的，收敛速度较慢．针对这些问题，LIN[6]提出经验回放算法．随后MINH等[7]将其扩展到深度学习领域，提出深度Q网络(deep Q-network, DQN)算法，通过构造经验池保存历史经验，再采用经验回放的方法，在必要时再次使用历史经验．该算法打破了状态转移之间的强关联性，不仅保证了监督学习中数据独立同分布的假设，还加快了算法收敛速度，提高了数据利用率．

目前关于深度强化学习的研究中，针对经验回放主要采取两种方式：① 均匀回放，即将采样序列〈s,a,r,s′〉保存到经验池中，等概率选择经验池中的经验，并应用式(1)更新Q值；② 优先回放，即优先回放TD-error值较大的经验，以提高收敛速度，优先回放的经验结构与均匀回放的经验结构一致．但是，这些方法只适用于状态转移确定的情况，当系统的状态转移不确定时，两种方法都不能保证回放经验的状态转移分布与实际状态转移分布一致．另外，在DQN算法中，由于Q学习算法总是贪心地选择后续状态动作对中的最大Q值，因此可能会出现Q值过估计现象[8]．为此，本研究提出一种新的采样序列存储结构，改进了迭代计算公式，并提出基于状态-动作对的期望Q值经验回放方法．该方法在保证算法复杂度较低的情况下，实现对于环境状态转移的无偏估计，并在一定程度上减少了Q学习算法的过估计问题．

1 经验回放

经验回放通过agent对环境的多次采样来提高强化学习算法的收敛速度并解决更加复杂的问题[7]．由于经验可存储在agent的经验池中，减少了等待环境反馈的时间，减小了agent与环境交互的代价．相比策略梯度类算法[9]，基于经验回放的值评估算法能将采样效率提高约10倍[10]．与基于模型的算法不同的是，经验回放机制的所有状态转移序列都来自真实环境，避免了因模型拟合准确度问题而造成的偏差．

但是，在不确定性的系统中，即使agent执行相同的动作，agent观察到的环境也可能会转移到不同的状态．与不同后续状态的转移概率不同，仅经验回放选择的状态转移分布与实际环境一致时，才能保证最终的Q值是准确值．

DQN算法通过经验回放减少了状态转移序列的相关性，并通过批量选择经验进行小批量更新，并多次回放经验，提高了经验利用率[11]．为进一步提升算法速度，优先经验回放[12]通过给每个状态转移序列加权，将权重设为TD-error的幂函数，再以大概率选择回放TD-error值大的序列，从而加快收敛速度．但是，此方法会令状态转移分布与实际环境不一致，必须对经验的更新值进行修正，让每个更新值都乘以重要性采样权重[12]．当每个经验都需按权重回放时，又会极大地增加算法的复杂度．因此，为减少复杂度，在优先经验回放中新增了sum-tree结构，用来保存经验的回放优先级，以实现快速获取经验．

由以上分析可见，均匀回放不需进行重要性采样加权，算法简单，但学习效率较慢．在经验池足够大的情况下，可认为经验的状态转移概率与环境一致，因此采用均匀经验回放可近似保证状态转移分布与实际状态转移分布的一致性．基于优先回放的Q学习算法学习效率有所提高，但是相对复杂，对于随机性较大的动态系统，优先经验回放打破了原有的经验分布，用于处理不确定环境时，效果可能更差．因此，本研究通过改进现有经验存储方式，设计基于期望经验回放的Q学习算法．该方法在保证算法复杂度较低的情况下，可实现对于不确定环境状态转移的无偏估计，并保证用于计算Q值的状态转移概率与实际环境的状态转移概率一致．

2 期望经验回放

为解决优先经验回放所带来的问题，本研究重点关注优先回放算法造成的有偏回放以及复杂的数据结构问题．为使经验回放的状态转移分布与真实的状态转移分布一致，考虑以采样获得的状态转移频率μn/n作为环境状态转移分布P的估计值．

由伯努利大数定律

(2)

可知，估计值μn/n为后续状态分布概率的无偏估计．其中，ε为任意实数．因此可将此估计值带入迭代公式，获得动作价值更好的估计．

采用这种经验存储结构，可实现在特定状态下执行同一动作时，无需更新整个经验，只更新经验池中后续状态的访问次数和即时回报期望值．每个经验样本相当于一个完整的状态转移子树，当采样次数足够大时，可直接以等概率方式回放经验，且多次回放经验仍是无偏估计．更新公式修订为

Qt(s,a)]

(3)

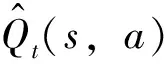
(4)

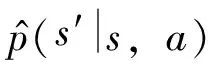
图1 期望经验回放算法

Fig.1 Expected memory replay-based
Q-learning algorithm

与原均匀经验回放与优先经验回放算法相比， 本研究算法具有以下优点：

2) 经验池中的每个样本包含多个序列，增加了经验池的使用效率．

3) 每次经验回放相当于回放多个转移序列的期望，经验利用率比原均匀回放算法更高，而经验池的结构比优先经验回放更简单且易于实现．

4) 由于使用了后续状态价值的期望，由式(5)可知，每次更新的TD-error 值都更稳定，这在一定程度上减小了Q学习算法对动作价值的过估计问题[13]．

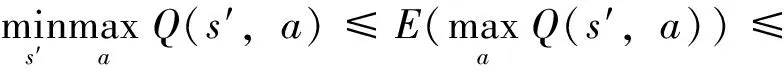
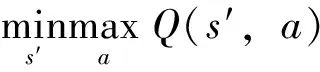
(5)

在采用TD评估方式更新Q值的方法中，评估值的方差可分为立即回报方差、状态转移方差和后续估计值方差之和[14]．采用期望经验回放，将使得状态转移方差变为0，加快了算法收敛速度．

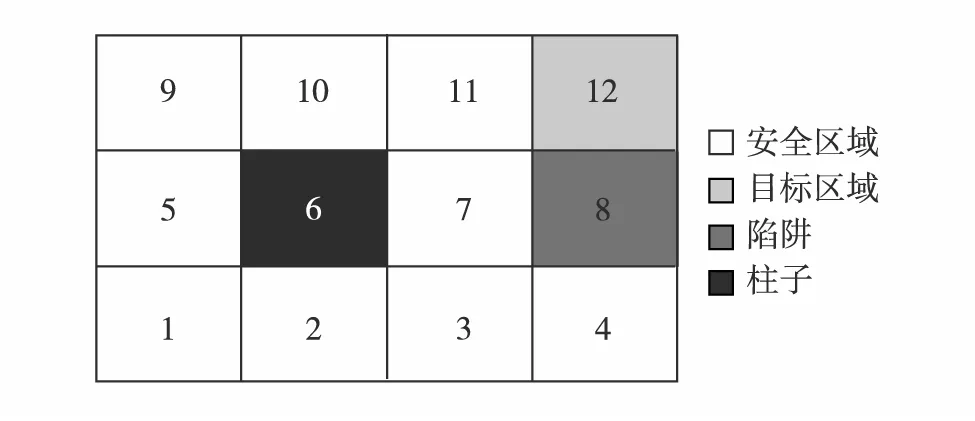
图2 机器人随机行走问题Fig.2 Robot random walk

3 实 验

3.1 实验设置

设计一个简单的带有障碍的机器人行走环境(如图 2)，并在此环境下分别测试原始Q学习算法、均匀回放算法、优先回放算法及本研究算法收敛到最优策略的速度．假设有一个机器人处在一个3行4列的网格中，其任务是到达位置12，在位置8处有一个陷阱，一旦机器人进入则会损坏；位置6处有一根柱子，机器人若碰到柱子则会停在原地．网格周围都是高墙，机器人碰到墙，就会停留在原地．

机器人可站在图2的空白区域，可向上下左右走，但限于控制精度，仅有0.8的概率走到预定位置．例如，若机器人在位置 3往上走，则有 0.8 的概率走到位置 7，0.1 的概率走到位置 2或位置4；若机器人从位置 1往上走，则有 0.8 的概率走到位置 5，0.1 的概率走到位置 2和位置1．

任务目标是在任意空白位置，求机器人行走到达位置 12的最佳轨迹．为使机器人避开陷阱，到达位置 12，可将到达位置 12 的回报设为 1 000，到达其他位置的回报设为 -1，折扣设为 1．同时，为提供一个比较的基准，基于此设置，先利用值迭代算法求得该问题真实的最优策略如图 3．

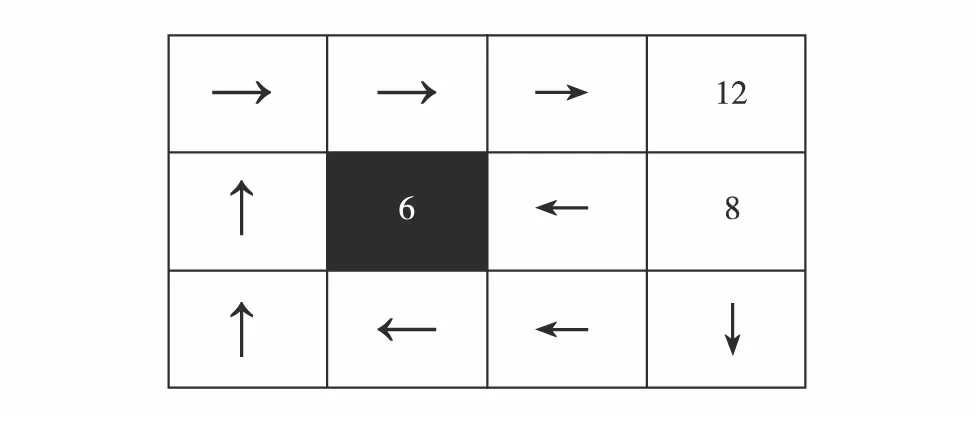
图3 机器人行走环境的最优策略Fig.3 The optimal policy in the robot walk environment

根据Bellman最优方程，得到最优策略下对应于各状态动作价值如表1．

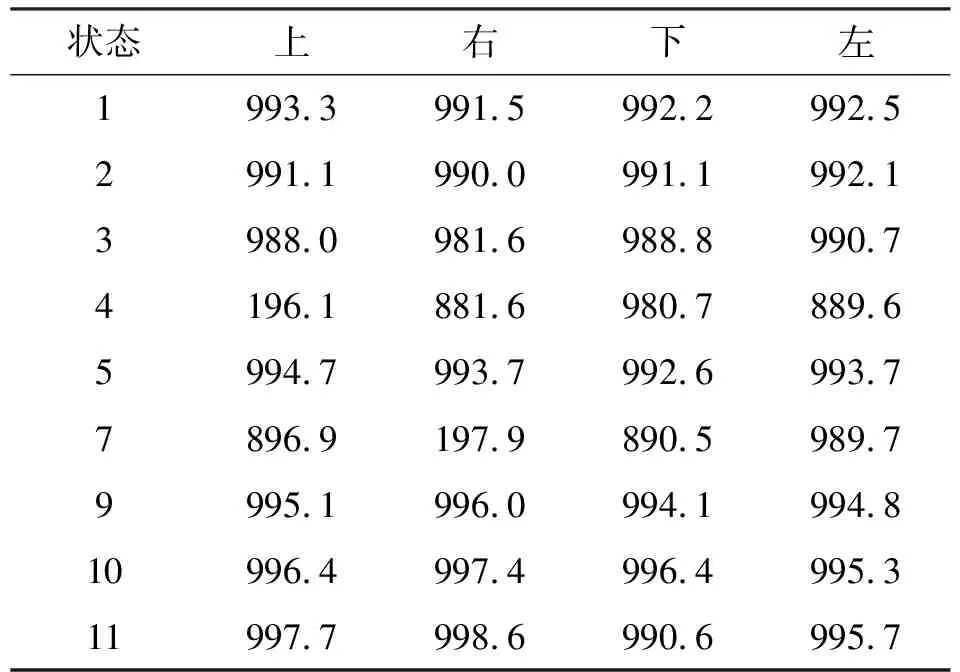
表1 最优策略下动作价值

分别用经典Q学习算法、带均匀回放经验、带优先经验回放和动作期望经验回放的Q学习算法对机器人行走环境求解最优策略，每种算法测试1 000 次，通过比较算法收敛到最优策略所需的采样数量，以及算法的收敛速度．

3.2 实验结果

由于不同算法适合的超参数不同，本研究对每个算法分别进行多次实验，取其平均最优结果，再统计各算法收敛到最优策略时所需采样次数的均值与标准差．收敛测试结果表明，经典Q学习算法、随机经验回放算法、优先经验回放算法和期望经验回放算法在各自最优参数下，收敛到最优策略所需的平均采样次数及其标准差分别为(6 734±533)、(2 200±255)、(2 678±847)和(1 260±386) 次．可见，期望经验回放算法收敛到最优策略所需的平均采样次数仅为原始Q学习算法的1/5、方差较小且收敛速度比均匀回放算法和优先回放算法均提高了约50%．优先回放算法使回放的状态转移分布与实际环境不一致，因此方差最大．(详细测试结果请扫描论文页末右下角二维码查看．)为保证实验的可复现性，提供期望经验回放算法取得最好结果的参数为：学习率α=0.005， 开始回放步数startStep=2 000，回放周期period=4，回放数量replaySize 从8递增到 32，即在每回放100次后回放数量加4．实验表明，采用动作期望经验回放的方式，明显提高了算法收敛到最优策略的速度，对于动态环境更有优势．

3.3 算法的进一步分析

在算法迭代过程中，所求策略总是会先收敛到一个次优的策略．图4给出了一个收敛过程中最先出现1个次优策略的例子．

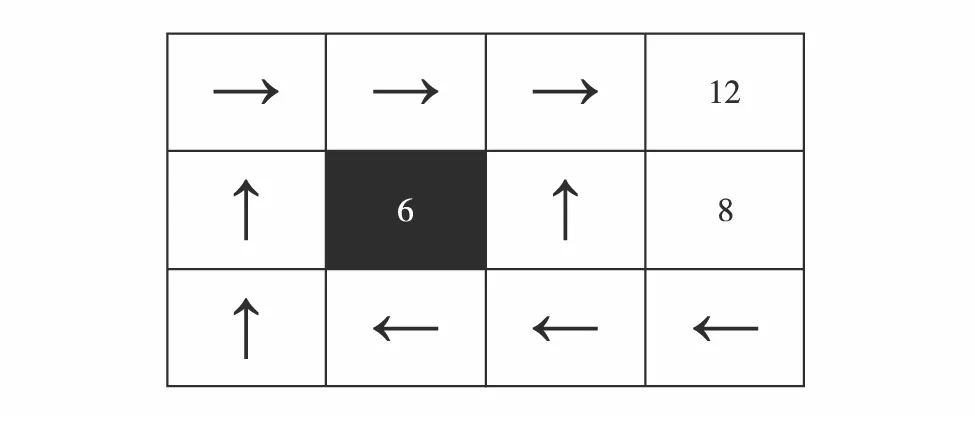
图4 收敛过程中的次优策略Fig.4 An example of suboptimal policy in convergence process

由图4可见，此策略是到达目标的最短路径策略，直观上是最优策略．但在状态 4 和 7 处，最短路径策略风险较高，这是因为算法迭代过程中分别对状态4向左和状态7向上的动作产生了过估计．由式(4)可知，本研究算法对状态4和7的动作价值估计更稳定，且在迭代过程中保留了动作价值的序关系，保证了算法能够快速收敛到最优策略．

表 2和表3分别给出了基于均匀回放的Q学习算法和基于期望回放算法收敛到最优策略后的平均动作价值与真实动作价值的误差统计．

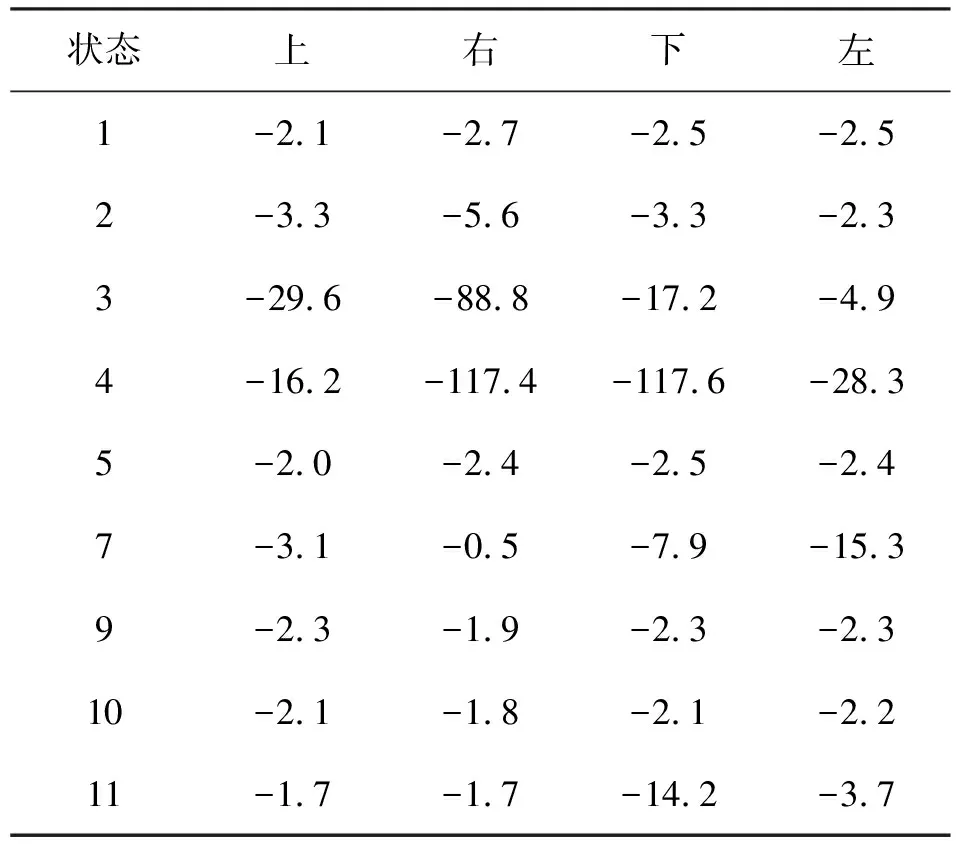
表2 基于均匀回放的算法收敛后动作价值的误差

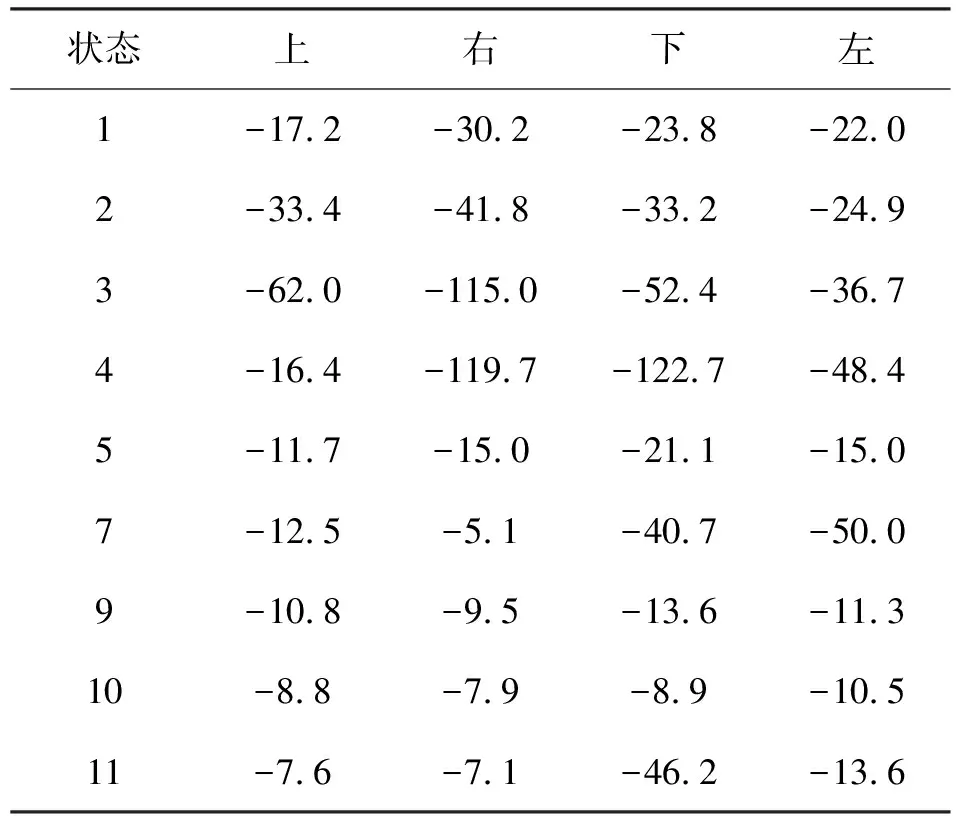
表3 基于期望回放算法收敛后动作价值的误差

由表2和表3可见，当算法收敛到最优策略时，对于所有状态，动作期望回放算法最终的动作价值比均匀回放算法的动作价值要低，但都收敛到了最优策略，说明动作期望算法有效解决了Q学习算法的动作价值过估计问题．

结 语

提出一种基于树的经验存储结构，并将随机环境的后续状态转移频次保留到经验存储的结构中来估计实际环境的转移分布，设计了具体算法．实验结果表明，该算法可行且有效．相比于原有经验回放方式，本研究提出的基于期望的经验回放模型存储更加高效，数据利用率更高．由于算法采用了更稳定的迭代计算公式，有效降低了Q学习算法的过估计问题，对于动态系统的策略收敛速度更快．下一步，我们将深入研究包括如何用近似模型对状态转移概率进行拟合，以及如何设计有效的算法以使算法收敛更加稳定．另外，拟采用参考经验回放的连续思想[15]对算法进行扩展.