需求可拆分下城轨关联的公交接驳线网优化

邓连波，何 渊，曾俊豪，周文梁

中南大学交通运输工程学院，湖南长沙 410075

在城市公共交通系统中，城市轨道交通与常规公交之间的有效衔接，对于充分发挥公共交通的网络化优势具有重要意义．为此，在进行公交线网设计时，需要充分考虑轨道交通线路的走向和站点分布，由此形成公交接驳线网问题(feeder-bus network-design problem, FBNDP)，即针对存在的一个轨道交通系统，设计对应的公交接驳线路网络，使之形成一个整体的接驳换乘系统．FBNDP通过接驳车站、线路经由及开行频率[1]确定城市公交接驳线路方案．

KUAH等[1]提出，由于FBNDP包含旅行商问题且目标函数具有非线性，是一个典型的多项式复杂程度的非确定性问题，即NP难(non-deterministic polynomial hard, NP-hard)问题，适于采用启发式算法求解．BYRNE等[2]对KUAH等[1]建立的公交站点和轨道车站间“多对一”的规划模型进行求解，并提出FBNDP．LENSTRA等[3]验证了遗传算法对于求解类似于FBNDP这种包含多个变量和多个约束的NP难问题，具有较高的适应度和匹配性．KUAN等[4]也通过遗传算法得到FBNDP较好的解形式．邓连波等[5]考虑公交站点与轨道车站“多对多”情形，建立基于换乘网络的接驳线网优化模型．近年来，针对公交接驳线网优化问题，许多学者采用遗传算法进行求解．LI等[6]提供可以降低乘客到达接驳公交成本的接驳公交调度模型，并利用遗传算法求解大型线网．SUN等[7]以搜寻基于总出行时间最小化的接驳公交路径和时刻表为目标，构建针对个人需求的定制公交优化模型．ANASTASIOS等[8]采用遗传算法求解需求响应的接驳公交最后一公里问题．TAPLIN等[9]构建基于最短步行距离到达接驳公交车站的模型，并通过遗传算法搜寻最大需求公交站点．针对FBNDP，研究多将公交站点与轨道车站之间的关系模式分为“多对一”和“多对多”的情形讨论，但公交站点仍限制在仅允许被单一线路服务．

对于与FBNDP问题类似的开放式车辆路径问题，如何构造满足需求可拆分的解是解决此类问题的关键．研究已提出一些求解方法[10]，如列生成算法[11]、禁忌搜索算法[12-14]等．

本研究受需求可拆分条件下车辆路径问题的启发，针对经典FBNDP中每一个公交站点只被单一接驳线路服务的限制问题，将其扩充至每个公交站点可以被多条公交接驳线路服务，即公交站点和公交接驳线路间具有“多对多”的关系，使之更符合实际客流分布规律．由此形成需求可拆分的公交接驳线网优化问题(feeder-bus network-design problem with split delivery, FBNDP-SD)．通过分析换乘网络总费用，建立需求可拆分情形下的公交接驳线网优化模型，针对此问题设计改进遗传算法，并分析讨论不同公交站点客流需求强度下的优化结果．

1 公交接驳线网描述

经典FBNDP满足以下假设：① 每一个公交站点只由一条公交接驳线路服务；② 每一条公交接驳线路只连接到一个轨道接驳车站；③ 所有公交接驳线路的速度和能力统一；④ 每一公交接驳线路在其上的每一公交站点停靠．

满足假设①和②时，公交站点和公交线路间是多对一情形，与实际接驳线网存在较大差别．为此，取消假设①，即允许每一个公交站点被多条公交接驳线路服务，将该问题拓展至需求在多条线路间具有可拆分性的情形，形成FBNDP-SD．

FBNDP-SD接驳线网相关的基础网络包括I个常规公交站点和J个轨道交通车站，记公交站点集合为B={1,2,…,I}， 轨道车站集合为T={I+1,I+2,…,I+J}， 网络节点集合N=B∪T． 记任意节点i、j间的距离为Lij，i,j∈N．

2 FBNDP-SD的优化建模

2.1 FBNDP-SD的构成约束

定义Xihk及Yijk表示站点间、站点和线路间关系：

i=1,2,…,I+J;h=1,2,…,I+J;k=1,2,…,K.

i=1,2,…,I;j=I+1,…,I+J;k=1,2,…,K.

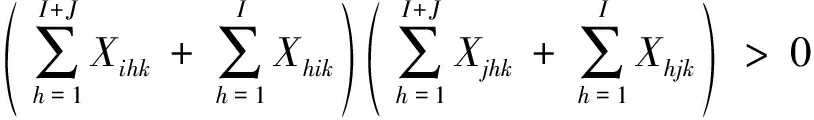
FBNDP-SD线网需要满足以下网络结构约束：

(1)

(2)

(3)

(4)

(5)

(6)

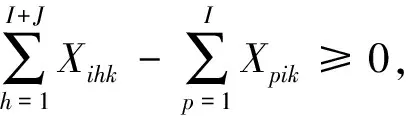
i=1,2,…,I;k=1,2,…,K

(7)

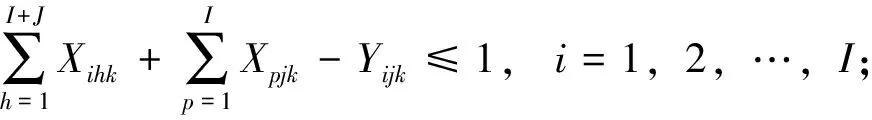
j=I+1,I+2,…,I+J;k=1,2,…,K

(8)

d=I+1,I+2,…,I+J

(9)

(10)

(11)

上述网络结构约束中，式(1)保证FBNDP-SD线网的连通性，即公交站点集合须通过接驳线路，或通过其他公交站点接续至轨道交通车站．其中，H为所有接驳轨道交通车站和部分公交站点的集合，H为N的子集．

式(2)至式(4)保证每条接驳线路的完整性，式(2)表示每条公交接驳线路仅连接1个轨道交通车站；式(3)表明接驳线路均终止于轨道交通车站；式(4)限定接驳线路至少应包含1个公交站点和1个轨道交通车站．

式(5)至式(8)为接驳线网中线路与车站的关系约束，式(5)表示需求可拆分情形下，每一公交站点至少有1条接驳线路经由；式(6)至式(7)表示同一线路上单个站点仅停靠1次，且该线路必须是一个无环的简单路；式(8)是接驳线路k与站点i、j间的关系变量Yijk约束．

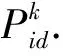
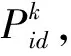
2.2 公交接驳线网优化模型

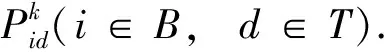
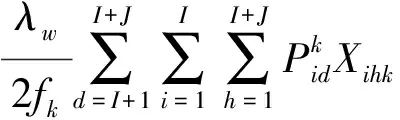
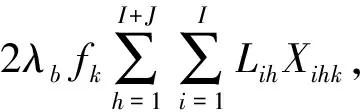
包含乘客广义出行费用和运营者运营成本的系统费用最小化优化目标函数为

(12)

其中，Zk为公交接驳线路k相关的系统费用，即

(13)

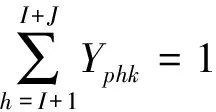
(14)

客流Pid选择线路k的客流量与换乘网络路径费用有关．以Logit分配作为客流选择函数，则该OD客流在线路k上的分配客流量为

(15)

基于需求可拆分的公交接驳线网优化模型由目标函数(12)和约束条件(1)至(11)、客流选择函数(15)以及关联函数(13)和(14)组成．与FBNDP优化模型相比，除网络结构约束变化外，还增加了线路间客流选择函数(15)．

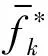
(16)

其中，Pk和Lk为第k条接驳线路的总客流需求和线路长度．相应的线路费用为

(17)

3 模型求解

FBNDP具有多个变量及约束条件，求解方法多采用启发式算法[1]，FBNDP-SD较FBNDP更难求解，本研究采用遗传算法[15]进行求解．由于FBNDP-SD问题构解较为困难，在初始种群个体生成和交叉操作生成子代个体过程中，均是先生成FBNDP线网，再以此为基础生成FBNDP-SD线网．

对初始种群个体生成操作，首先通过选取公交站点不断扩充公交线网，形成不包含重复点的初始个体，再插入重复点形成FBNDP-SD个体，构成初始接驳线网种群，并根据客流选择规律在接驳线路间分配客流量和公交线路开行频率．对于交叉操作，针对父代双亲个体，剔除重复站点形成FBNDP个体，采用与文献[5]类似方法双亲单子生成2个FBNDP子代个体，并将剔除的重复站点按照一定插入策略随机插入FBNDP子代个体，完成FBNDP-SD子代个体的构造．具体算法流程见图1．

3.1 编码方案和适应度

公交接驳线网问题一般采用自然数编码，即采用公交车站与轨道交通车站编号表示，使站点与基因片段对应．如当B={1,2,3,4,5,6,7}，T={8,9,10}时， 某一接驳线网表示为1 2 3 8 4 5 9 6 7 10，该接驳线网由3条接驳线路组成，对应上述3个字串1 2 3 8、4 5 9及6 7 10．

以最小化目标函数的倒数为基础，考虑约束条件(11)并引入罚因子λ, 构造个体Ω的适应度函数为

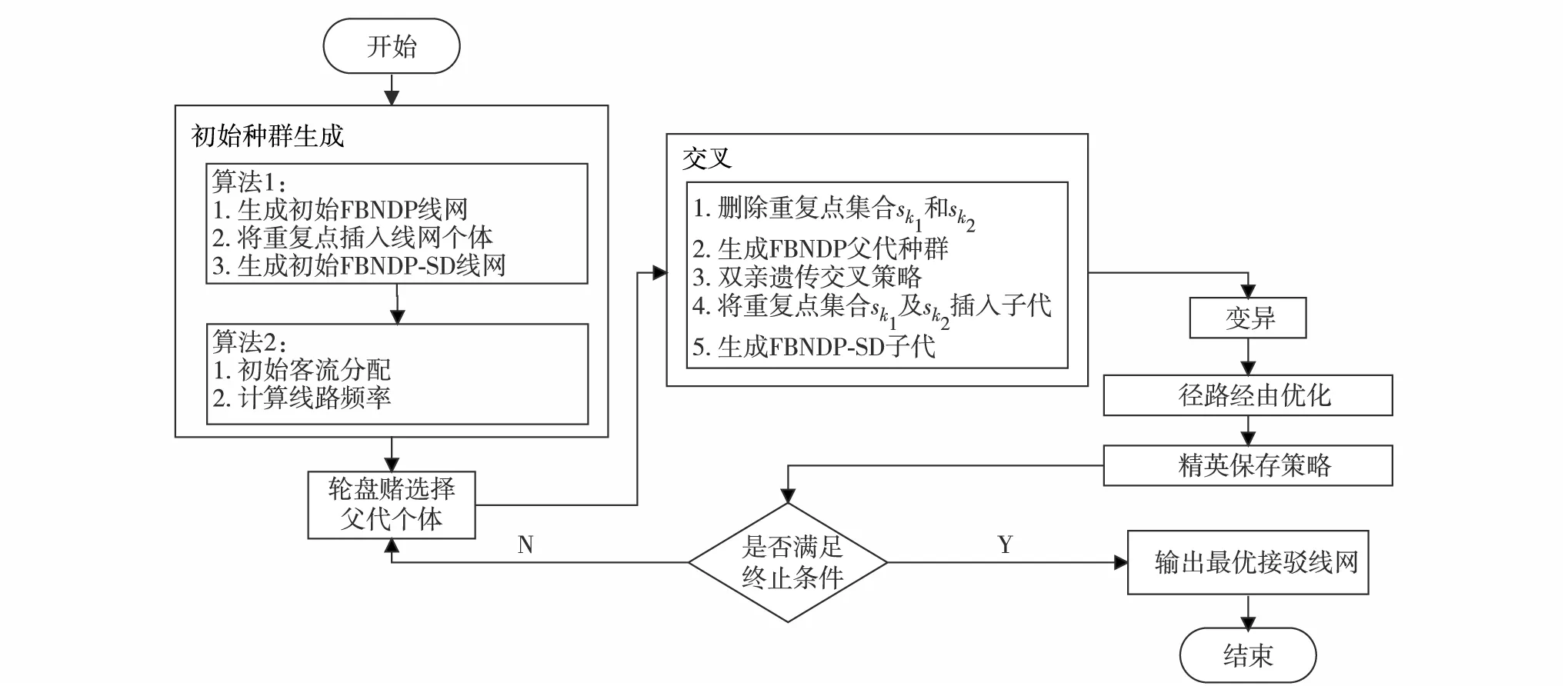
图1 算法流程图Fig.1 Framework of the proposed algorithm

3.2 初始种群生成

随机选择轨道车站，按照一定概率选择未在线网中的公交车站，将其加入该接驳车站所属的某条线路，或由该轨道车站和公交站点组成新的直连接驳线路．对于轨道车站j和公交车站i构成的直连接驳线路，可依据式(13)和式(16)，获得线路的最优系统成本DCij为

(18)

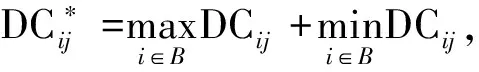
FBNDP初始线网构建完毕后，对每一公交站点尝试作为重复点，构造包含重复点的FBNDP-SD初始线网．

算法1初始FBNDP-SD线网生成算法，其步骤为

1) 置集合B′=B为构建当前接驳线路的可选择公交站集，Ω为此时的接驳线网，且线路编号k=1．

2) 若B′=φ， 转5)．否则，从T中选取1个轨道车站j， 选择方法为等概率随机选取．

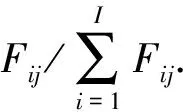
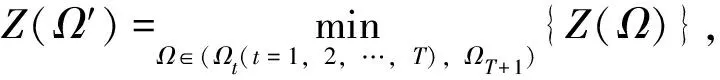
5) 对于已构造的FBNDP初始线网，采取重复点添加策略构造FBNDP-SD初始线网：对于每个公交站点i， 分别找到距离其最近，且不包含其本身的线路加入(以点到点之间的距离作为衡量)，使i点同属于不同线路，将线网转换为需求可拆分情形并记录重复点i′集合．

对每一FBNDP-SD线网，重复点在各条线路的流量分配算法见算法2．

算法2线路客流分配及频率确定算法，其步骤为

1) 已知包含重复点的初始解，其中的重复点i′为需要进行客流需求拆分的点．

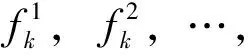
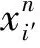
采用算法1，每次构造1个个体，直至达到初始种群规模n为止．

3.3 遗传算子设计

3.3.1 选择复制

采用2种机制增强算法搜索能力：① 竞争机制．复制n个个体的种群以产生2n个个体的种群，两两比较随机分成n对后的个体适应度，保留较优的种群规模个体；② 入侵机制．采用初始种群生成算法产生n个个体并找到其中适应度最高的ρn个个体，用于替代上述个体中适应度最低的ρn个个体，其中，ρ∈(0,1)为入侵比例，可以提前设定为常数或采用动态控制策略．

3.3.2 交叉操作

对选中的父代个体，采用双亲双子的交叉操作，其步骤为

1) 剔除双亲的重复点，形成FBNDP个体．具体对于每个重复点，比较其在各线路上的客流量，保留客流量最大的重复点并剔除该点在其他线路中的重复点．

2) 对已剔除重复点的FBNDP父代双亲个体，分别以某一父代个体为基础，采用文献[2]的双亲单子交叉操作，对于FBNDP父代个体Ωl1及Ωl2， 以Ωl1为基础，以Ωl1的首个基因位对应的公交站为起点，按顺序比较其在两个父代中下一个站点与该线路接驳轨道车站间的线路费用，保留较好点作为新生子代的基因，并以之为起点继续比较．在Ωl1和Ωl2中去除该基因，构造当前线路的结束条件为选取基因对应轨道车站．对所有公交站点重复此过程，形成子代．

3) 将两个父代个体的重复点按概率插入两个FBNDP子代个体，形成FBNDP-SD子代个体．将父代个体中的重复点作为集合，将集合中的每个重复点随机插入其中一个子代个体(为保证插入重复点的科学性和效率性，插入位置为该点所在线路外的线路上，最靠近该点的5个公交点的位置)．对重复点的各个备选插入位置，通过调用算法2计算各线路的客流量及频率，并优化备选重复点所在线路的径路经由，接受使线网费用下降程度最大的插入方案．

3.3.3 变异操作

为增强全局寻找最优解能力，以变异概率Pm随机选取基因点，并依据概率p接受较差变异解．若选中公交站点，将其随机插入到其他公交站点对应的基因位；若选中轨道接驳车站，则随机选择另一轨道接驳车站替代．对变异解需考虑其变异质量，即接受概率为[16]

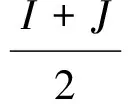
3.4 辅助优化策略

1)径路经由优化策略．对交叉操作中的子代个体，其每一条接驳线路均需优化其径路经由．单条接驳线路的径路经优化后均可视为一个具有固定终点的车辆路径问题．采取在线路内部随机挑选2个公交站点i和j进行单点交换的方法逐步优化线路径路．

2) 精英保存策略．每次产生新一轮满足种群规模的子代后，将本轮最优解与历史最好解比较并保留二者中较优解．

3.5 终止条件

算法终止于达到最大进化代数Tmax或目标函数值在T′代内收敛．

4 算例分析

采用文献[5]构造的通用算例网络，包含80个公交站点和4个轨道车站．遗传算法中设置种群规模为100，交叉概率为0.8，变异概率为0.08，最优个体保持代数为120，最大进化代数为1 500．采用C#语言编程，并分析不同客流需求强度下的优化结果．模型参数见表1．

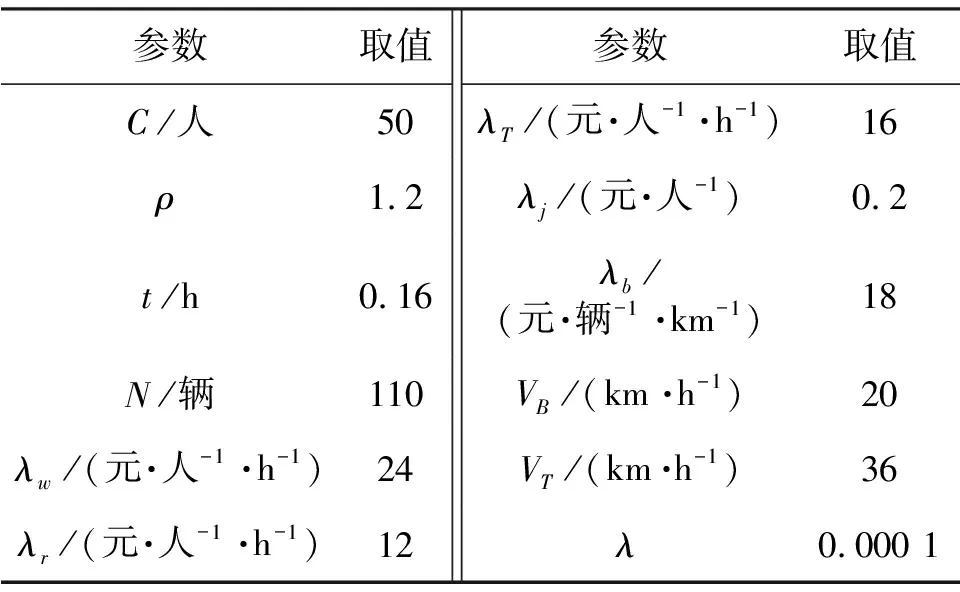
表1 模型参数

4.1 固定客流强度下的优化结果

考虑每个公交站点与各轨道车站均有客流需求且客流分布均等．单位时段内公交站的客流需求强度为200人．最优接驳线网如图1．其中，接驳线路数22条，平均长度1.70 km．线路每小时开行频率为13.54．接驳线网方案存在1个重复点，为40号站点．系统总费用为53 273元．旅客乘坐公交时间与旅客乘坐列车时间比值为1.20∶0.81，旅客绕行比为1.25．

FBNDP-SD最优线网与文献[5]中FBNDP结果的对比见表2，系统总费用的降低了0.03%．可见，在相同线网规模及轨道车站客流分布等条件下，允许需求可拆分情形时，接驳线网方案更为优化合理，线路长度略有减少，但开行频率维持不变．由于问题的复杂性大大增加，使得运算时间显著增加．

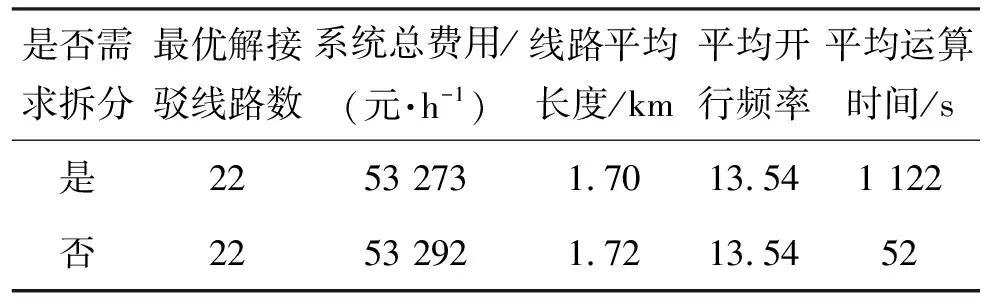
表2 需求拆分与否条件下的最优接驳线网对比

4.2 站点客流需求差异的优化结果

上述算例中每个公交站点客流需求强度在接驳线网中的地位一致，且公交站点客流需求在轨道交通站点之间均匀分布，接驳线路交叉关系并不明显．为对比不同客流需求下的线网结果，对公交站点采取在50～400人按50的倍数随机设置单位时段客流需求，并且每个公交站点与轨道交通站点间的客流呈线路两头大中间小的不均匀分布，与4个轨道交通车站间客流比例分别为40%、10%、10%及40%，考察FBNDP-SD线网的变化规律．

求得的最优接驳线网如图2与图3(站点编号右下角标表示客流需求)．其中，接驳线路24条，平均长度为1.74 km．线路每小时开行频率为13.96．系统总费用为60 980 元．接驳线网方案存在8个重复点，分别是26、19、20和79号站点，其中，19号公交站点重复5次，这些站点的客流需求均为200 人或300 人．

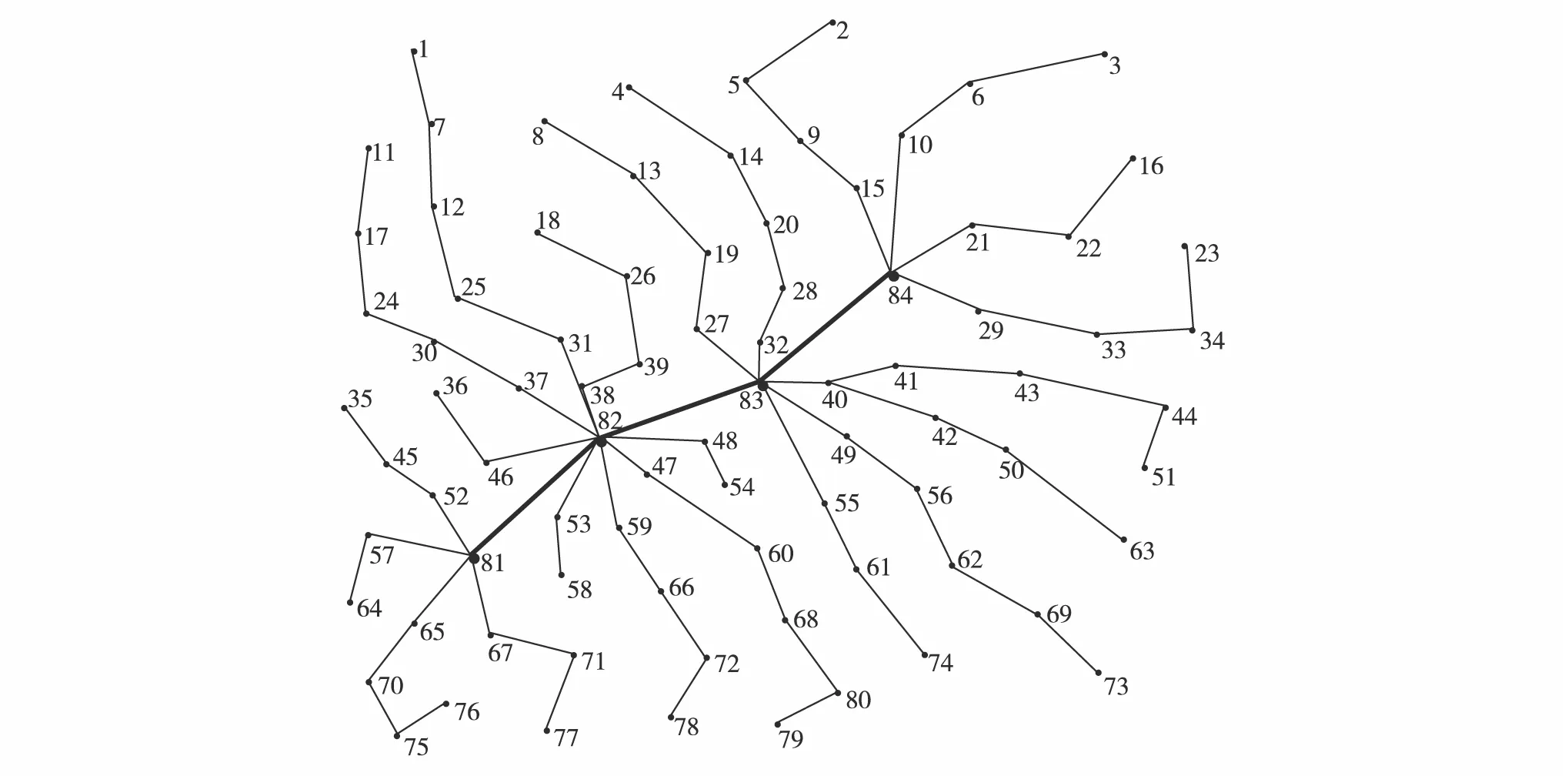
图2 固定客流强度下的最优接驳线网Fig.2 Best result under constant flow volume

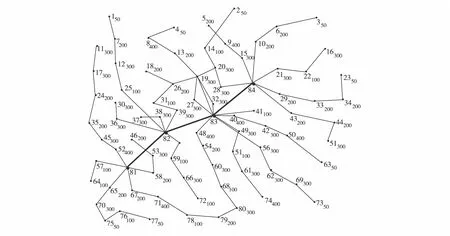
图3 站点客流需求差异的最优接驳线网Fig.3 Best result under varying flow volume

与固定客流强度下的优化结果相比，重复点的数量随整体网络客流强度的增大由1个增加到8个，重复站点设置更倾向于客流较多的站点．

在相同线网条件下，需求可拆分情况下FBNDP-SD最优线网与不考虑需求可拆分条件的FBNDP最优线网各项指标对比见表3．其中，表3第2行表示不考虑需求可拆分条件的公交接驳最优线网结果．通过表3可知，系统总费用降低比率达到0.61%，与固定客流强度下的优化结果(0.03%) 对比， 费用降低效果更为明显，且线路平

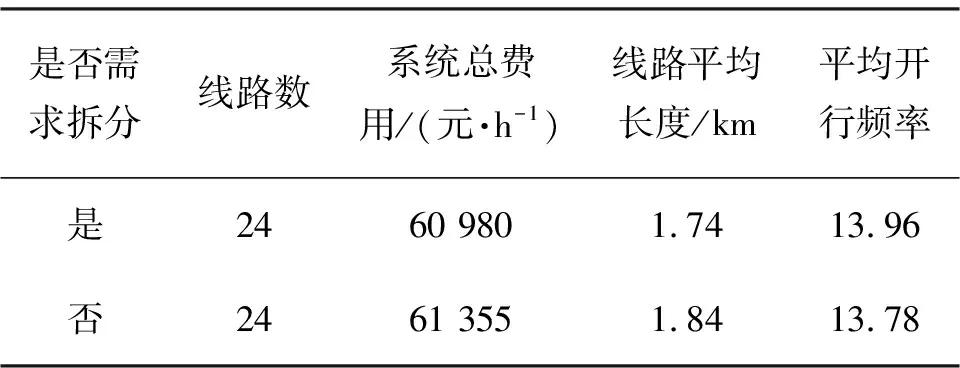
表3 需求拆分与否条件下的最优接驳线网各项指标对比

均长度减少，开行频率略有上升．考虑需求可拆分情形可降低线路的平均长度，为乘客提供更多的线路选择，说明在客流需求量大的情况下，允许需求拆分、多条线路共同为某些需求量大的站点提供服务， 对降低网络费用、 优化线网结构更具实际意义．

结 语

本研究针对经典FBNDP，进一步放宽假设条件，允许需求在线路间拆分，使公交站点可以为多条公交接驳线路服务，建立基于换乘网络且满足需求可拆分的公交接驳线网优化模型．根据模型特点设计了基于遗传算法的求解方法．模型和算法综合考虑需求可拆分条件下的网络结构和客流选择行为等约束条件；在优化算法中，以FBNDP的解为基础，融入重复点的生成和插入策略，实现FBNDP解和FBNDP-SD解的相互转换，有效解决了FBNDP-SD构解困难的问题．优化结果表明，在考虑公交需求可拆分的情形下，FBNDP-SD线网能够为公交站点提供多条接驳线路进行选择，从而有效分流乘客，降低线路成本，优化线网结构．对于线网客流强度较高的情况或者具有较大客流量的站点，考虑公交需求可拆分更具实际意义．