素数略探

杨尚文

【摘要】自然数包括1、素数（质数）与合数.本文将素数之外的自然数用“非素数”表示，以区别对待.当自然数大于10时，可以从自然数的个位数的性质出发，来确定一个自然数是否为非素数，文中对个位数为1，3，7，9的自然数中存在着的非素数进行讨论，通过对其因子的个位数的限定讨论，来探知其存在的规律，从而为对非素数分布的研究以及对素数分布的研究提供一点思路.

【关键词】非素数;素数;个位数;因子

本文将对素数稍做研究，如有错误之处还请读者指正.

一、先把自然数排成十列（如表1）

二、素数之外的自然数，包括1和合数这两部分非素数

以下论述，有三个前提如下：

① 从1到10的自然数，忽略不计;

② 文中，1和非素数本身不作为因子考虑;

③ 很明显，一个非素数（大于10），不管其可以表示为多少个因子相乘，最终都可以表示为2个因子相乘.

以下描述中，a，b，c，d，e，f，g，h为“0”或自然数.

以下描述中，以a1为例，则，a1=11，21，31，41，….

据此，展开探讨.

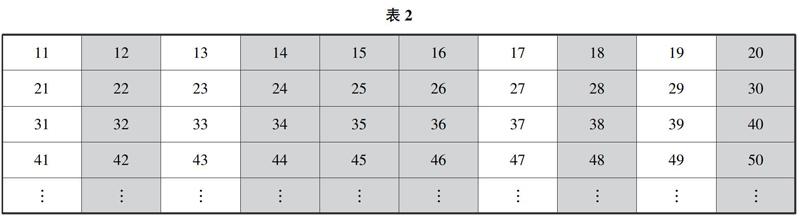
1.很明显，个位数为2，4，5，6，8，0的自然数都是非素数，用灰色底表示，如表2.

2.再来看个位数为1，3，7，9的自然数

分别针对个位数为1，3，7，9的自然数，从其个位数出发进行讨论，可以看出：

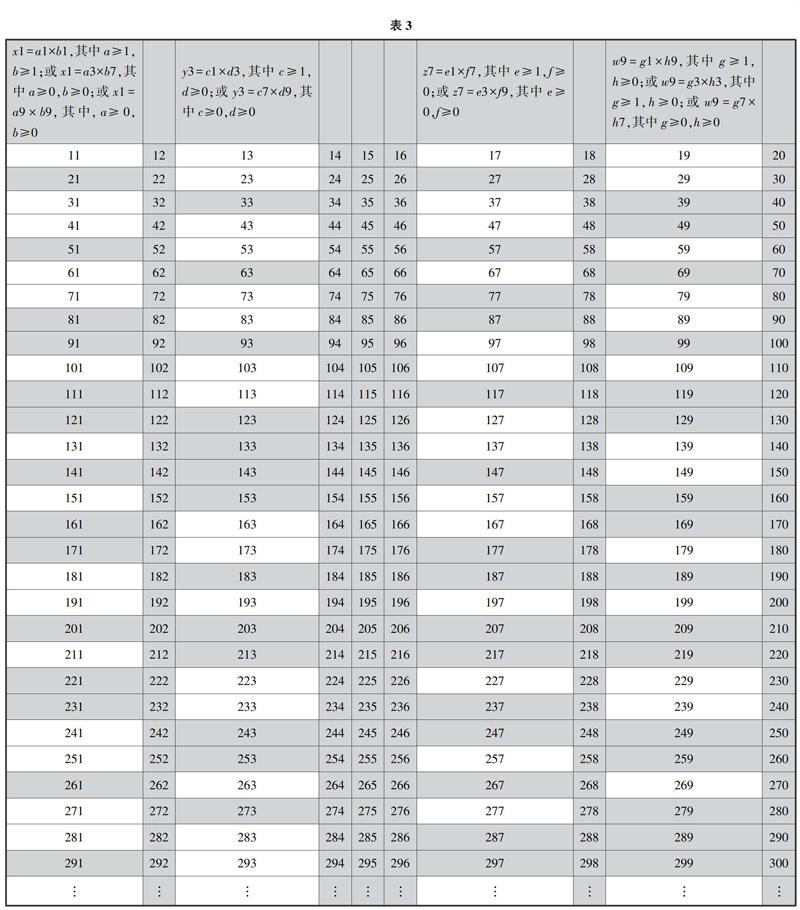
（1）个位数为1的非素数X，记为x1，若用x1=A×B表示，则除了自然数1之外，A和B的个位数只能是1，1或3，7或9，9.将A和B分别记作a1，b1或a3，b7或a9，b9，于是得到x1=a1×b1，其中a≥1，b≥1;或x1=a3×b7，其中a≥0，b≥0;或x1=a9×b9，其中，a≥0，b≥0.

（2）个位数为3的非素数Y，记为y3，若用y3=C×D表示，则除了自然数1之外，C和D的个位数只能是1，3或7，9.将C和D分别记作c3，d7或c7，d9，于是得到y3=c1×d3，其中c≥1，d≥0;或y3=c7×d9，其中c≥0，d≥0.

（3）个位数为7的非素数Z，记为z7，若用z7=E×F表示，则除了自然数1之外，E和F的个位数只能是1，7或3，9.将E和F分别记作e1，f7或e3，f9，于是得到z7=e1×f7，其中e≥1，f≥0;或z7=e3×f9，其中e≥0，f≥0.

（4）個位数为9的非素数W，记为w9，若用w9=G×H表示，则除了自然数1之外，G和H的个位数只能是1，9或3，3或7，7.将G和H分别记作g1，h9或g3，h3或g7，h7，于是得到w9=g1×h9，其中g≥1，h≥0;或w9=g3×h3，其中g≥1，h≥0;或w9=g7×h7，其中g≥0，h≥0.

以上所有的X，Y，Z，W这些非素数（大于10），包含了个位数是1，3，7，9的所有非素数（大于10），用灰色底表示（如表3）.

表3中，若取自然数11～300为区间，便得到区间内所有非素数，并到得到区间内所有素数.

3.同理，对于自然数，将X，Y，Z，W包括的非素数（大于10）集合，加上1，4，6，8，9，10这六个数，得到自然数中的全部非素数（如表4）.

四、综上，略做一些归纳

（一）可以看出，非素数（大于10）只存在于个位数为1，3，7，9的自然数中，而由于个位数为2，4，5，6，8，0的自然数都是非素数，于是，素数（大于10）也只存在于个位数为1，3，7，9的自然数中.

（二）可以看出，非素数（大于10）有一定的分布规律可循，以“y3=c1×d3，其中c≥1，d≥0”为例，用灰色底表示如表5：

1.当d=0时，y3=c1×3，可以看出，每3格出现一个非素数;

2.当c=1时，y3=11×d3，可以看出，每11格出现一个非素数;

3.当d=1时，y3=c1×13，……

可以看出，非素数的分布存在一定的规律，可以较为简便地通过设置合适的计算机程序得到非素数.

（三）可以看出，对于非素数（大于10），既然只存在于个位数为1，3，7，9的自然数中，并且x1，y3，z7，w9各自的计算逻辑比较清晰，于是，求得非素数的计算就显得比较确定，特别是在给定的有限的自然数范围内，非素数的计算显得比较便捷.

（四）从非素数的因子组成和相互关系，依靠坐标系，可以进一步研究其几何分布范围和界限等，这可以为素数几何分布范围和界限问题的研究提供便利.