基于SOLO分类理论的试题思维水平评价研究

陈彤`

【摘要】SOLO分类理论将思维分成单点结构水平、多点结构水平、关联结构水平及抽象扩展结构水平.以该理论为评价框架，通过分析试题思维水平在试题数量、题型及考查内容上的分布，评价近两年高考理科数学全国卷试题的思维水平.研究发现，近两年高考理科数学全国卷对学生思维综合概括能力的要求由高到低依次为全国Ⅰ卷、全国Ⅱ卷、全国Ⅲ卷.通过评价近两年高考理科数学全国卷试题的思维水平得出如下启示：教师应培养学生综合解决问题的能力、从思维水平上把握高考试题命题规律，依据SOLO分类理论开展教学评价.

【关键词】SOLO分类理论;思维水平;试题;理科数学

【基金项目】课题类别：沈阳师范大学师范专业认证专项课题;课题编号：JG2018-ZX03;课题名称：师范专业认证背景下“课程目标达成度”评价实践的改进研究

自1977年恢复高考以来，高考一直是社会关注的焦点.为了提高国民素质、培养并选拔能够担起民族复兴大任的时代新人，我国在不断地进行教育改革.数学是自然科学的重要基础，在形成人的理性思维、科学精神和促进个人智力发展的过程中发挥着不可替代的作用.彼格斯將人在实际回答某个问题时表现出来的思维结构称之为“可观察的学习成果结构”（Structure of the Observed Learning Outcome，简称SOLO）.“可观察的学习成果结构”又可分成不同层次的思维水平.教师将SOLO分类理论对水平思维的划分具体应用到高考试题对学生思维水平的检验上，分析当下高考理科数学试题对学生思维水平的要求，可在思维水平上把握命题规律，提高自身教育教学水平.

一、SOLO分类理论下试题思维水平分类

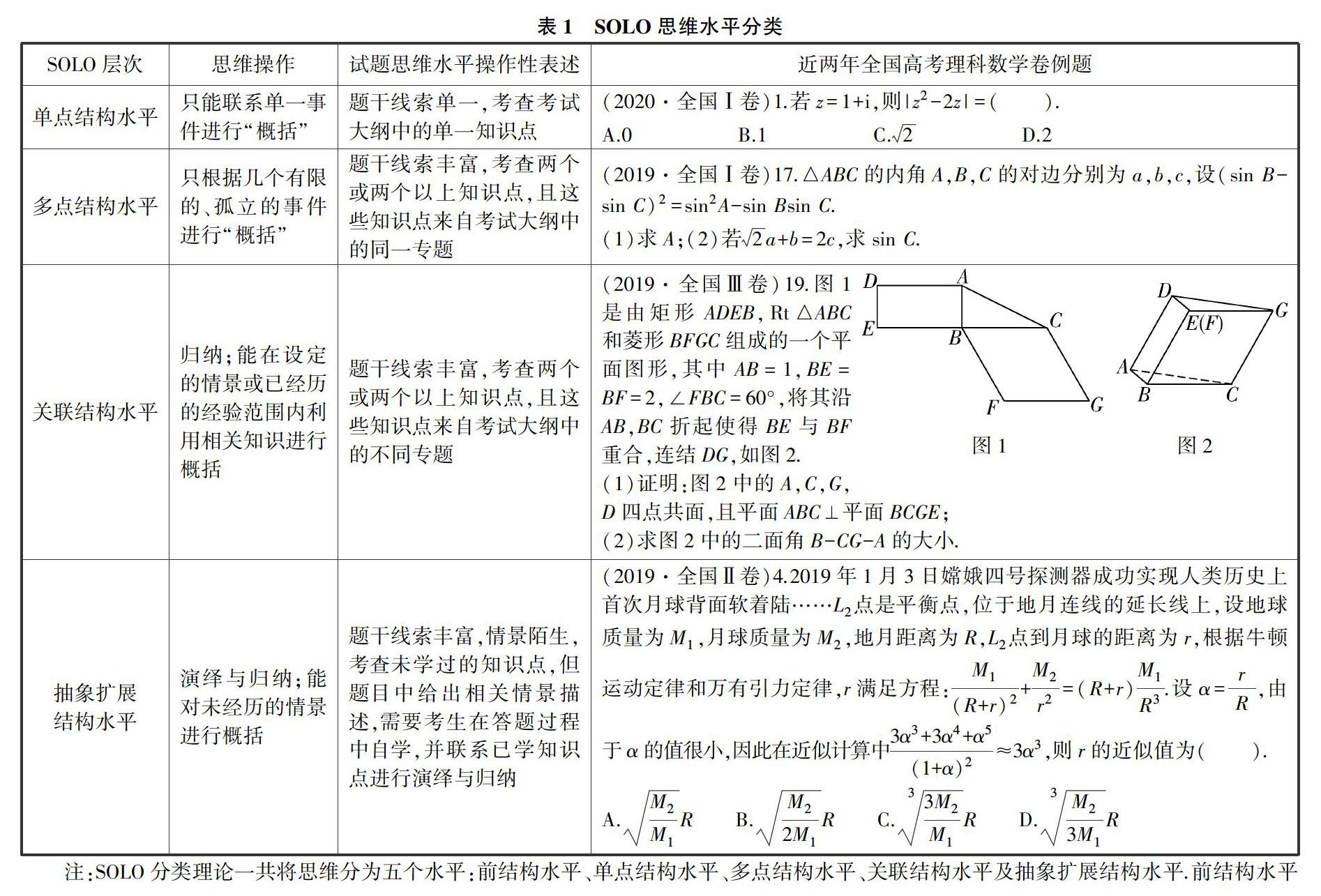
在认知心理学领域中，知识是对信息的表征.试题是陈述性知识，根据信息加工理论，陈述性知识可看成由一些有时称之为组块的基本认知单元组成.组块表征了人们已学到的某些信息.时间序列、表象、命题则是三种组块类型.考生在阅读试卷的过程中，将信息编码为命题，多个命题组块形成命题网络.我们以知识点作为划分思维水平的主要依据，并结合SOLO分类理论，将解决数学题时考查的思维水平分为单点结构水平、多点结构水平、关联结构水平及抽象扩展结构水平（见表1）.“思维操作是指把线索和回答联系起来的方式”，在学生解题时的思维操作过程中，“线索”对应试题的题干所给信息，“回答”对应试题考查的知识点，即学生解题时需要应用的知识点.

（1）求A;（2）若2a+b=2c，求sin C.

关联结构

水平

归纳;能在设定的情景或已经历的经验范围内利用相关知识进行概括

题干线索丰富，考查两个或两个以上知识点，且这些知识点来自考试大纲中的不同专题

（2019·全国Ⅲ卷）19.图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个  图1  图2平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2.

（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE;

（2）求图2中的二面角B-CG-A的大小.

注：SOLO分类理论一共将思维分为五个水平：前结构水平、单点结构水平、多点结构水平、关联结构水平及抽象扩展结构水平.前结构水平表示“拒绝，同义反复，转换，跳到个别细节上”，是思维混乱的状态，由于高考具有严谨性与科学性，其试题考查的思维水平不存在前结构水平，故在此省略对前结构水平的分析.

二、SOLO分类理论下理科数学试题思维水平评价

（一）全国Ⅰ卷试题思维水平评价

在试题数量上，经统计，近两年全国Ⅰ卷试题考查的思维水平处于单点结构水平的有10题，共计50分;处于多点结构水平的有16题，共计106分;处于关联结构水平的有18题，共计147分;处于抽象扩展结构水平的有2题，共计17分.研究发现，全国Ⅰ卷试题对四种思维水平均进行了考查，其中处于多点结构水平与关联结构水平的题目占比较高.

在试题题型上，全国Ⅰ卷的试题在选择题上，对四种思维水平均有所考查;在填空题上，考查思维水平涉及多点结构水平与关联结构水平;在简答题上，考查的思维水平涉及单点结构水平、多点结构水平及关联结构水平，且集中于关联结构水平.总的来说，全国Ⅰ卷的选择题大多考查思维的单点结构水平与多点结构水平，填空题主要考查思维的多点结构水平与关联结构水平，简答题倾向于考查思维的关联结构水平.

在试题考查内容上，

统计全国Ⅰ卷考查内容对应的专题在各思维水平上出现的次数，将出现次数为两次及以上的专题作为试卷主要考查内容.在全国Ⅰ卷中，处于单点结构水平的试题，考查内容主要涉及集合、复数以及计数原理;处于多点结构水平的试题，考查内容主要涉及基本初等函数Ⅰ、数列;处于关联结构水平的试题，考查内容主要涉及基本初等函数Ⅰ、导数、立体几何、解析几何、圆锥曲线、向量、概率统计以及选考内容中的不等式;处于抽象扩展结构水平的试题，考查内容主要涉及数列与概率统计.研究发现，处于关联结构水平的试题考查面较广.

（二）全国Ⅱ卷试题思维水平评价

在试题数量上，经统计，全国Ⅱ卷试题考查的思维水平处于单点结构水平的有8题，共计40分;处于多点结构水平的有19题，共计180分;处于关联结构水平的有9题，共计73分;处于抽象扩展结构水平的有4题，共计27分.研究发现，全国Ⅱ卷试题对四种思维水平均进行了考查，其中处于多点结构水平的试题数及所占分值均为最高.

在试题题型上，全国Ⅱ卷的试题在选择题上，对四种思维水平均有所考查，其中多点结构水平占半数，其他三种思维水平分布较为平均.在填空题上，对四种思维水平均有所考查，其中对多点结构水平的考查最多;在简答题上，考查的思维水平未涉及单点结构水平，主要集中在多点结构水平，其次是关联结构水平，对抽象扩展结构水平进行考查的较少.经统计，全国Ⅱ卷的选择题与简答题倾向于考查处于多点结构水平的思维，而填空题考查的思维水平则较为平均.

在试题考查内容上，统计全国Ⅱ卷考查内容对应的专题在各思维水平上出现的次数，将出现次数为两次及以上的专题作为试卷主要考查内容.在全国Ⅱ卷中，处于单点结构水平的试题，考查内容主要涉及计数原理;处于多点结构水平的试题，考查内容主要涉及函数、向量、概率统计、解析几何、解三角形以及数列，选考题考查的思维水平均处于该水平;处于关联结构水平的试题，考查内容主要涉及函数、几何、圆锥曲线以及逻辑用语.研究发现，处于多点结构水平与关联结构水平的试题考查面较广.

（三）全国Ⅲ卷试题思维水平评价

在试题数量上，

经统计，全国Ⅲ卷试题考查的思维水平处于单点结构水平的有13题，共计65分;处于多点结构水平的有25题，共计187分;处于关联结构水平的有8题，共计68分.研究发现，全国Ⅲ卷试题考查的思维水平涉及单点结构水平、多点结构水平及关联结构水平，未涉及抽象扩展结构水平，其中处于多点结构水平的试题数及所占分值均为最高.

在试题题型上，全国Ⅲ卷的试题在选择题上，仅考查了前三种思维水平;在填空题上，考查的思维水平涉及单点结构水平与多点结构水平，分值大致相当;在简答题上，考查的思维水平涉及多点结构水平与关联结构水平，其中对多点结构水平的考查偏多.经统计，全国Ⅲ卷选择题考查的思维水平在前三种水平上的分布较为平均，填空题和简答题主要考查处于多点结构水平的思维，各题型均未考查处于抽象扩展结构水平的思维.

在试题考查内容上，统计全国Ⅲ卷考查内容对应的专题在各思维水平上出现的次数，将出现次数为两次及以上的专题作为试卷主要考查内容.在全国Ⅲ卷中，处于单点结构水平的试题，考查内容主要涉及集合、复数与计数原理;处于多点结构水平的试题，考查内容主要涉及函数、几何、解三角形以及数列，并且选考题考查的思维水平均处于该水平;处于关联结构水平的试题，主要考查内容与多点结构水平相似.研究发现，处于多点结构水平与关联结构水平的试题考查面较广.

三、结论与启示

比较全国Ⅰ卷、Ⅱ卷、Ⅲ卷试题考查的思维水平，发现其对学生思维综合概括能力的要求由高到低依次为全国Ⅰ卷、全国Ⅱ卷、全国Ⅲ卷.通过评价近两年高考理科数学全国卷试题考查的思维水平得出如下启示：

第一，教师要培养学生解决综合问题的能力.在近两年理科数学全国卷的试题中，超过半数的试题考查的思维水平处于多点结构水平与关联结构水平，还有少数试题考查的思维水平处于抽象扩展结构水平，属于“拔高题”，这类试题重点考查学生的思维概括能力.因此，教师在教学中应注重培养学生解决综合问题的能力，提高学生的思维水平，加强学生對知识之间联系的认识，并且培养学生用多种方法解决问题.第二，教师要从思维水平上把握高考试题命题规律.分析连续两年全国卷对计数原理、复数的考查都处于单点结构水平;对数列、坐标系与参数方程、不等式选讲的考查处于多点结构水平;对函数概念与基本初等函数Ⅰ、立体几何初步、平面解析几何初步、圆锥曲线与方程、空间向量与立体几何、导数及其应用的考查处于关联结构水平.教师可根据理科数学高考试题对各专题内容在思维水平上的考查情况，在今后的课堂教学中有所侧重.第三，依据SOLO分类理论开展教学评价.教学评价可以检验教学效果以及教学目标的达成度，是教学必不可少的环节.SOLO分类理论为教师进行教学评价提供了良好的理论参考.在课堂的教学评价中，教师可根据学生的回答，判断学生对该问题的理解所处的思维水平状态.在阶段性的总结性评价中，教师可以编制不同思维水平的试题考查学生阶段性的学习效果.这样有助于教师全面把握学生的学习情况，进而更有针对性地开展教学.

【参考文献】

[1]中华人民共和国教育部.普通高中数学课程标准：2017年版[M].北京：人民教育出版社，2018.

[2]约翰·B.彼格斯，凯文·F.科利斯.学习质量评价：SOLO分类理论（可观察的学习成果结构）[M].高凌飚，张洪岩，译.北京：人民教育出版社，2010.

[3]托马斯·费兹科，约翰·麦克卢尔.教育心理学：课堂决策的整合之路[M].吴庆麟，译.上海：上海人民出版社，2008.