画“双圆”解匀强磁场中带电粒子扫射问题

陈卫国

摘   要：“图像法”是解决物理问题的一种重要方法。通过画“双圆”解决圆域磁场、单边界磁场中带电粒子扫射问题，形象、直观、有效。

关键词：双圆;匀强磁场;带电粒子;扫射

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2020）01-0063-2

匀强磁场中带电粒子扫射问题，实质为动态轨迹圆问题，过程抽象，分析、综合能力要求较高，是学生学习“带电粒子在磁场中运动”的难点。图像法画双圆处理，化抽象为形象，处理简洁。分为两种磁场：圆域磁场和单边界磁场。

1    圆域磁场

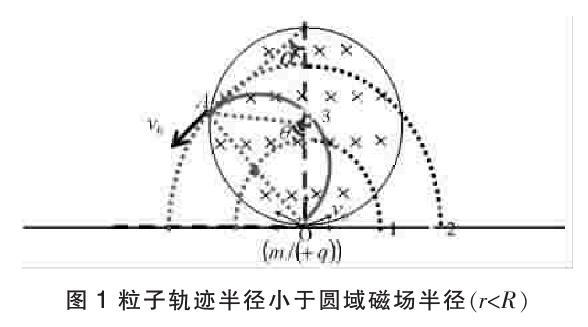
物理原型：圆域磁场半径为R，其中有垂直平面的匀强磁场B，O为磁场边界上最低点。大量质量为m、电荷量为q的带正电粒子，以相同的速率从O点射入磁场区域，速度方向沿位于纸面内的各个方向，粒子轨迹半径为r，分析粒子射出圆域磁场的情况。分为两类：

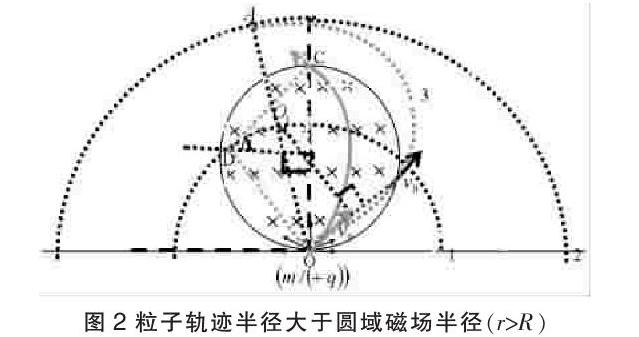
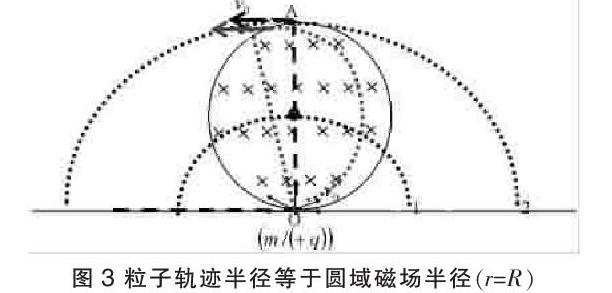
1.粒子轨迹半径小于圆域磁场半径（r

步骤：

（1）粒子从O点水平向右射出时，将在磁场中做完整的圆周运动。扫射的粒子能从圆域磁场的左半圆中部分区域射出磁场。

（2）以O点为圆心，以r为半径画圆（如图1中的圆1）;以O点为圆心，以2r为半径画圆（如图1中的圆2）。连接O和圆2上的任意点皆为可能的轨迹圆的一条直径，皆可在圆域磁场中画出轨迹圆的一部分（粒子射出磁场将做直线运动）。

（3）连接O点和圆2与圆域磁场的交点A，即为粒子在磁场中完成的最大圆弧（半圆轨迹3）。

结论：粒子从磁场中射出覆盖区域为劣弧OA段，如图1。有sinα=，得α=arcsin，并且θ=2α=2arcsin，劣弧lOA=Rθ=R·（2arcsin）。粒子水平向右射出，将在磁场中做完整的圆周运动，轨迹直径在过O点的竖直方向。粒子在磁场中耗时最长为T=。

2.粒子轨迹半径大于圆域磁场半径（r>R）时，如图2。

步骤：

（1）以O点为圆心，以r为半径画圆（如图2中的圆1）;以O点为圆心，以2r为半径画圆（如图2中的圆2）。连接O和圆2上的任意点皆为可能的轨迹圆的一条直径，皆可在圆域磁场中画出轨迹圆的一部分（粒子射出磁场将做直线运动）。

（2）过O点竖直向上作圆域磁场直径与圆域磁场交于C点，连接O点和C点，作中垂线与圆1交于D点，劣圆弧OC对应的圆心角即为粒子在磁场中做部分圆周运动耗时最长。

（3）连接O点和圆域磁场边界的任意点，作中垂线，皆与圆1有一个交点，皆可在圆域磁场中描出轨迹圆的一部分（如圆3）。故粒子可以从圆域磁场上的任意点射出。

结论：粒子水平向右射出，将向右做直线运动，粒子在圆域磁场中的轨迹只有部分圆周运动。粒子在磁场中耗时最长为轨迹圆弧在磁场中对应最长的弦OC，有sinθ=，得出耗时t=·=

3.粒子轨迹半径等于圆域磁场半径（r=R）时，“带电粒子在磁场中做圆周运动，并且，粒子将从圆域磁场的左半圆边界水平射出（粒子从O点水平向右射出时，将在磁场中做完整的圆周运动，并且轨迹圆与圆域磁场边界完全重合），如图3。

步骤：以O点为圆心，以r为半径画圆（如图3中的圆1）;以O点为圆心，以2r为半径画圆（如图3中的圆2）。连接O和圆2上左半圆的任意点皆为可能的轨迹圆的一条直径，皆可在圓域磁场中画出轨迹圆的一部分（粒子射出磁场将做水平直线运动）。

结论：粒子水平向右射出，将以半径R做圆周运动，轨迹与圆域磁场完全重合。粒子在磁场中耗时最长T=

拓展：磁发散和磁会聚。

如图4，速率相等的带电粒子射入圆域磁场，粒子轨迹半径等于圆域磁场半径（r=R）时，从某点射入的粒子将平行射出;平行射入的粒子会聚到一点。

2    单边界磁场

物理原型：有垂直平面的单边界匀强磁场B，其中有一点S，在磁场中距离磁场边界距离d。大量质量为m、电荷量为q的带正电粒子，在磁场中S点以相同的速率垂直磁场向各个方向扫射，粒子轨迹半径为r（如图5），试分析粒子运动情况;（边界上哪些位置有粒子射出;粒子从磁场边界冲出时，在磁场中的耗时情况。）

分为两类：

1.粒子轨迹直径满足2r

2.粒子轨迹直径满足2r>d时，带电粒子在磁场中做圆周运动。并且，所有轨迹圆周共S点。

（1）以S为圆心，以r为半径画圆，此为可能的轨迹圆的圆心轨迹（图5中的圆1）;以S为圆心，以2r为半径画圆，此为可能的轨迹圆直径另一端头轨迹（图5中的圆2）。

（2）过O点作长度为r的向上垂线，将垂线向左、右平移至与圆1相交，交点为C1、C2，此为粒子将不从边界射出的轨迹圆的临界圆心，对应的轨迹圆为图5中的圆3和图5中的圆4。图中D1与D2之间的长度即为粒子将从边界上射出的区域，有：

lD1D2=2×rsinα=2×r=2×r

（3）粒子能冲出磁场，在磁场中耗时最长轨迹如图5中的圆3部分，t=·

在磁场中耗时最短为轨迹图5中的圆4部分，t=·

参考文献：

[1]人民教育出版社，课程教材研究所，物理课程教材研究开发中心.物理选修3-1[M].北京：人民教育出版社，2017：6.

[2]孙翔峰.匀强磁场中的临界极值和多解问题[J].创新方案，2018（8）：163.

（栏目编辑    罗琬华）