基于SURF特征的侧扫声呐图像精确镶嵌

何复亮，伍 梦，龙睿捷，陈志高

（1.江西省中核测绘院，江西 南昌 330096；2.东华理工大学 测绘工程学院，江西 南昌 330006）

侧扫声呐使用声波作为目标探测的信息载体，通过近距离的精细探测，能够获取目标区域高分辨率的海底地貌图，已成为水下探测最主要的应用系统之一。但在实际探测过程中，容易出现因近距离探测而丢失视野以及探测较大目标时无法获取完整的场景信息的现象。针对这些问题，图像拼接技术脱颖而出。

1988年，Harris C等[1]提出了Harris角点检测算法。通过二阶矩阵的特征值检测图像上的特征点；1998年Lindeberg引入了自动尺度选择的概念，可以检测图像中具有自身尺度特征的特征点，从而使其提取的特征具有尺度不变性[2]；2003年，Matthew B等[3]在SIFT特征提取算法的研究基础上提出了基于尺度不变特征点的自动全景拼接技术。2008年，Herbert B等[4]提出了一种新的尺度旋转不变特征检测算法—SURF算法。但由于侧扫声呐图像的诸多特性以及拼接算法的复杂性，声呐图像拼接技术仍处于起步阶段，针对声呐图像还没有提出一种准确、高效的拼接方法。如何精准、实时地完成水下图像拼接，成为目前水下图像拼接算法研究的主要难点[5]。基于此问题，本文采用SURF算法进行程序设计，通过对多种方法的实验分析比较，实现了侧扫声呐图像的精确镶嵌。

1 基于SURF的侧扫声呐图像镶嵌算法

SURF算法在SIFT算法的基础上改进了特征的提取和描述方式，执行速度快、信息量小、匹配精度高、提取的特征不受光照变化、透视、仿射、旋转等影响，对于相同场景、不同尺度、不同拍摄角度的声呐图像镶嵌非常适用[6]。其最大优点在于引入了Haar特征以及积分图像的概念，解决了SIFT算法效率低的问题，在图像的识别、配准与拼接等方面得到广泛的运用。SURF算法是在积分图像的基础上进行计算，通过Hessian矩阵检测子来检测特征点；构建相同层数的尺度空间若干组，初步确定关键点；通过计算每个特征点的Haar小波变换来确定特征点描述符需先确定特征点的主方向。SURF算法简化近似思想与SIFT算法类似[7]，通过对DOH中的高斯二阶微分模板近似简化，促使滤波仅需进行加减法即可实现，这种运算与滤波模板尺寸有关。SURF算法大致步骤分为积分图像计算、特征点检测与描述、特征点匹配[8]。本文在此基础上引入了USM图像锐化、误匹配点剔除以及小波融合法，实现了声呐图像精确镶嵌。示意图如图1所示：

图1 基于SURF的侧扫声呐图像精确镶嵌示意图

2 误匹配点剔除算法

利用 SURF算法获取侧扫声呐相邻条带特征点后，需要进行特征点匹配。本文采用基于欧式距离的最近邻次近邻法进行特征点匹配。由于在高维向量空间中进行特征匹配数量巨大，过程复杂繁琐且存在成像角度及集合变形等因素影响，误匹配点是不可避免的，因此要想获取高精度的匹配结果，有必要对错误匹配点进行剔除。本文针对如下两类误匹配点检测方法进行研究，并选取了精度、运算时间等指标进行分析比较。

2.1 基于函数拟合的方法

基于函数拟合的方法是根据图像的大小、几何变形情况选择合适的函数模型，然后使用偏最小二乘法求解函数的系数。偏最小二乘方法（PLS）是一种由Wold H[9]于20世纪60年代提出的多元统计数据分析方法，它是一种多因变量对多自变量的回归建模方法，能够较好地解决许多以往用普通多元回归无法解决的问题。随着涉及领域的扩展，在图像降维、特征提取等方面，PLS衍生出了较多有效的算法[10-11]。

（1）F1和G1尽可能多地包含有各自变量的变异信息，即：

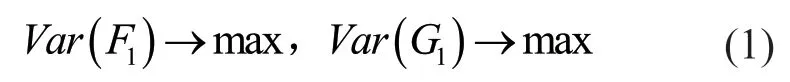
（2）F1和G1之间的相关程度达到最大，即：

式中：r(·,·)表示相关关系。

因此，将两个条件综合起来即是在PLS要求F1和G1之间的协方差达到最大，即：

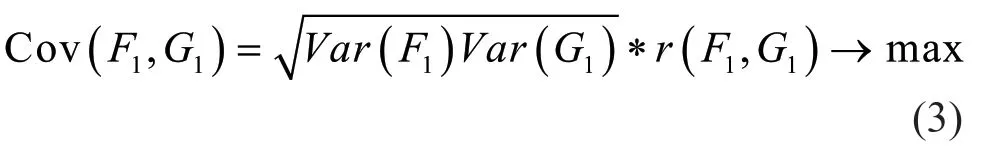
式中：Cov(·,·)表示两个变量之间的协方差。若满足上述两个条件，F1和G1不但最大可能包含变量信息，而且两者之间的相关程度达到最大。

设F1和G1是原始数据的线性变换，即：

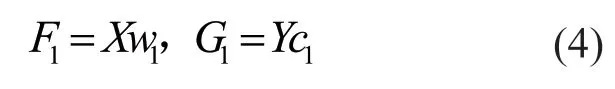
其中，w1和c1为待定的规范化投影向量。因此目标函数可以转化为：

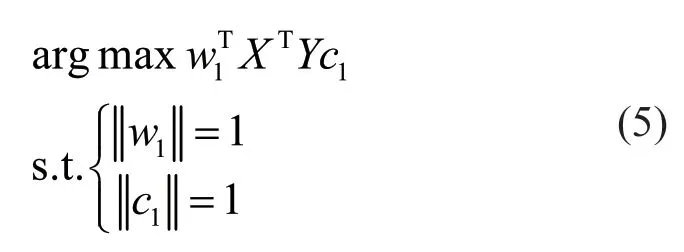
此优化问题可以通过Lagrange乘数法求解，容易得到如下特征分解问题：

求得投影向量w1和c1后，可以得到成分G1=Yc1和，其中分别表示第i对特征点在投影向量上的坐标分量。根据偏最小二乘的思想，X与Y的相关性可以近似通过F1和G1的相关性来描述。当特征点之间具有线性变换（如刚体变换和仿射变换）关系时，它们之间是严格线性相关的；当误匹配存在时，他们是近似线性相关的。通过绘制一阶成分图(F1,G1)，每对特征点i以(F1(i),G1(i))为坐标点，可以大致观察F1和G1之间是否存在显著的线性关系，当具有线性关系时，可以通过坐标点(F1(i),G1(i))拟合直线。另一方面通过观测每对特征点在成分图中的坐标位置，可以判定误匹配点对。当坐标点距离拟合直线距离远的情况下，可以认定是误匹配，由此可以定义误匹配判定准则如下：

（1）利用坐标点(F1(i)G1(i)) 拟合直线ax+by+c=0，坐标点到直线的距离为：

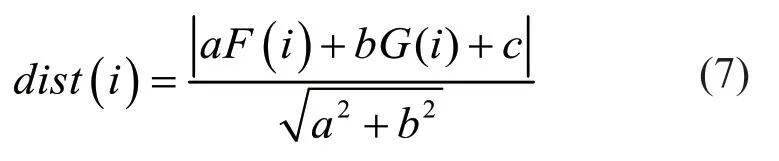
（2）定义影响函数为：

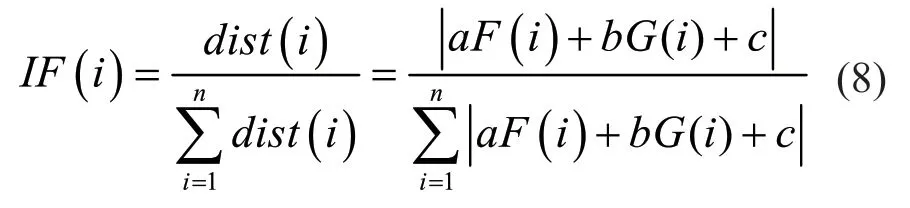
（3）T为预先设定的阈值，当IF(i)＞T时，将xi与yi视为误匹配，将其剔除；否则认为是正确匹配。

偏最小二乘方法具有计算简单、速度快的优点，但也存在一些不足：

（1）异常数据误差较大，会使函数模型偏离实际数据，影响检测精度[12]；

（2）误匹配点检测精度完全依赖于选择的函数模型，模型选择不准确影响检测结果。

2.2 基于统计模型的方法

基于统计模型的方法是统计满足给定条件的最多数量的匹配点。最常用的就是抽样随机一致性算法（RANSAC）。由Fischler M A等[13]于1981年最先提出，它是根据一组包含异常数据的样本数据集，计算出数据的数学模型参数得到有效样本数据的算法。RANSAC算法假定样本由正确数据与异常数据构成，可被模型描述的点称为“内点”，偏离模型的点称为“外点”。通过给定一组正确的数据，存在可以计算出符合这些数据的模型参数的方法。这里设定一个阈值t∈R，使得全部被判定为内点的点都不超过该阈值，RANSAC算法步骤如下：

（1）考虑一个最小抽样集的势为n的模型（n为初始化模型参数所需要的最小样本数）和一个样本集P，集合P的样本数Num(P)＞n，从P中随机抽取包含n个样本的P的子集S初始化模型M；

（2）余集CPS=PS中与模型M的误差小于设定的阈值t的样本集以及S本身构成S*。S*认为是模型M的内点集，它们构成S的一致集（Consensus Set）；

（3）若Num(S*)≥N（N表示正确模型所含一致集的最小个数）认为模型M是正确的，并利用S*（已经确定为内点集）重新计算得到新的模型M*，重新随机抽取新的S，重复以上过程。

（4）在完成一定的抽样次数后，若未找到一致集则算法失败，否则选取抽样后得到的最大一致集判断内外点，算法结束。

（5）上述过程经过一定次数的重复迭代执行，每一次生成的模型或者由于存在过少的一致集内的点而被拒绝，或者得出一个新模型对应着一个一致集。由于匹配过程中所需要的局内点的数目和迭代次数均未知，迭代次数k可以用如下公式估算：

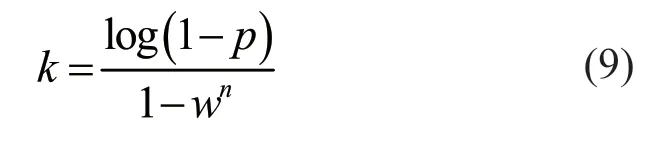
式中：n为估算模型参数所需要的最少数据点；p表示算法给出的结果是最优的概率，一般取值为0.99；w表示所有数据点中“内点”比例。在实际中，w是无法提前知道的，通常是在算法迭代中不断更新。也可以采用自适应的方法来初始化k和w。另外，距离阈值t也是一个重要的参数需要被初始化，在外点距离不知道的情况下，定义阈值参数只能依靠多次试验。

RANSAC算法具有算法简单，鲁棒性强等优点，在图像误匹配点检测中得到了广泛的应用[14-15]。但也存在一些不足：（1）迭代次数不确定，次数较少可能导致无法找到最佳模型参数，次数太多会导致计算速度降低；（2）针对多个模型，算法不适应。

3 侧扫声呐图像融合及其评价

3.1 图像融合

本文采用小波融合法实现相邻条带的侧扫图像融合。该方法能够在提高图像质量的同时，最大限度地保存各条带的原始信息，消除镶嵌过程中产生的拼接痕迹。小波融合法的基本原理是对原图像进行分解，生成所有高频和低频图像的组合图像，再对各个子图像多层分解得到次级子图像。再在变换域上进行特征选择创建融合图像，最后进行图像重构得到融合图像。通常分为以下4个步骤：

（1）对相邻条带声呐图像进行配准；

（2）对高、低分辨率的声呐图像进行n次小波变换，获得相应分辨率的低频轮廓图像和高频细节图像；

（3）用全色图像的高频部分来替代光谱图像的高频部分；

（4）对替换后图像进行小波逆变换，得到融合后的声呐图像。

3.2 图像融合效果评价

声呐图像融合效果可借助灰度均值、标准方差、熵、联合熵来进行评价。均值和标准方差反映图像的平均亮度和相对整幅图像的离散度；图像熵值反映了图像灰度值较整幅图像的平均灰度的离散情况；联合熵可以用来评价三幅图像之间的相关性，反映了两幅镶嵌图像和融合后图像之间的联合信息，联合熵值越大，表示融合后图像质量越好。

4 实验分析

4.1 误匹配点剔除算法实验分析

本文选取的实验数据为侧扫声呐采集的相邻条带影像，采用VS2010进行程序设计。通过两种算法对经过斜率和阈值约束后的特征点对中的一幅声呐图像特征点进行实验，特征点数量为149个，得到结果如图2所示。

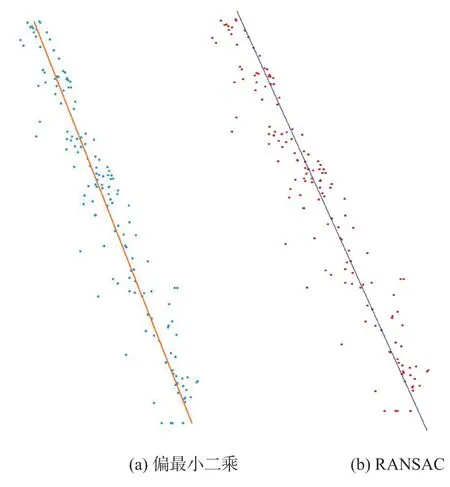
图2 误匹配点剔除效果图

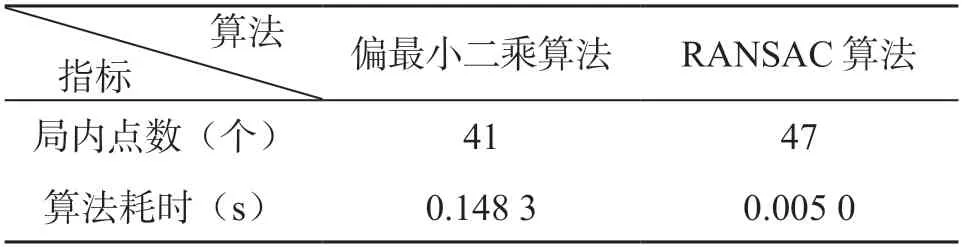
表1 两种算法的局内点数

根据表1可以发现，在相同约束条件下，RANSAC算法得到47个局内点，算法耗时0.005 s；偏最小二乘法得到41个局内点，算法耗时0.148 3 s。RANSAC算法对坐标点数据进行了多次迭代计算得到了最佳的模型，数据量较小，迭代次数并没有对RANSAC算法的计算速度造成实质性影响，计算耗时远小于偏最小二乘算法且得到的局内点大于偏最小二乘法，运算效率高；偏最小二乘法的拟合结果考虑了所有特征点的位置得出一条最佳直线，虽然这些特征点是已经经过剔除了大量误匹配点的特征点，但仍存在一些较大的异常数据点会使拟合的函数模型偏离实际数据，从而导致拟合的模型误差较大；对于已经利用斜率距离约束后得到的条带图像的匹配点对，正确的特征点对数量较多，但仍存在一些异常数据点容易使得偏最小二乘算法得到偏离实际的函数模型。综上，RANSAC算法提纯声呐图像的特征点对效果更佳。

4.2 镶嵌方法实验分析

在利用RANSAC算法对条带图像匹配点对进行精确提取后，采用SURF算法镶嵌原始声呐条带图像以及USM算法锐化处理后的声呐条带图像，最后采取小波融合对重叠区域进行融合。利用传统镶嵌办法（地理编码镶嵌）进行对比，得到如下实验结果，如图3至图5所示。

图3 地理编码镶嵌图

图4 SURF算法镶嵌图

图5 USM处理后的SURF算法镶嵌图

根据图3至图5的侧扫声呐镶嵌图像可以发现，3种方法均在一定程度上实现了条带与条带的拼接。但采取地理编码方法镶嵌的声呐图像处于不同条带的同一目标物未能较好的融合，出现较大错位现象，图像重叠区域灰度较深且整体灰度不均衡。采用SURF算法镶嵌的声呐目标物融合较好，无明显错位现象，图像重叠区域灰度也更加均衡。USM算法是一种图像锐化算法，能够起到补偿轮廓、突出边缘信息的作用。采用USM算法处理后的SURF算法镶嵌图的目标物特征更为明显，最大程度地保留了重叠区域的目标物特征。表2为融合图像质量评价结果。

表2 融合图像质量评价表

从表2可以发现，3种方法进行镶嵌后的声呐图像相较于单条带图像熵值均较大，说明镶嵌之后的声呐图像所包含的信息量有所增加；采用USM锐化处理后的SURF算法镶嵌图的标准方差、信息熵、联合熵均大于原始条带SURF算法镶嵌图；原始条带SURF算法镶嵌图的标准方差、信息熵、联合熵均大于地理编码镶嵌图。说明采用SURF算法进行声呐图像镶嵌相较于地理编码镶嵌能显著提高图像的信息量，采用USM算法对声呐图像进行锐化处理，能有效加强图像特征，提高图像信息量，且融合后质量更好。

5 结论

本文研究了一种基于SURF算法的侧扫声呐图像精确镶嵌方法。通过两种误匹配点剔除算法的实验分析比较，选取RANSAC算法进行侧扫声呐图像误匹配点剔除。同时，采用 USM算法对原始条带图像进行图像增强，能够进一步提升相邻条带特征点的匹配精度。再结合小波融合法进行图像镶嵌。实验结果表明，SURF算法解决了地理坐标镶嵌造成的目标错位问题，且对条带图像进行USM图像锐化能够有效增强图像特征进而提高图像匹配精度，实现了侧扫声呐图像的精确镶嵌。