基于序列轮廓线的多波束水体影像目标三维重建

陈建兵，刘洪霞,2*，李东辉，梅 赛，冯成凯，阳凡林,6

（1.山东科技大学 测绘与空间信息学院，山东 青岛 266590；2.山东科技大学 数学与系统科学学院，山东 青岛 266590；3.青岛环海海洋工程勘察设计院，山东 青岛 266061；4.中国地质调查局青岛海洋地质研究所，山东 青岛 266071；5.江苏海洋大学 海洋技术与测绘学院，江苏 连云港 222005；6.自然资源部海洋测绘重点实验室，山东 青岛 266590）

水体数据是多波束声呐采集的最原始的数据，包含了波束从换能器至海底完整的声学信息[1]，将其按一定方式成像处理可生成多视角的水体影像（Water Column Image，WCI）。水体影像广泛应用于探测鱼群分布、水下沉船、海底热液喷口、冷泉羽状流以及海洋内波等[2-5]物理目标物，在水下地形测量、海事搜救和打捞、军事及地质活动等方面具有极其重要的应用价值[1]。随着多波束水体影像在诸多领域的应用，相关学者对水体数据的精细化处理展开了进一步研究。Werf A[6]通过多种成图方式分析水体数据，并精确测量出水下沉船的最浅点，这种方式对操作人员的专业知识背景要求较高。Liu H等[7]提出一种水体影像自适应软阈值去噪方法，可有效提高影像信噪比，降低水体影像识别难度。然而，目前对水体目标的识别与分析通常在二维水体影像中进行，难以满足目标物三维成像的需求，因此一些学者开始将三维可视化技术应用到多波束水体数据的处理过程中。Urban P等[8]根据羽状流水体影像构建三维体素网格，通过体积反向散射强度转换来计算羽状流气体通量，极大地提高了羽状流定量分析的精度。李东辉等[9]对水体影像目标识别进行分析研究，提出一种目标物自动提取方法，并完整的提取出沉船采样点，为三维重建提供了点云数据获取方法。

三维重建技术可快速获取物体的数字化模型，从而实现基于现实的3D虚拟显示效果，在医学仿生、逆向工程、地矿建模、游戏影视等领域产生巨大应用价值。用于三维重建的数据形式通常有点云、序列影像、平行轮廓线，此三种数据皆可由水体数据进行相应的处理得到，然而关于水体数据三维重建的相关文献资料却鲜有公开发表，一方面由于多波束声呐采集的目标点云空间分布具有严重的断层性、复杂性和非均匀性，直接利用点云重建目标物效果不佳；另一方面，水体影像中包含有未改正的载体姿态、吃水、声速剖面等方面的误差，根据序列影像重建易导致目标物变形扭曲。近些年，随着逆向工程行业的迅速发展，基于断层数据（如医学上CT、MRI扫描数据）的三维重建方法逐渐成为研究热点，轮廓线法是一种利用空间断层数据重建的经典方法，由Keppel E[10]在1975年提出，后来的研究者在轮廓线法基础上改进了约束条件的判断形式，形成最大体积法、最小表面法、最短对角线法、同步前进法和切开缝合法等[10-14]，这些方法在医学、地质等行业类似问题中展现出良好的适用性。

本文提出一种基于序列轮廓线的多波束水体目标物三维重建算法，通过点云分割对多波束单Ping（一个发射接收周期）数据做进一步细分处理并提取轮廓，在提取的序列轮廓线基础上，提出一种空间格网划分方法，通过局部优化算法建立顶点间拓扑关系，对空间格网形成面片填充，从而实现按“点—线—面”的顺序逐步重建水体目标。

1 多波束水体目标成像特征

多波束声呐通过连续接收每条波束的回波信号，可在声照射扇区内形成高密度采样，从而绘制水体影像。波束携带的能量会穿透整个水体到达海底，但声波在水下传播速度远比不上光速，声信号旅行时不可忽略，换能器连续发射声波的时间须限制在此前发射的声信号全部返回之后，因此水体数据是多波束声呐在航线上对水体的间断式扫描的结果。均匀、密集、稳定性好的采样数据是最理想的三维重建数据，而水体数据空间分布特征会对三维重建算法产生一定的影响。

1.1 水体目标成像机理

多波束声呐在工作时，以换能器基阵为中心，在一个平面内同时形成数百甚至上千条声学波束，这些波束携带的能量从换能器发射后，经水体传播至海底，波束在水下的传播过程中（包括水体、海底以及其它物体）会产生声散射现象，这些后向散射信号再由接收换能器接收并记录在水体数据中，从而完成水体数据一Ping观测。换能器发射基元会持续发射声波，伴随载体的移动，可得到一个类似三棱柱形状的水体扫描区域（图1-a）。

垂向扇形图与航向堆叠图是多波束水体影像最常见的两种形式。垂向扇形图以Ping为单位进行绘制，水体回波信号以极坐标的形式存储在水体数据文件中，计算采样点像素坐标，并将强度区间转换为灰度区间，即可得到一幅垂向扇形图（图1-b）。航向堆叠图可整体上观察水体情况，将一Ping水体数据按反向散射强度堆叠为一列，对当前测线所有Ping进行堆叠显示即可获得航向堆叠图（图1-c），图1-c中蓝线标识位置为图1-b堆叠结果。

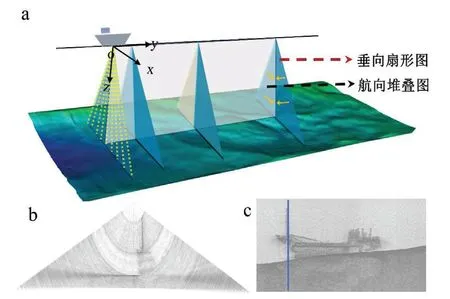
图1 多波束水体目标成图原理

1.2 水体数据空间分布特征

在不改变多波束声呐采样率的前提下，水体采样点在每个波束空间上均匀分布。由于波束在声照射扇面内是以换能器为中心，按固定的角度接收各个方向的声信号，因此越靠近换能器采样点越集中，随着水深的增加波束之间的几何缝隙逐渐扩大（图2-a），在一Ping水体影像中，边缘波束海底附近的采样点最为稀疏。在三维空间中水体数据的复杂性进一步扩大，通常水体数据在Ping平面内采样率高于航线方向，相邻Ping之间的空白区域较大，整体上呈断层式分布，另外由于载体姿态、吃水以及声速剖面等诸多不可控因素的影响，多波束沿航线采集的多Ping水体影像之间并非完全平行分布（图2-b）。因此多波束水体数据在空间中表现出严重的断层性、复杂性与非均匀性，对三维重建算法造成不利影响。

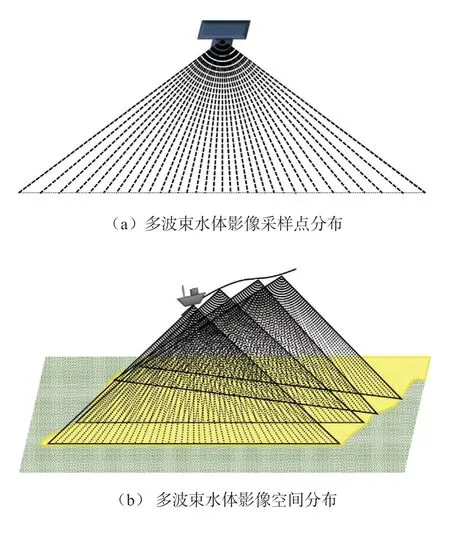
图2 多波束水体影像数据分布示意图

2 目标序列轮廓线三维重建算法

多波束声呐获取的水体数据空间分布情况较复杂，易导致算法重建失败，为提高水体目标三维模型的质量，本文基于最短对角线法局部优化准则，通过Ping内轮廓提取与Ping间面片填充实现按照“点—线—面”的顺序逐步分析处理数据，完成水体目标重建。首先根据点云数据生成目标整体的序列轮廓线，Ping是水体数据的基本组织单位，在Ping的基础上对点云做进一步细分处理并提取轮廓线，以避免轮廓线失真；在轮廓线面片填充时，由于相邻Ping轮廓线数量一致性难以保证，可能会出现多条轮廓线都与同一条轮廓线进行面片填充，即“分支”问题，这种情况可通过拆分轮廓线转换成多个一一对应的轮廓线填充形式，再使用轮廓线中心平移与划分空间格网的方法，完成“一对一”的轮廓线面片填充，最终形成目标物表面模型。

2.1 最短对角线法原理

轮廓线法是以一系列大致平行的轮廓线作为建模数据，相邻轮廓线之间以一系列细小的三角形面片填充，从而生成整个表面模型。在生成三角形面片的过程中，需要不断进行判断与调整，使得模型整体匀称、视觉效果好。最短对角线法作为一种局部优化准则，具有计算量小、构网均匀、简便快速的优点，应用广泛。该算法原理如图3所示，假设多波束相邻两Ping的轮廓线分别为P和Q，在四边形pipi+1qi+1qi中，两对角线长度分别为r1和r2，若r1＜r2，则将三角形piqiqi+1加入三角网，否则，将三角形pipi+1qi加入三角网，同时，四边形前进构建下一个三角形，逐步扩展三角网直到重新返回起点。

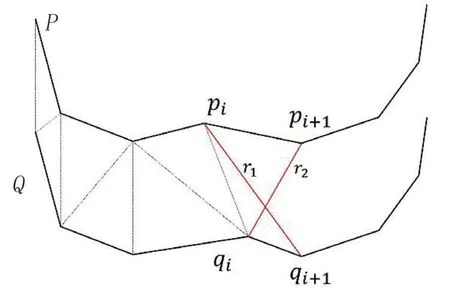
图3 最短对角线法示意图

2.2 多波束Ping内点云轮廓提取

多波束水体数据是按Ping进行采集、存储和处理的，但在提取水下目标序列轮廓线时，以Ping为单位提取可能会导致轮廓线失真，因为每Ping代表水体的一个断面测量，考虑到复杂结构的水下目标的情况，一Ping数据中可能同时包含一个物体多个子结构的剖面（如图4-a中水下沉船的缆绳与船身），对多个不连续的剖面生成同一条轮廓线，会降低轮廓线的精度，因此需在轮廓线提取之前对Ping内点云进行分割。本文根据点云之间的欧式距离进行聚类，将距离较近的点划分为一类，然后再以类为单位提取轮廓（图4-b）。依次处理所有Ping点云从而获得整个目标物的序列轮廓线。

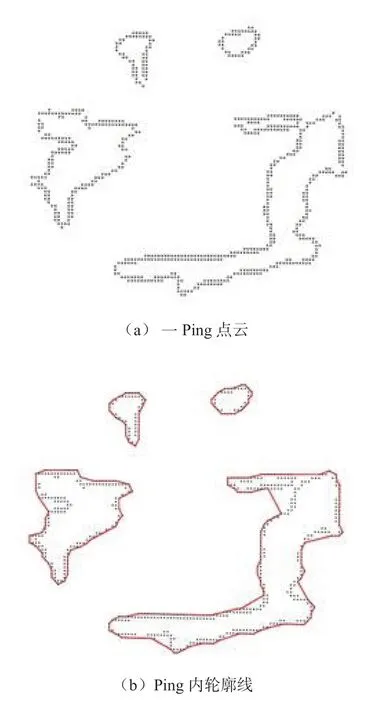
图4 Ping内轮廓线生成

2.3 多波束相邻Ping间填充

相邻Ping轮廓线对应关系分为“分支”和“一对一”两种形式，而“分支”问题会导致模型面片交叉、数据冗余，难以控制模型的质量，需对“分支”问题进行合理转化，使面片填充统一在“一对一”的形式下进行。

2.3.1 相邻Ping间“分支”问题“分支”问题是由于水下目标在航线方向的几何结构发生变化所导致的轮廓线数量不一致，合理解决“分支”问题是检验算法有效性的关键。目前现有文献提供的解决方案主要有两种，一是利用插值算法在分支轮廓线与母轮廓线之间添加过渡轮廓线[15-16]；二是创造辅助线将母轮廓线分割成几块，然后再对分割出来的轮廓线进行填充[17-18]。对于多波束水体数据，由于数据量较大，添加过渡轮廓线将进一步增加计算量，降低算法效率，且插值算法的精度不易验证；创造辅助线切分凹轮廓线时，切分结果与“分支”轮廓个数可能出现差异，且分支数目越多，处理起来越困难。本文通过在母轮廓线上添加断点对轮廓线进行拆分，将“分支”问题转化为多个“一对一”填充，优点是以点拆分轮廓线比辅助线分割更灵活，且不会增加额外的数据量。

图5中第iPing的两条轮廓线都与第i+1 Ping轮廓线形成填充关系，通过插入两个断点可将第i+1 Ping轮廓线拆成两条完整的轮廓线，从而将“二对一”填充问题转换成两个“一对一”填充。为使得轮廓线拆分合理、视觉效果更好，在第i+1 Ping轮廓线上，按照最小距离差的方法插入断点，具体方法如下：遍历第i+1 Ping轮廓线上所有的点，分别计算到第iPing两条轮廓线的最短距离r1和r2，在|r1-r2|达到最小处插入断点，利用这些断点将母轮廓线拆分成两段。然后再分别计算拆分的两条轮廓线中心点与第iPing中两条轮廓线中心点的距离，对这两Ping轮廓线进行匹配，形成两个“一对一”的填充关系。

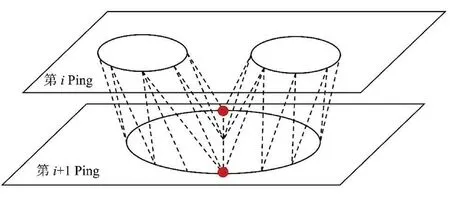
图5 拆分轮廓线

2.3.2 “一对一”填充 对于相似性较好的轮廓线，可以直接以最短对角线法作为约束准则进行填充。但是，当两轮廓线的位置和形状差异过大时，可能会出现图6中的错误，从而使算法失效。

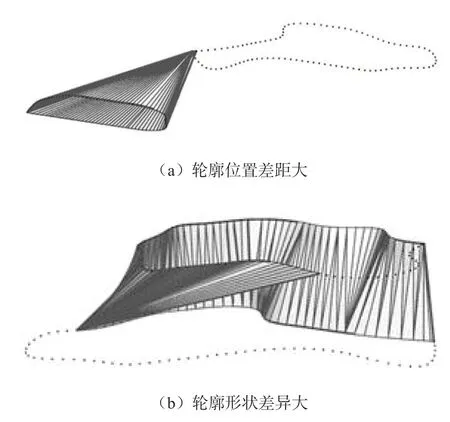
图6 最短对角线法失效的两种情况

轮廓线错位易导致图6-a中的圆锥面，需在面片填充之前进行轮廓线中心平移，使两轮廓线的中心在Ping平面法线方向重合，然后按最短对角线法进行面片填充（图7-b），最后再将点云的拓扑关系映射回平移之前的轮廓线上（图7-c）。

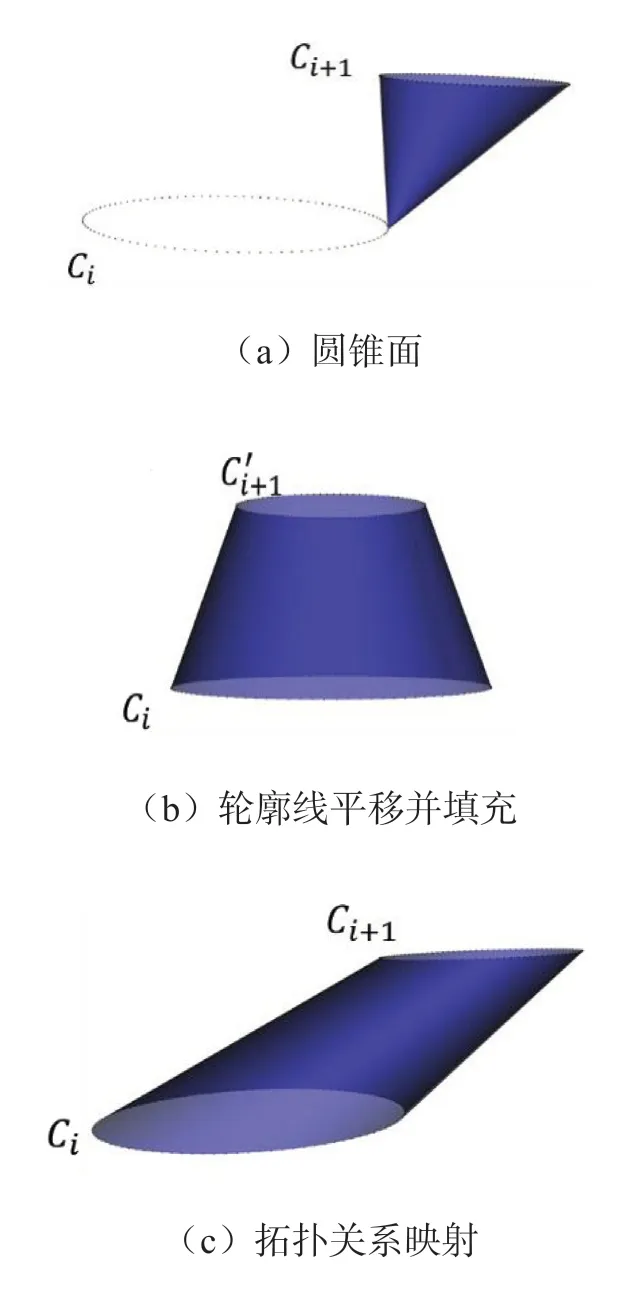
图7 轮廓中心平移示意图

图6-b中的错误是由于上下轮廓线相似性不好，且拐点较多，最短对角线法在拐点出现的轮廓线上容易出错，在两条轮廓线上不能同步前进，算法继续进行则出现图8-a中的面片自相交情况。在拐点较多的轮廓线上生成面片时，先在轮廓线之间划分出一系列空间格网，如图8-b所示，对每一块空间格网可以看作是一个上下边为曲线的空间四边形，把复杂轮廓线的填充转化为对每一个空间四边形的填充，这些空间四边形上下边的曲率变化相对简单，即使出现图6-b中不同步构网的情况，也能将其限制在该格网内，避免继续传播影响相邻的格网。

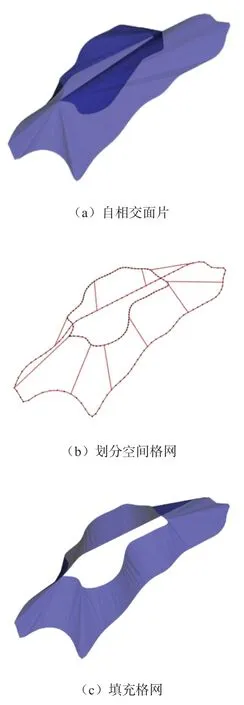
图8 划分空间格网示意图

划分格网的具体方法：在下层的轮廓线中均匀插入n个点P={pi|i∈[1,n]}，将该轮廓线等分成n份，在上层轮廓线上插入n个点Q={qi|i∈[1,n]}，且qi是上层轮廓线上与pi距离最近的点，连接这n对断点便在两轮廓线间形成n个空间格网，如图8-b，最后再采用最短对角线法在每一个格网上生成三角形面片，从而在两轮廓线之间形成完整表面，如图8-c。

综上所述，首先对多波束水体点云数据提取序列轮廓线，然后按航向顺序在相邻Ping轮廓线之间填充面片，从而形成水体目标表面模型，最后通过模型渲染提升视觉效果。具体流程如图9所示。

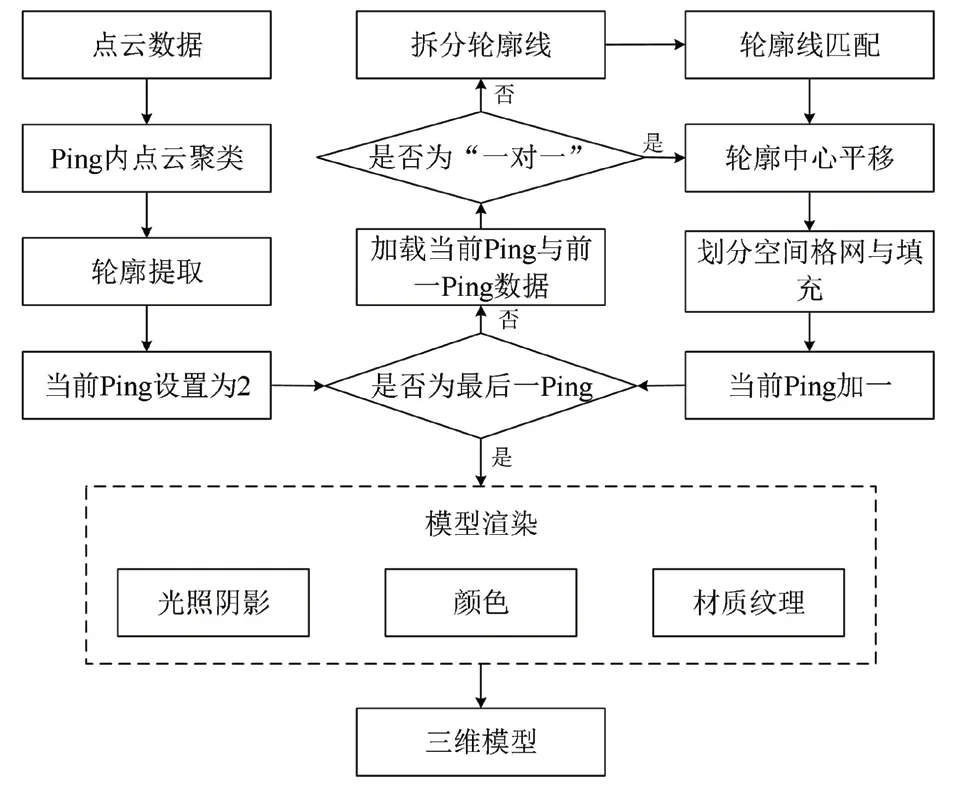
图9 算法流程

3 实验与分析

本次实验采用Kongsberg公司提供的实测数据。数据采集地点为加拿大悉尼市玛格丽特公主海滨公园附近海域（48°43.323'N，123°21.339' W），使用Kongsberg EM3002型多波束声呐系统对G.B.Church号水下沉船进行扫描，此船全长53 m，宽11 m，沉没于平坦砂质海底（图10），周围水深24～27 m。数据采集时，多波束声呐采样率设置为7 146.5 Hz，波束数和波束开角分别为160°和130°，表层声速为1 477 m/s，船体横跨145Ping数据。沉船形状复杂、细节保留丰富，具有较高的代表性。

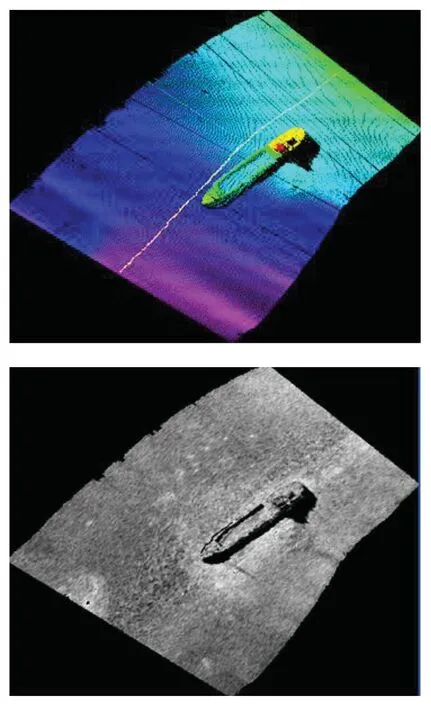
图10 多波束水深图和海底反向散射强度图像

通过解析多波束水体数据并绘制成图，可得到多视角下的水体影像（图11），采用李东辉等[9]介绍的水体影像目标自动提取算法从原始水体数据中提取沉船点云，逐Ping对采样点进行聚类分割，含有沉船的145Ping数据被细分为416类，从而提取出416条轮廓线，沉船整体的序列轮廓线如图11左下图所示。

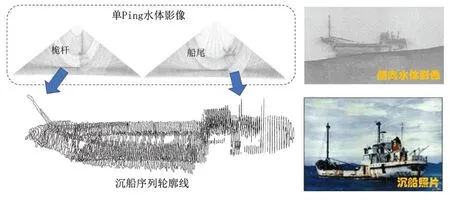
图11 沉船水体影像及序列轮廓线

根据图11中的序列轮廓线，分别采用最短对角线法和本文算法进行重建，结果如图12所示，直接使用最短对角线法所建的模型中，圆锥面和自相交面片情况导致模型中出现多处不合理结构，如桅杆和船尾部位，这体现了传统轮廓线算法对于复杂轮廓线处理的局限性。本文算法针对模型中大量出现的圆锥面和自相交面片进行改进，在可控的小范围内生成首尾相连的三角网，降低了处理复杂轮廓线的难度，同时，模型结构得到改善，形状更加合理。本文算法在Visual studio 2013平台上使用C++语言实现，并借助VTK（Visualization Toolkit）对结果进行可视化。

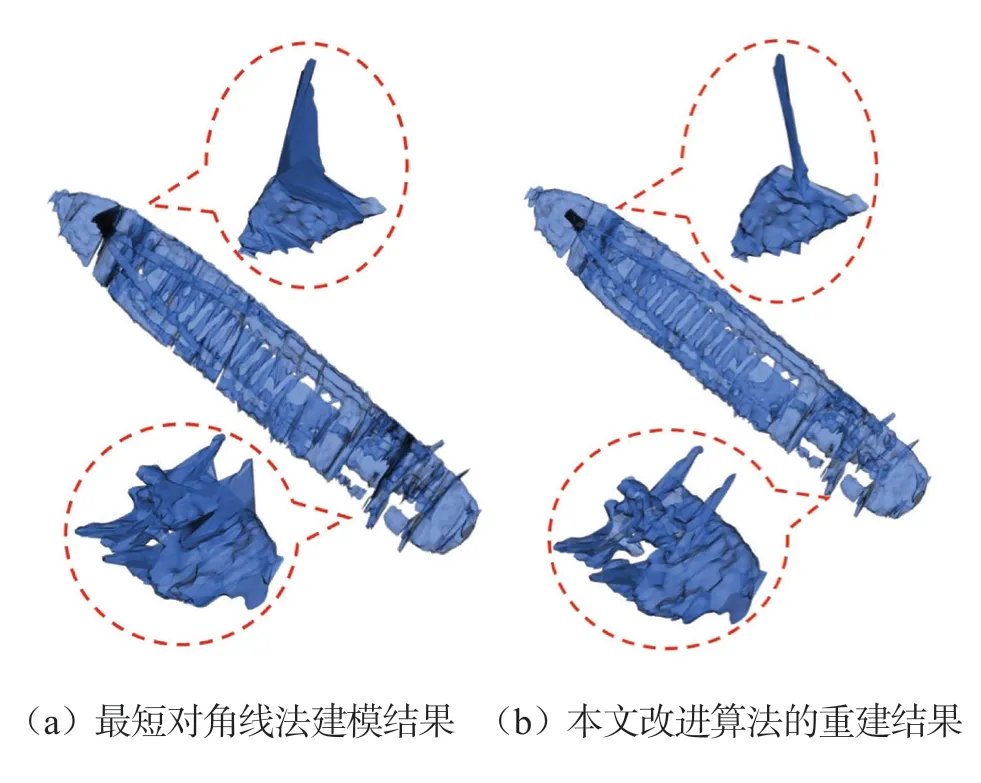
图12 轮廓线算法建模结果对比图

为进一步验证本文算法对水体数据的适用性，使用α-shape[19]算法与抛雪球算法[20]对沉船点云进行重建。α-shape算法与抛雪球算法是经典的三维重建算法，其中α-shape算法是在Delaunay三角剖分基础上，根据指定的α值选取剖分结果中的α簇作为表面模型；抛雪球法需要将输入的点云数据转换成体数据，按照分布函数计算每个体素对投影平面像素点的贡献值，从而实现点云数据的三维重建。对上述两种算法进行多次试验以挑选最佳参数值，图13和表1展示上述两种算法与本文算法重建效果及统计结果。

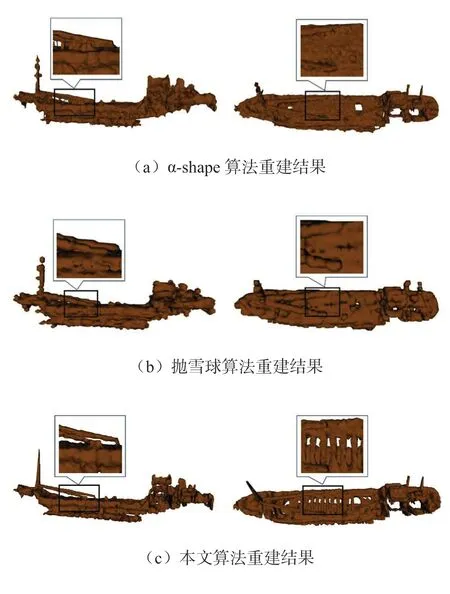
图13 不同算法重建结果对比

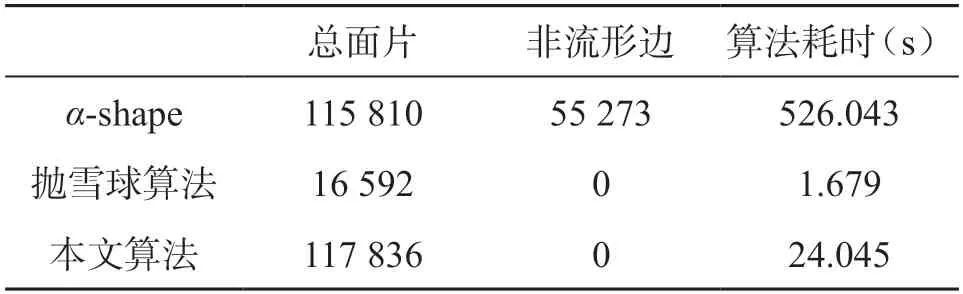
表1 不同算法重建结果统计表

从图11的沉船照片中可以看到，桅杆尺寸较小，水体数据在此位置采样点稀疏，α-shape算法将桅杆还原成螺旋形状，而抛雪球算法重建结果中，桅杆粗糙不平，有明显凸起。在缆绳与船身连接位置，由于二者距离较近，α-shape算法与抛雪球算法均将缆绳与船身连为一体。在船舱位置有一排狭长开口，开口排列方向大致与Ping平面方向垂直，这些开口在α-shape算法与抛雪球算法的重建结果中均没有体现。从图13的3种算法的对比中可看出，本文算法更符合目标物形状，对桅杆、缆绳、船舱开口等细节还原准确，模型中的面片大小均匀，整体视觉效果较好。对三种模型的数据量和运行时间进行统计，从表1中可以看出α-shape总面片和非流形边数量最多，非流形边是3个或以上面片的交线，非流形边大量出现表明模型存在面片交叉问题；而抛雪球算法面片数量和运行时间最少，但模型特征还原不够精准，表面结构冗余。

另外，考虑到多波束系统在连续工作的过程中，受海况或系统自身问题影响，时有出现某Ping水深和水体数据异常，这些异常数据不符合目标形状，可事先检查异常Ping并剔除，在剔除异常Ping之后水体数据整体仍为断层式分布。本文算法针对空间断层数据进行组织与优化，算法的正确运行不依赖于数据的空间密度和分布均匀性，具有较强的鲁棒性，本文算法对剔除异常Ping之后的数据仍然有效。因此，本文算法对多波束水体数据三维重建是合理且实用的。

4 结论

三维重建技术可解决多波束水体影像对目标成像不够全面、直观的弊端，本文充分考虑数据的断层性、复杂性与非均匀性对重建算法的影响，基于传统轮廓线法建模原理，提出了按“点—线—面”顺序对水体目标逐步重建的方法，针对几何结构复杂的目标，先进行Ping内点云聚类再提取轮廓线，可生成与真实情况契合度较好的轮廓，并通过轮廓线拆分、轮廓中心平移与划分空间格网的步骤能有效解决复杂轮廓线间面片填充的问题，避免面片交叉、连接错误的现象。实验证明该算法稳健性强，模型准确度高，相比于传统轮廓线算法以及目前常用的点云三维重建方法，本文算法整体上无错误结构，且对小尺度上的细节特征也有精准还原，在处理复杂的水体目标物时展现了良好的适用性，可在水下目标精准识别与定量分析工作中产生较大的实用价值。