灰色预测模型在公路交通量预测中的应用

段莹超

(黄河勘测规划设计研究院有限公司，河南 郑州 450003)

交通量可直观反映公路建设项目的等级及规模，交通量预测的水平和质量将直接影响到公路建设项目决策的科学性，因此为避免和减少项目前期工作带来的损失和浪费，交通量需求预测工作成为公路建设项目可行性研究的重要环节。目前，公路项目的交通量需求预测方法较多，根据《公路建设项目可行性研究报告编制办法》的要求，公路建设项目的交通量预测一般采用“四阶段预测法”，同时说明了对二级及以下公路建设项目可采用其他预测技术。

1 灰色预测模型

1.1 灰色系统理论

灰色系统理论由我国著名学者邓聚龙教授提出，它的研究对象是“部分信息已知，部分信息未知”的“小样本、贫信息”不确定性系统。灰色系统理论对各项观测、试验数据没有特别的要求和限制，且需要的研究样本少、适用范围广，因此灰色系统理论自提出后，各个领域的技术人员对其进行了广泛的研究，并取得了丰硕的应用成果。灰色系统理论主要包括为以灰色代数系统、灰色方程、灰色矩阵等为基础的理论体系；以灰色关联空间为依托的分析体系；以灰色序列生成为基础的方法体系；以灰色模型为核心的模型体系；以系统分析、评估、建摸、预测、决策、控制、优化为主体的技术体系。

1.2 与交通量预测的适应性

道路交通系统是一个存在多因素影响、多层次结构、多目标体系的复杂系统。公路建设项目交通量预测普遍采用的“四阶段预测法”就是通过揭示交通量与各影响因素之间的关系，达到预测未来交通流变化趋势的目的。为了准确描述未来交通源、交通目的地、交通流路径等信息，就必须弄清楚过去的社会、经济、人口、政策等因素，并预测这些因素在未来一定时期的变化情况。但在我国，由于对公路交通需求预测的研究开展较晚，在基础资料记录、收集及整理方面存在严重不足，特别是对等级相对较低的公路，各种基础数据存在短缺、误差甚至是作假的现象，能收集到的反映交通量动态特征的数据较少。基础数据的欠缺造成交通流系统的状态、结构、内在特征难以被描述，各种影响因素的作用机制难以明确，而这样的系统便属于典型的灰色系统。

灰色理论可以利用存在的较少的或不确切的表征系统行为特征的基础数据构造原始数据序列，作生成变换后建立微分方程，该灰色过程建立的模型称为灰色模型，简称GM模型。灰色预测模型可以根据已知的历史小样本、不确定的信息，建立一个从过去延伸至未来的GM模型。对于交通量预测而言，灰色预测模型可以抛开社会、经济等影响因素，利用历史交通流数据，寻求建立交通量与时间推移变化的关系，达到预测交通量的目的。

1.3 模型的建立

灰色预测模型就是利用离散的数据序列建立灰色的微分方程模型，累加生成运算是整个模型建立的基础。x(0)(t)为收集到的过去或现在的系统数据，在数据不完整，信息量不足的情况下，用统计学的方法寻找数据规律是不可行的，但对数据进行一定程度的规律性强化是可能的，其强化途径就是进行累加生成运算得到新的时间数据序列x(1)(t)。新生成的数据序列相对于原始数据序列而言，其不确定性明显被弱化，规律性明显增强，由此求解得到生成函数并建立系统数据可利用的灰色预测模型。模型建立的详细步骤如下：

(1)构造原始数据序列x(0)(t)。

x(0)(t)={x(0)(1)，x(0)(2)，…，x(0)(n)}

(1)

(2)利用生成运算，构造累加数据数列。

(2)

x(1)(t)={x(1)(1)，x(1)(2)，…，x(1)(n)}

(3)

(3)利用序列x(0)(t)、x(1)(t)构造数据矩阵B、yn。

(4)

yn=[x(0)(2)，x(0)(3)，…，x(0)(n)]T

(5)

(4)求解特征向量a、u。

(6)

(5)将特征向量带入时间响应函数。

(7)

(6)对式(7)求导可得到灰色预测模型。

(8)

(7)计算模型精度检验参数。

(9)

相对误差：e(t)=(q(0)(t)/(x(0)(t)

(10)

(11)

(12)

(13)

(14)

(8)利用后验差检验法对模型进行精度检验。

根据C值与P值的大小，将预测精度分为四个等级，各等级标准见表1。

(9)若检验预测精度达不到要求，可建立残差GM(1，1)模型进行修正。

(10)交通量预测分析。

表1 预测精度等级

2 项目应用

2.1 项目概况

项目位于陕西省渭南市，为缓解G108国道某段主线交通压力，在该段主线东测计划修建复线工程，规划道路路线长37.7 km。通过搜集项目区域内社会经济相关历史数据发现，该段国道的历史交通量数据较少，区域内经济发展数据欠缺且呈离散性，为保证交通量预测的准确性，项目利用灰色预测模型进行交通量预测。该段国道2011～2018年历史交通量见表2。

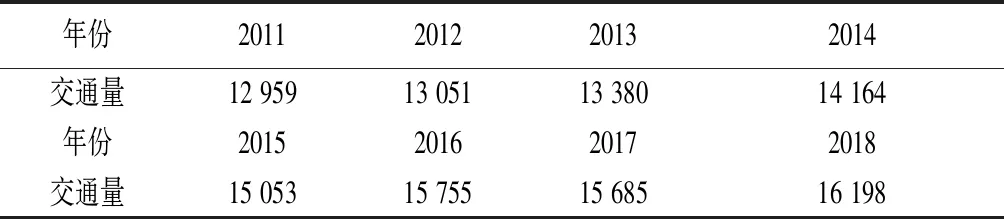
表2 G108国道某段历史交通量( pcu/d)

2.2 项目交通量预测

(1)构造原始数据序列并进行一次累加变换，得到累加数据序列。

x(0)(t)={12 959，13 051，13 380，14 164，15 053，15 755，15 685，16 198}

x(1)(t)={12 959，26 010，39 390，53 554，68 607，84 362，100 047，116 245}

(2)利用原始数据序列及累加数据序列构造数据矩阵B，yn。

yn=[13 051，13 380，14 164，15 053，15 755，15 685，16 198]T

(3)计算特征向量a、u。

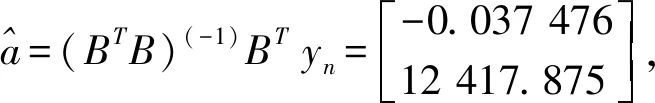
(4)将特征向量带入时间响应函数并求导得到灰色预测模型。

(15)

(5)利用历史数据对模型进行后验差检验，计算残差、相对误差、后验差比值及小误差频率，结果见表3及表4。

(6)由表1可知模型预测精度为好，预测模型可以在项目中应用。

(7)利用灰色预测模型预测国道特征年趋势交通量见表5。

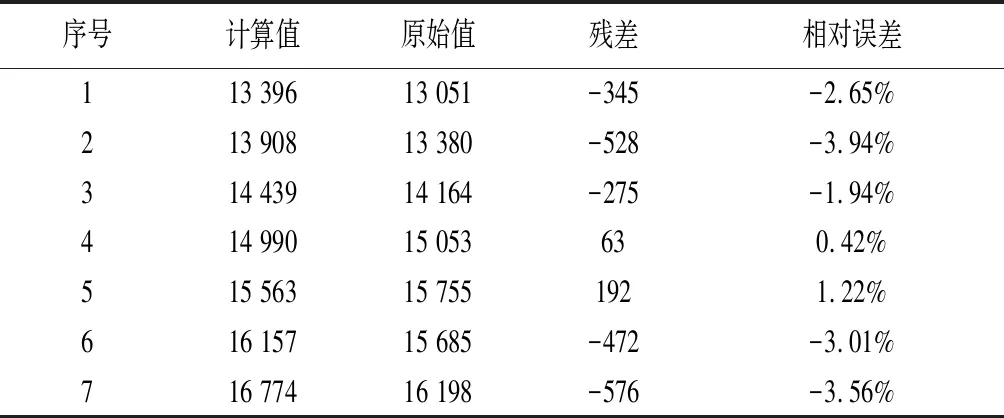
表3 残差、相对误差结果

表4 后验差比值及小误差频率结果

表5 G108国道某段趋势交通量( pcu/d)

(8)利用容量限制的最短路径分配法对项目进行交通量分配预测，得到项目趋势交通量。

(9)项目的建设会在影响区内产生一定的诱增交通量。根据诱增交通量的特性，通过对部分已经通车产生效益的公路进行的后评估研究，诱增交通量可以采用特定的数学模型进行计算。参考相关研究成果，结合项目自身特点，构造诱增模型如下：

y=1 740/(1+2.137-0.2201x)

(16)

式中：y-交通量预测值；x-项目通车后年份。

(10)受项目区域交通形式分布限制，项目无转移交通量。则项目预测交通量为趋势交通量与诱增交通量之和，预测结果见表6。

表6 项目预测交通量( pcu/d)

4 结 语

对于二级及以下等级的公路建设项目，由于各种基础资料普遍缺乏，按照一般的“四阶段预测法”难以准确地预测其远期交通量。灰色系统理论是一种能够从较少的数据和信息中找到系统内在规律的方法，将灰色预测模型应用于较低等级公路交通量预测中，可以通过有限的数据将交通量和时间关联，从而预测出远期交通量，准确性较高，具有良好的适用性。