基于小波变换的负荷谐波概率密度函数分析
2020-03-17杨宏伟郭立杰
杨宏伟,郭立杰
(1.国网北京通州供电公司,北京101101;2.国网北京昌平供电公司,北京102200)
0 引 言
谐波阻抗作为电能质量分析的重要技术指标,在电能质量限制值计算中起着重要的作用,而谐波限制值的计算又直接影响到用户的谐波运行水平。因此,如何方便快捷而又准确地计算谐波阻抗,对于电能质量行业的发展有着重要影响。现有的谐波阻抗多是使用仪器记录电压和电流瞬时值波形,然后根据信号处理方法得到谐波阻抗。这种方法具有原理准确的特点,但对电力系统的监测水平提出很高要求,需要最大的经济投入,且这种方法无法满足较长监测周期内的谐波阻抗变化趋势,无法完全满足电能质量监测和治理的需要。
为弥补上述方法的缺陷,国内专家提出一系列方法对上述方法进行改进。文献[1]提出正交多项式和统计量来应用于矢量求和的概率密度函数,为应用统计方法解决电能质量问题提供了理论基础。文献[2-3]针对实际电铁电能质量谐波进行概率分析研究,为后续非线性负荷研究提供了可供借鉴的模型。文献[4-6]应用一类正交多项式对谐波求解问题进行分析,为研究实际中多谐波源之间的关系提供了有力工具和方法。上述方法多是基于瞬时值已知的前提计算谐波阻抗,但实际电能质量监测过程中,都是以有效值形式储存于数据库中,瞬时值虽然信息量完整,但需要存储空间巨大,只有在极少数场合才得到应用。而电力系统模型都是基于瞬时值建立的,以上文献并未考虑有效值和瞬时值之间的概率关系。已知有效值的概率密度函数,反求瞬时值的概率密度关系属于谐波求和的逆问题。
笔者在前人研究成果的基础上,首先选取实际测量中的3 s有效值,并拟合出3 s有效值的概率密度分布,并根据3 s有效值和200 ms值关系,得出200 ms的概率分布。在仿真中验证了小波变换在概率密度函数计算过程中的有效性。
1 小波变换
电能质量测试中电流和电压值是以有效值的形式展现的,下面阐述各种有效值的定义。
1.1 小波变换
小波变换作为一种具有良好的局部化刻画信号处理方法,通过构造与信号相似的小波基函数,以及对基函数的伸缩和平移来实现灵活刻画信号的目的,小波变换从原理来讲也是一种信号的正交分解。一种常见的小波变换表达式如下:
(1)
式中:cA1(x)为近似系数向量,cDi(x)为细节系数向量。
1.2 Gram-Schmidt正交化
式(1)得到的近似系数向量和细节系数向量如果没有正交的话,可以通过Gram-Schmidt正交化过程实现正交,对应的步骤如下:
p0(x)=cDn
(2)
(3)
(4)
(5)
当多项式和区间[a,b]确定之后,正交化多项式也是唯一的。f(x)对应可以写为区间[a,b]上的正交多项式的线性组合。
2 3 s有效值和200 ms有效值定义
2.1 200 ms值
对瞬时信号做傅里叶变换,即可得到n次谐波的幅值和相角。电能质量计算中约定每200 ms得到一组有效值,即200 ms值。文献[7-8]定义50 Hz系统谐波的计算值计算周期为10个周期,即200 ms得到一组谐波值。对应的表达式如下:
(6)
式中:w为频率,abs为求解幅值函数,urms_1s(w)为w频率对应幅值。
2.2 3 s有效值
对3 s内上述15个“连续200 ms有效值”作均方根计算。
(7)
式中:urms_1s为3s有效值,N=15。
式(7)定义式是在式(6)基础上得出的。为了处理方便,对式(7)做出如下变形:
(8)
3 3 s有效值和200 ms值概率密度函数统计量的关系
根据式(8)的关系和概率统计中均值和方差性质,可以得出200 ms值平方的均值和方差为
u200ms=u2s
(9)
σ200ms=15σ3s
(10)
式中:u200ms为200 ms值平方的均值,σ200ms为200 ms值平方的方差。
4 概率密度函数计算
4.1 3 s有效值平方概率密度函数计算
3 s有效值平方的概率密度函数可以通过实测的3 s电能质量数据拟合得到,3 s有效值平方的均值和方差也可以通过3 s有效值平方统计得到。假设3 s有效值平方均值为μ3s,方差为σ3s。
4.2 200 ms值概率密度函数计算
假设200 ms值平方的概率密度函数为f200ms-2(x),在定义区间上进行小波正交展开:
(11)
式中:ai为正交多项式的系数,对应的表达式为
ai=〈pi(x),f200ms-2(x)〉
(12)
其中:〈pi(x),f200ms-2(x)〉为pi(x)和f200ms-2(x)的内积,也为变量x函数pi(x)的期望。对式(12)进行泰勒级数展开,保留前三项,可得
(13)
对于没有表达式的pi(x),用微分跟踪器求取其二阶微分。
5 微分跟踪器
微分跟踪器是为了求取含有噪声数值信号的微分信号而设计的,具体的表达式详见文献[9]。
6 仿真分析
为了验证理论的有效性,提取FLUKE1760仪器对现场谐波测试数据。选取电力系统电力机车、整流站2种典型负荷进行计算分析。小波分解采用bior3.5基函数,分解层数为4层,小波基和层数是根据电能质量数据而定的,没有量化的判断标准。
6.1 牵引站电流数据分析
牵引站电流3 s有效值平方的拟合曲线和小波分解如图1、图2所示。根据图2得到牵引站3 s电流有效值平方分解系数之后,根据式(2)~(5)得到正交向量,再根据式(12)得到200 ms电流有效值概率密度函数的系数。具体的图形如图3所示。

图1 牵引站电流3 s有效值平方的拟合曲线Fig.1 Fitting curve for 3 s RMS square of current in traction station

图2 电流3 s有效值平方的小波分解Fig.2 Wavelet decomposition for 3 s RMS square of current

图3 电流200 ms有效值平方的概率密度Fig.3 Probability density for 200 ms RMS square of current
从图3可以看出,200 ms电流有效值继承了图2小波分解中近似系数cA1的主要部分,细节系数分量cD1也有所体现,但相比较图1的3 s有效值曲线,已经有所减小。
6.2 换流站电能质量数据分析
图4为换流站电流有效值平方的拟合曲线,对其进行小波分解,分解层数为9层,小波基函数为dmey,分解之后的高频和低频分量如图5所示。截取cA1、cD8、CD9为有效分量。

图4 换流站电流3 s有效值平方的拟合曲线Fig.4 Fitting curve for 3 s RMS square of current in convertor station
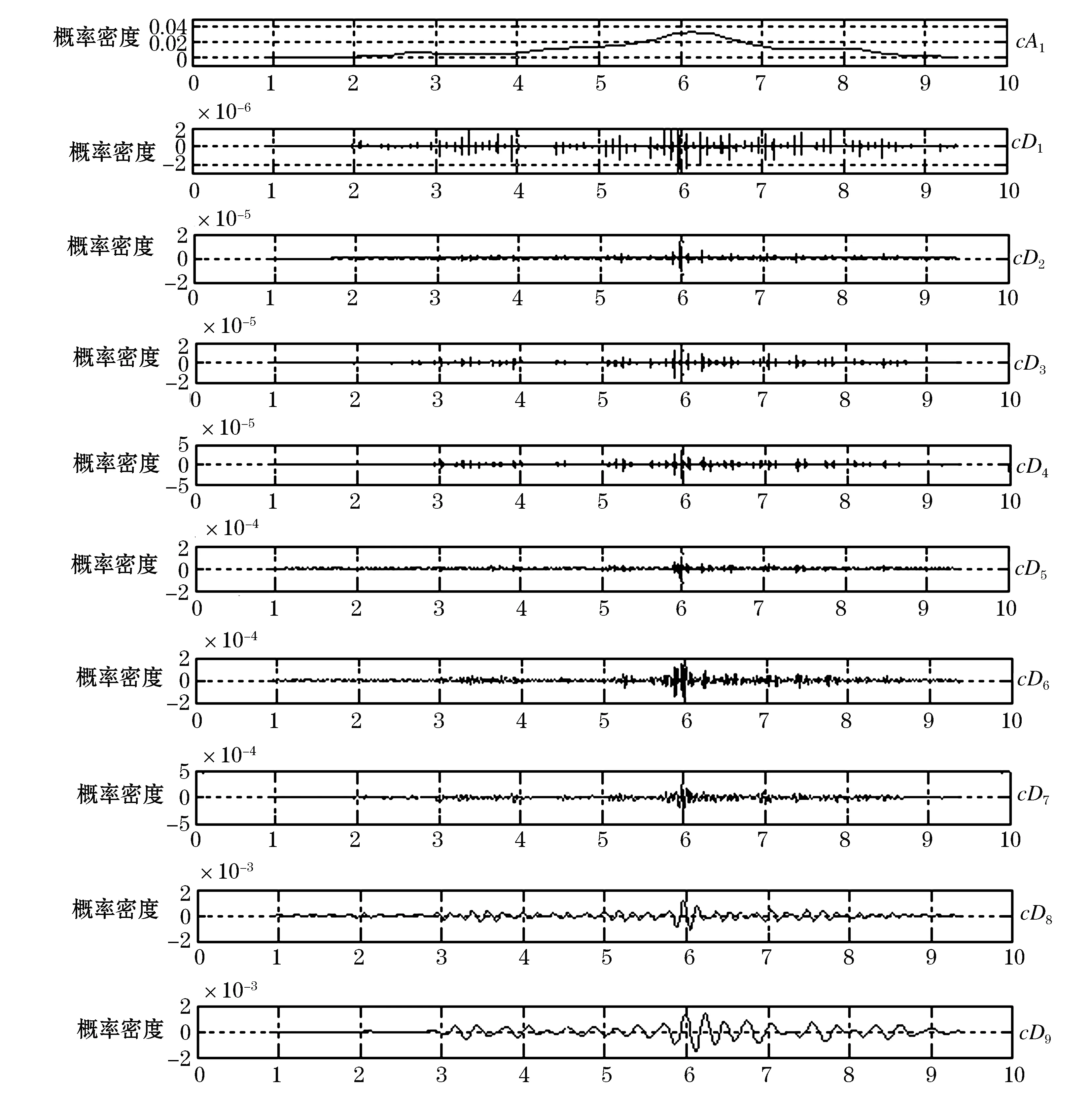
图5 换流站电流3 s有效值平方的小波分解Fig.5 Wavelet decomposition for 3 s RMS square of current in convertor station
200 ms换流站电流有效值平方的概率密度函数如图6所示。从图6可以看出,与牵引站的规律相似,200 ms换流站电流有效值平方继承了小波分解的低频部分,即近似系数cA1的部分,滤除了部分高频分量。
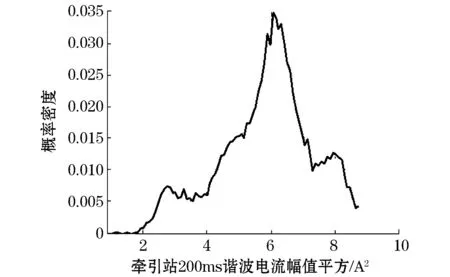
图6 换流站电流200 ms有效值平方的概率密度Fig.6 Probability density for 200 ms RMS square of current in convertor station
6.3 风电场电能质量数据分析
图7为风电场3 s谐波电流幅值平方的概率密度函数,分布为较为平整,近似于高斯分布。
对图7做小波分解,可以将其分解为如图8所示的分量概率密度,与换流站分解结果相差较大。主要原因是换流站电流分布较为陡峭,分解变量含有较多的高频分量。而风电电流幅值平方分布较为平滑,分解分量比较少,且含有的低频分量较多。说明小波分解对不同非线性负荷分布具有一定的适应性,可以根据不同的负荷特性分解出不同的分量,进而反映出不同负荷的特征。

图7 风电场电流3 s有效值平方的拟合曲线Fig.7 Fitting curve for 3 s RMS square of current in wind farm

图8 风电场电流3 s有效值平方的小波分解Fig.8 Wavelet decomposition for 3 s RMS square of current in wind farm
图9为经过变换之后200 ms风电电流有效值平方的概率密度函数,与图7所示的波形具有较好的相似性,说明200 ms有效值概率分布与3 s有效值概率分布具有较好的相似性。
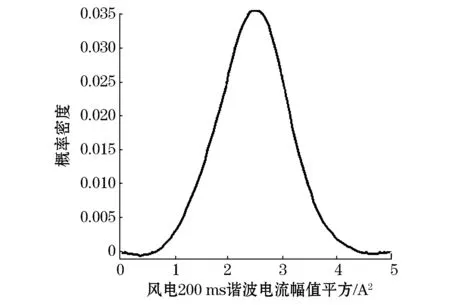
图9 风电电流200 ms有效值平方的概率密度Fig.9 Probability density for 200 ms RMS square of current in wind farm
从图1、图4、图7可以看出,对应不同的概率密度函数曲线,小波分解都可以有效地将对应的细节系数和近似系数分离处理,有效地估计200 ms值的概率密度函数,表明该方法具有较好的适应性,能够针对不同的非线性负荷进行概率密度函数的估计。
7 结 语
依据3 s有效值数据计算200 ms值概率密度函数。小波分解的引入简化了电能质量有效值概率密度函数估算。但仍有以下问题需要解决:
1)200 ms值的区间估计只是粗略假设,需要更为精确的理论评估来确定200 ms值区间。
2)小波基的选取缺乏最优的选择方法,有待于更加规范的反复选取。
