基于毕奥-萨伐尔定律的永磁球形电动机定子线圈磁场分布研究

韩 冰，米 震，马子刚，魏占朋

（1.国网天津市电力公司电缆分公司，天津 300171；2.国网天津市电力公司静海供电有限公司，天津 301600）

0 引言

涡流损耗会使永磁球形电机出现温升问题，在一定程度上会影响电机性能和寿命，因此，对永磁球形电机涡流损耗进行研究很有必要。文献［1-2］从定子线圈的电流密度入手，将定子线圈等效为位于线圈间隙的圆环电流片，并忽略电流片厚度，推导出永磁球形电机涡流损耗的表达式。这种方法适用于分布式绕制的定子线圈，集中分布式定子线圈产生的磁场与此不同。

法拉第电磁感应定律将通电后的定子线圈形成的磁场和涡流密度紧密地联系在一起，通过求解定子线圈磁场表达式即可求得涡流密度，根据涡流损耗与涡流密度之间的对应关系，最终可获得永磁球形电动机涡流损耗的解析表达式。因此，可从求解通电定子线圈所形成的磁场出发来分析研究，继而求解出电机的涡流损耗。

通电定子线圈所形成的磁场十分复杂，在可查的文献中有关定子线圈所产生的磁场问题的研究较少。关于普通永磁电机定子线圈的磁场研究多是借助于有限元方法，利用软件建立相对应的二维、三维有限元模型，对所建立的模型进行仿真分析［3-6］；或是根据所研究的电机的轴向对称性特点，对电机做进一步降维处理，将其简化为二维研究模型，在简化的基础上用矢量磁位的方法进行线圈磁场的求解计算［7-8］。由于球形电机的特殊结构，复杂的边界条件导致定子线圈磁场复杂，很难通过精确等效将其转化为二维模型。文献［9］通过磁场积分法对永磁球形步进电机定子线圈产生的磁场进行了分析，给出了相应的计算公式，但并未求解出具体表达式。文献［10］通过对永磁球形电机定子线圈进行暂态磁场仿真，说明了其磁场分布对涡流损耗有影响。文献［11］基于等效磁网络法，将永磁球形电机定子绕组等效为圆柱形永磁体，求解得到单个定子线圈在局部坐标系下的磁场表达式，但却没有给出所有定子线圈在全局坐标系的磁场分布。

永磁球形电动机如图1 所示。由定子和转子两部分结构组成，球形转子以输出轴为对称轴，上部镶嵌法兰盘，下部与底座相连，在转子赤道处环绕转子一周镶嵌6 块N、S 交替分布的永磁极，54 个采用集中绕制方式的定子线圈分3 层分别均匀分布在球形定子壳内。

图1 永磁球形电动机

针对定子线圈特有的结构，可以采用物理学中有关圆电流磁场的求解思路，首先求解出任意位置单个定子线圈在三维空间中的磁场分布，然后采用叠加定理求出永磁球形电动机所有定子线圈在三维空间的磁场分布。纵观国内外学者关于圆电流磁场分布的研究，为简化分析求解的难度，均是将坐标原点建立在圆环中心或其中心轴线上。采用目前文献所给出的建系方法求解空间中任意位置处的任一点的磁场问题对于研究者来说依然十分困难，因此，很多文献只是对圆电流的中心轴线、近轴区域［12-15］或是电流平面［16-18］上的磁场进行分析计算，有些文献对垂直于圆电流平面的磁场［19］或是圆电流远区处的磁场［20］进行分析研究。现如今虽然有一些学者对圆电流所在空间任意位置处的任一点的磁场进行了相应探究［21-24］，但同样是延续了之前的建系方法，只是建立了针对一个线圈的坐标系，在固定坐标系的基础上展开的求解计算。当所研究的磁场问题涉及同一个坐标系下对两个或多个分布在不同地点处的定子线圈所产生的磁场具体分布时，现有的分析方法是没有办法解决的。

本文所研究的永磁球形电动机的定子线圈，是沿定子球壳内部不同经度、纬度线相交点处的位置来放置的，在空间中任一点处的磁场是定子球壳内所有定子线圈所形成的磁场在同一个坐标系下磁场的叠加总和。根据所研究的实际永磁球形电机定子线圈设计特点，以图1 所示电机结构为模型建立以转子球心为坐标原点的坐标系，借鉴“割圆法”思想，在毕奥-萨伐尔定律的基础上，对任一位置处的单个定子线圈在空间任一点处所产生的三维磁场展开解析计算，得到单个定子线圈磁场的表达式，通过与有限元结果比对，验证了解析方法的正确性。

1 基于毕奥-萨伐尔定律求解单个定子线圈的磁场

根据永磁球形电动机的结构特点，以转子中心为坐标原点，建立如图2 所示的球坐标系。

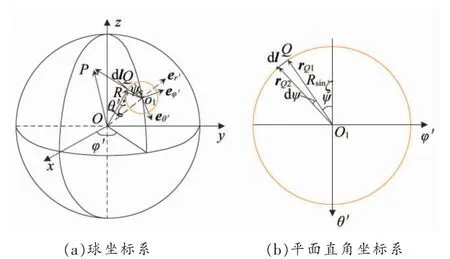
图2 任意位置定子线圈示意

图2（a）给出了空间任一位置处单个定子线圈在球坐标系中所处的具体位置，假设定子坐标与转子坐标重合。（r，θ′，φ′）为定子线圈位置在球坐标系下的表示，其中，r 表示坐标原点与定子线圈中心的距离，φ′表示x 轴正向与定子线圈中心轴线的夹角，θ′表示z 轴正向与定子线圈中心轴线的夹角。er、eθ′、eφ′为球坐标（r，θ′，φ′）的单位矢量，ζ 表示定子线圈的角径，R 表示球心到定子线圈边界点距离。图2（b）给出了以定子线圈中心为原点，以θ′和φ′为坐标轴，单个定子线圈在局部坐标系中的坐标图，ψ 为定子线圈边界点与中心点连线与θ′负半轴之间的夹角。

取定子线圈上任一点Q（x′，y′，z′），称作源点，I为定子线圈电流。根据毕奥-萨伐尔定律，源点Q 在空间任意点P（x，y，z）（称作场点）处的磁感应强度为

式中：μ0为真空磁导率；r′为由点Q 指向点P 的矢量；r′为由点Q 到点P 的长度；dl 是沿点Q 切线方向的长度微分矢量。

在空间任一点P 处，定子线圈所形成的磁感应强度B 的表达式为

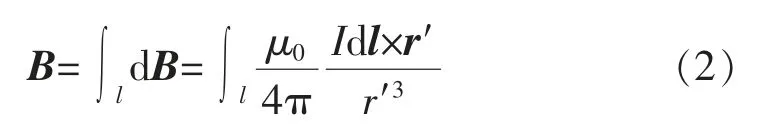
图2 中的矢量可表示如下：

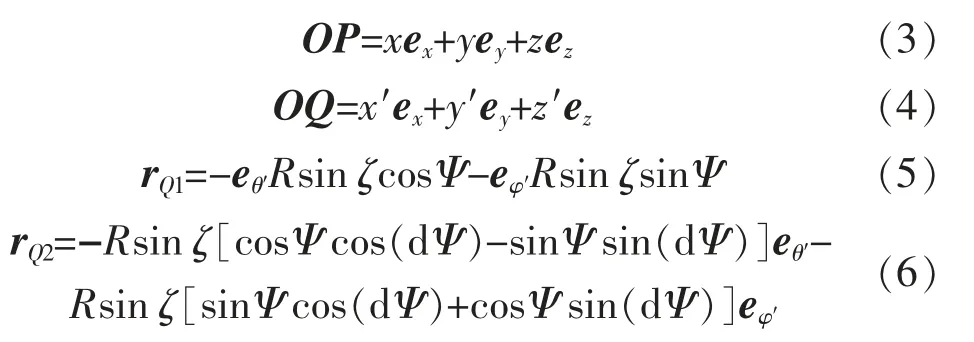
在式（5）—式（6）中，dΨ 取值较小，因此，cos（dΨ）近似等于1，sin（dΨ）近似于dΨ，经上述近似，rQ2表达式为

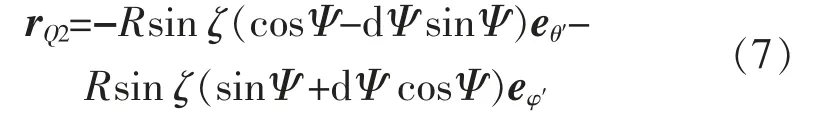
由rQ1、rQ2得dl 表达式为

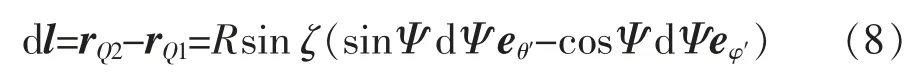
将式（3）—式（4）代入，得r′表达式为：

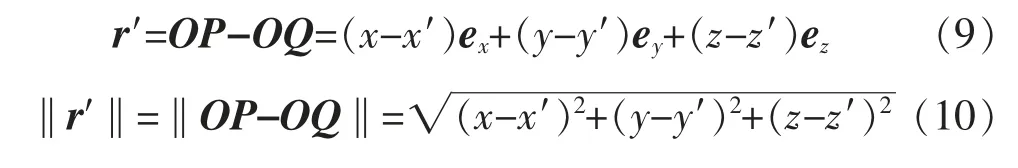
根据球坐标系与直角坐标系两个坐标系下单位矢量之间的变换关系，可以得到式（11）。

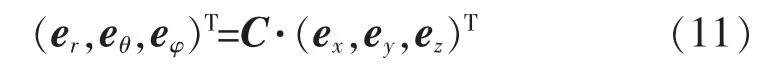
变换矩阵C 为

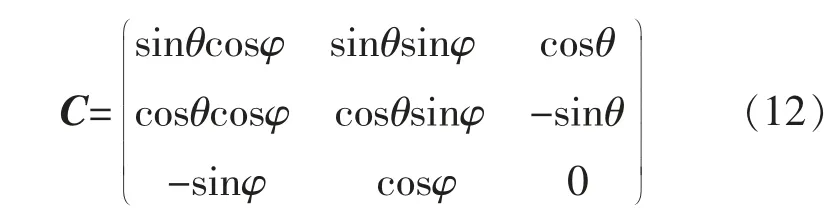
将式（11）和（12）代入式（8）后得

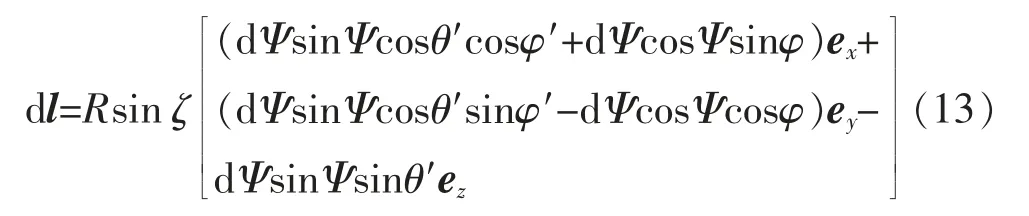
源点Q 在球坐标系和直角坐标系中的坐标变换关系为：

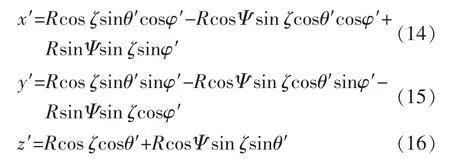
根据球坐标系与直角坐标系两个坐标系下单位矢量之间的变换关系，可得场点P 在这两个坐标系间的关系表达式为

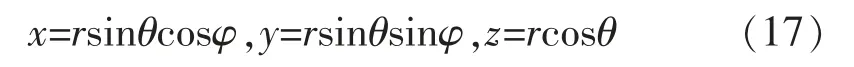
将式（14）—式（17）分别代入式（9）和式（10）整理得：

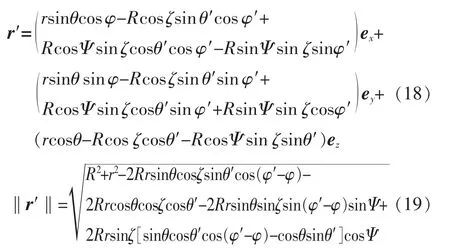
将式（13）、（18）、（19）代入式（2）得

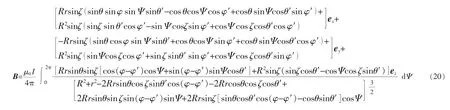
由式（20）可知，直接对含有三角函数和高次幂函数的分数进行积分很困难，因此，有必要寻求更为简单的求解方法代替直接积分法。

2 借鉴“割圆法”思想求解单个定子线圈的磁场

在求解圆的周长时，我们往往采用“割圆法”。所谓“割圆法”，其实就是画一个内接于圆形的正N 边形，通过不断倍增内接正多边形的边数，该内接正多边形的周长会越来越逼近圆周长，当N→∞时，此时圆的周长可以近似用该正多边形的周长代替。在分析求解本文圆柱形定子线圈的磁场问题中，可以借鉴“割圆法”思想。

根据图2（b），取dl 的中心点作为源点，将定子线圈N 等分，eθ′的负半轴为起始段，沿逆时针，分别记为第1，2，3，…，N 段，其中，第n 段的中点记为Qn。当N 趋于无穷大时，采用叠加定理，即可得到定子线圈在点P 产生的磁场如式（21）所示。

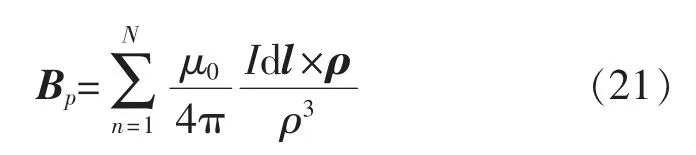
式中：ρ 为由点Qn指向点P 的矢量；ρ 为由点Qn到点P 的长度。

记Ψn为Qn与定子线圈中心点的连线与eθ′负半轴的夹角，可表示为

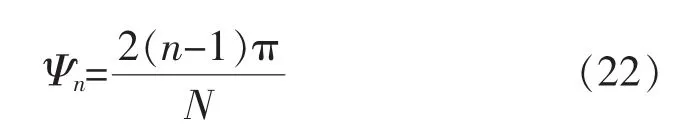
按照上述分割方法可得第n 段圆弧段的上下端点。

上端点为

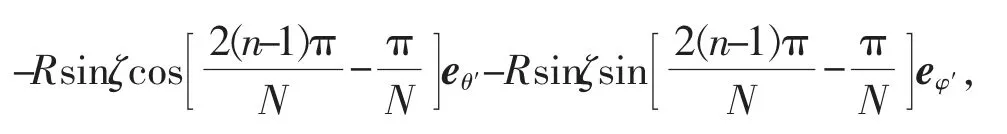
下端点为

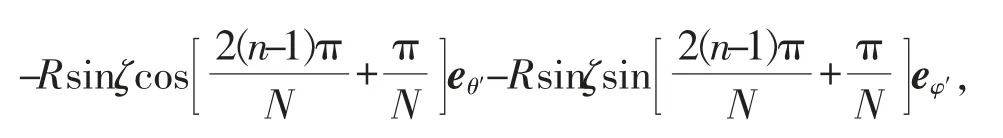
因此，

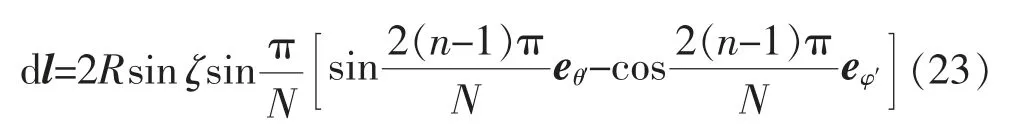
由式（11）和式（12）得

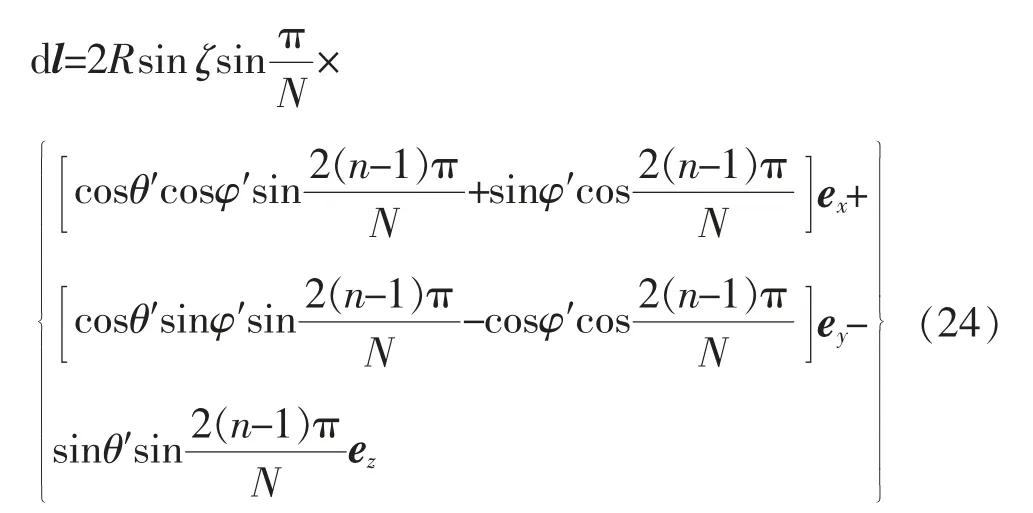
将式（24）以及Ψ 换作Ψn的式（18）—式（19）代入式（21）得

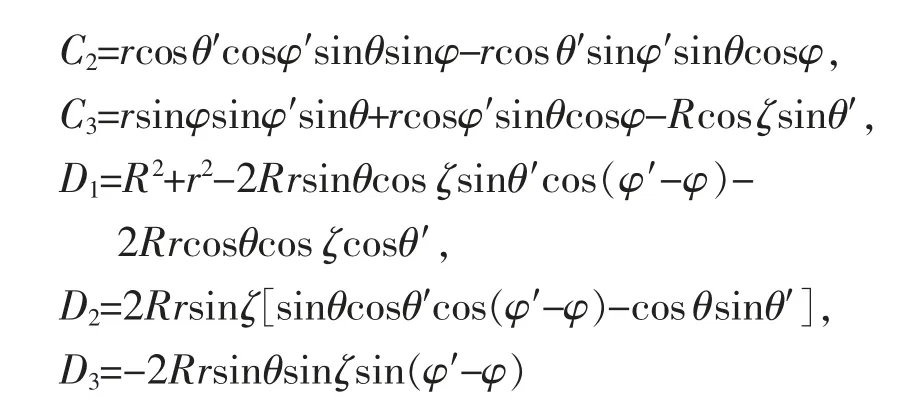
将上述简写表达式代入式（25），可得所研究的永磁球形电机柱形定子线圈在空间任一点处的磁感应密度各个分量的表达式为：

式中：从x 轴正向望去，当定子线圈线电流密度为逆时针时，式（26）—式（28）取“+”，反之，式（26）—式（28）取“-”。

3 算例分析

3.1 单个定子线圈中心轴线上的磁场

当场点P 坐标为（r，θ′，φ′）时，得任意位置单个定子线圈中心轴线上的磁感应强度：

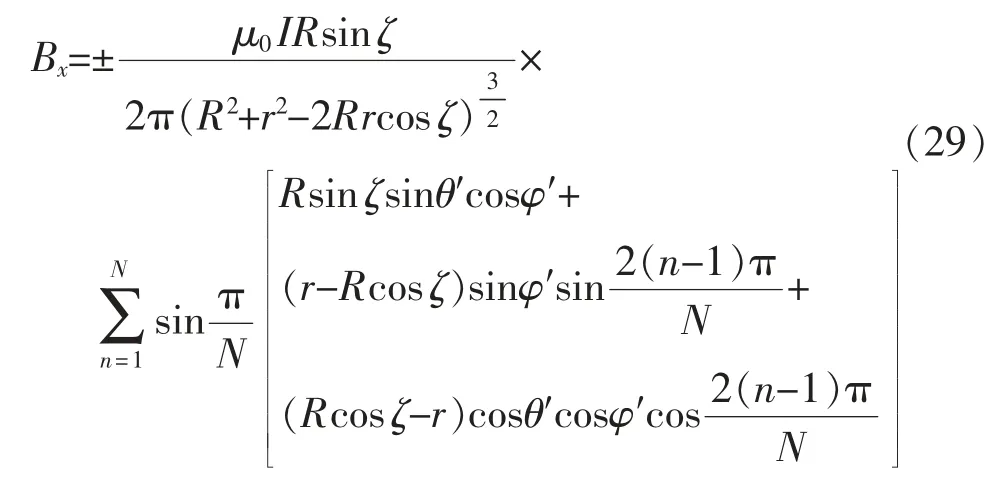
式中：R′=Rcos ζ，表示文中所研究的定子线圈的半径。

当θ′=90°，φ′=0°时，式（32）—式（34）为

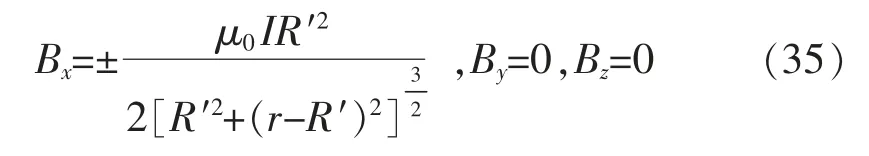
可知定子线圈中心轴线上无y、z 方向上的磁场分量。与文献［12-16］所得结论相比，两者的结果是一致的，说明研究定子线圈所借鉴的“割圆法”是可行的。

3.2 数值算例

表1 给出了所研究定子线圈的各项参数，其中，分割段数N 取1 000，电流方向取顺时针方向。

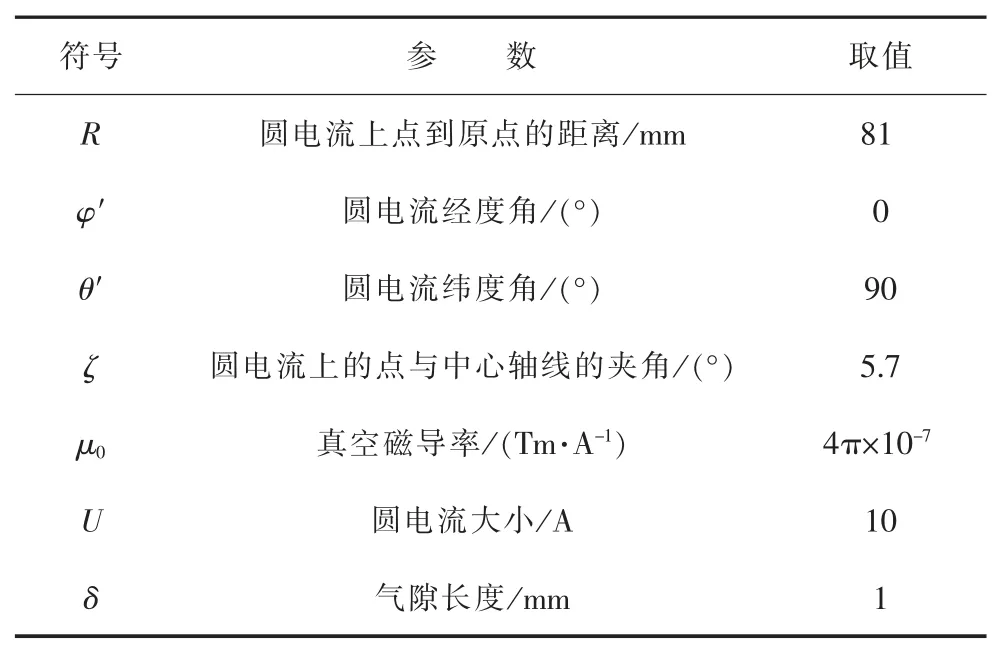
表1 定子线圈各参数

图3 给出了定子线圈磁场在r=80 mm 的半球面上随经度角和纬度角变化的情况。

从图中可以看出，当固定经度角或纬度角时，x 方向磁场以θ=90°的纬度线或φ=0°经度线作为对称轴呈对称分布；当固定纬度角时，以该固定纬度角处的纬度线与φ=0°所对应的经度线的相交点作为对称点，y 方向上的磁场呈中心对称分布，z 方向的磁场以φ=0°所对应的经度线为对称轴呈对称分布；当固定经度角时，以θ=90°的纬度线为对称轴，y 方向的磁场沿该对称轴对称分布，z 方向的磁场则以该固定的经度角处的经度线与θ=90°所对应的纬度线的相交点作为对称点，呈中心对称分布。

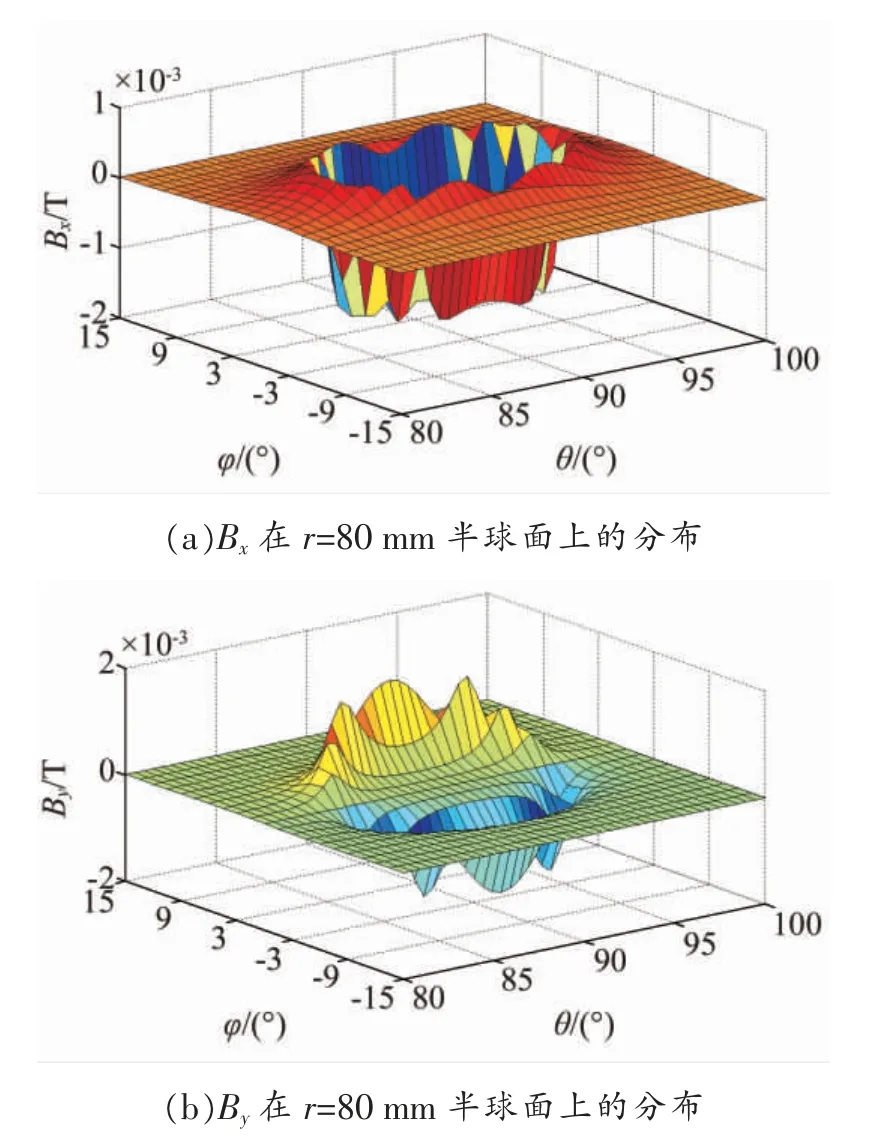
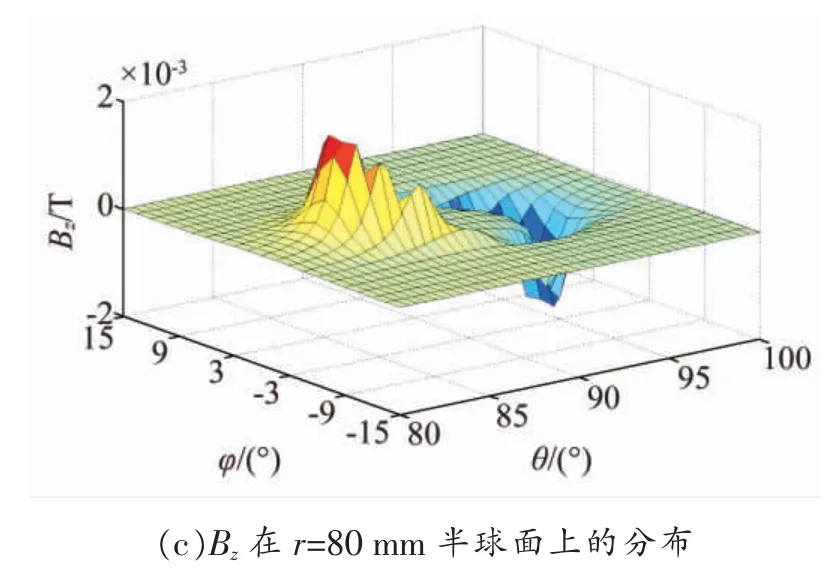
图3 r=80 mm 半球面上磁场分布图

图4 给出了φ=3°，θ=85°时，定子线圈磁场随r的变化情况。

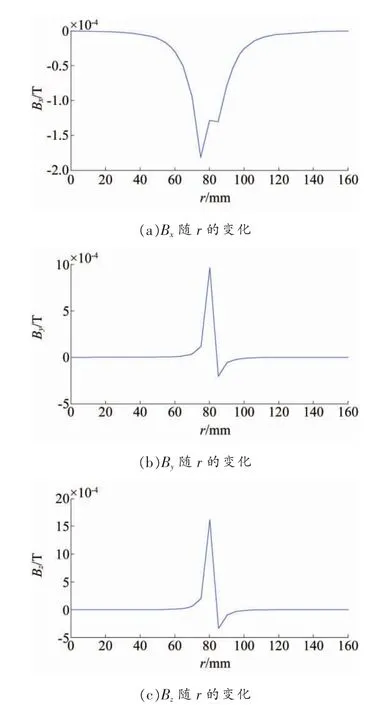
图4 磁场随r 的变化

由图4 可知，Bx、By、Bz随着离定子线圈距离的增大而迅速减小，仅仅在定子线圈中心及附近区域，磁场各分量比较大。

综上，所研究的柱形定子线圈产生的磁场在线圈附近区域数值较大，随着距离的增加，磁场逐渐减弱，超过一定区域范围，磁场迅速衰减，几乎为零，且在定子线圈两侧，磁场分布规律一致。越靠近定子线圈，各方向磁场数值越大。

3.3 数值算例有限元仿真验证

为验证所得结果的正确性，下面通过选取不同路径上定子线圈的磁场分布特点分别与有限元方法所得结果一一进行对比。图5 给出了定子线圈中心轴线上的磁场对比。

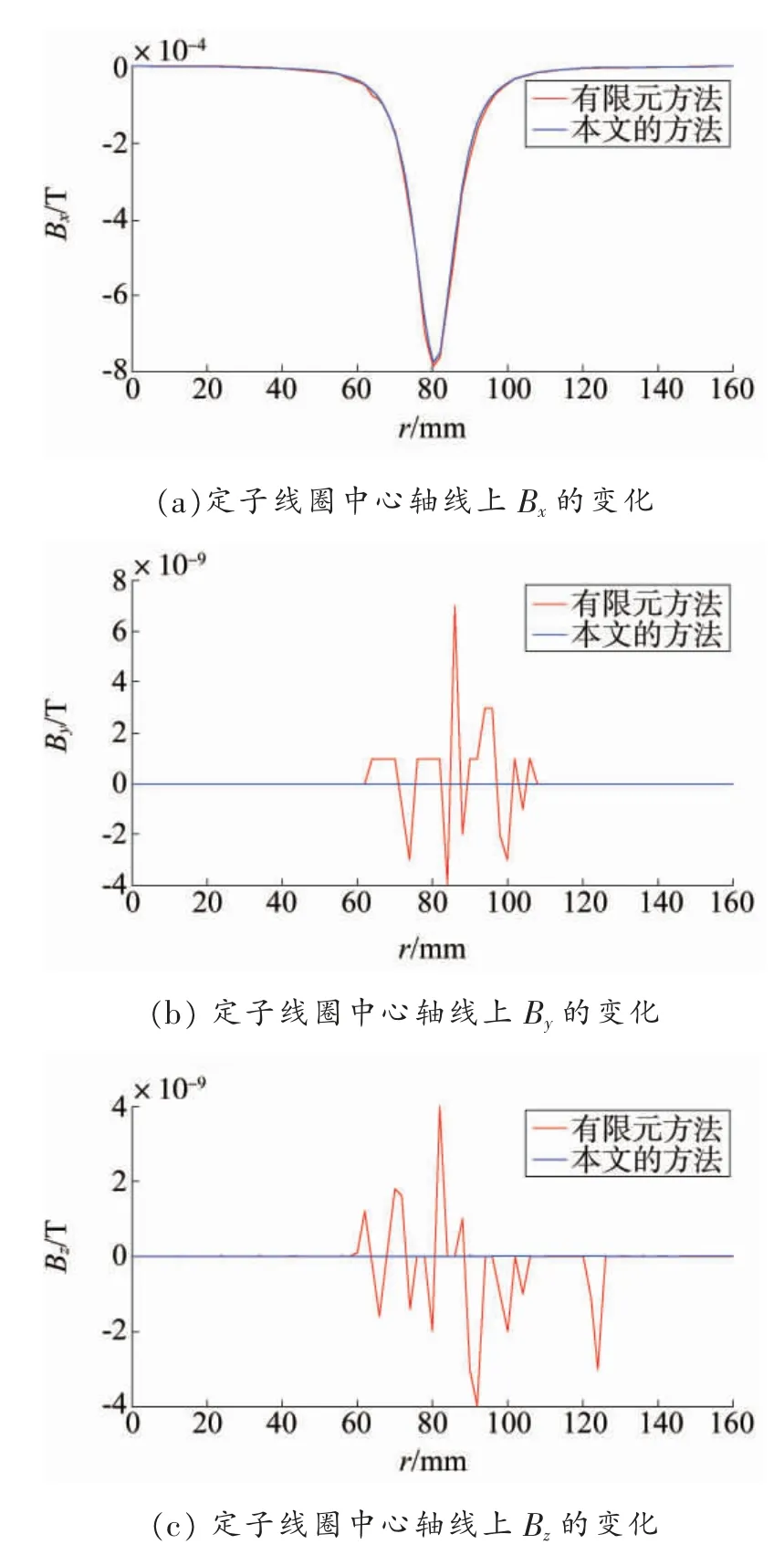
图5 定子线圈中心轴线上的磁场

从图5 可以看出，采用本文方法所得结果与有限元方法所得结果相吻合。由于选取定子线圈的中心轴线作为场点，所以仅存在x 轴方向上的磁场，该结论与现有文献［19-22］一致。由图5（b）和图5（c）知，在近轴区，受磁场分布影响，y 轴和z 轴方向上的磁场呈高频浮动，然后迅速降到零值，如果忽略该影响因素，磁场也仅存在x 方向上。

图6 给出了定子线圈在r=80 mm，θ=90°，φ 从-90°～90°变化的半圆形路径上的磁场对比。

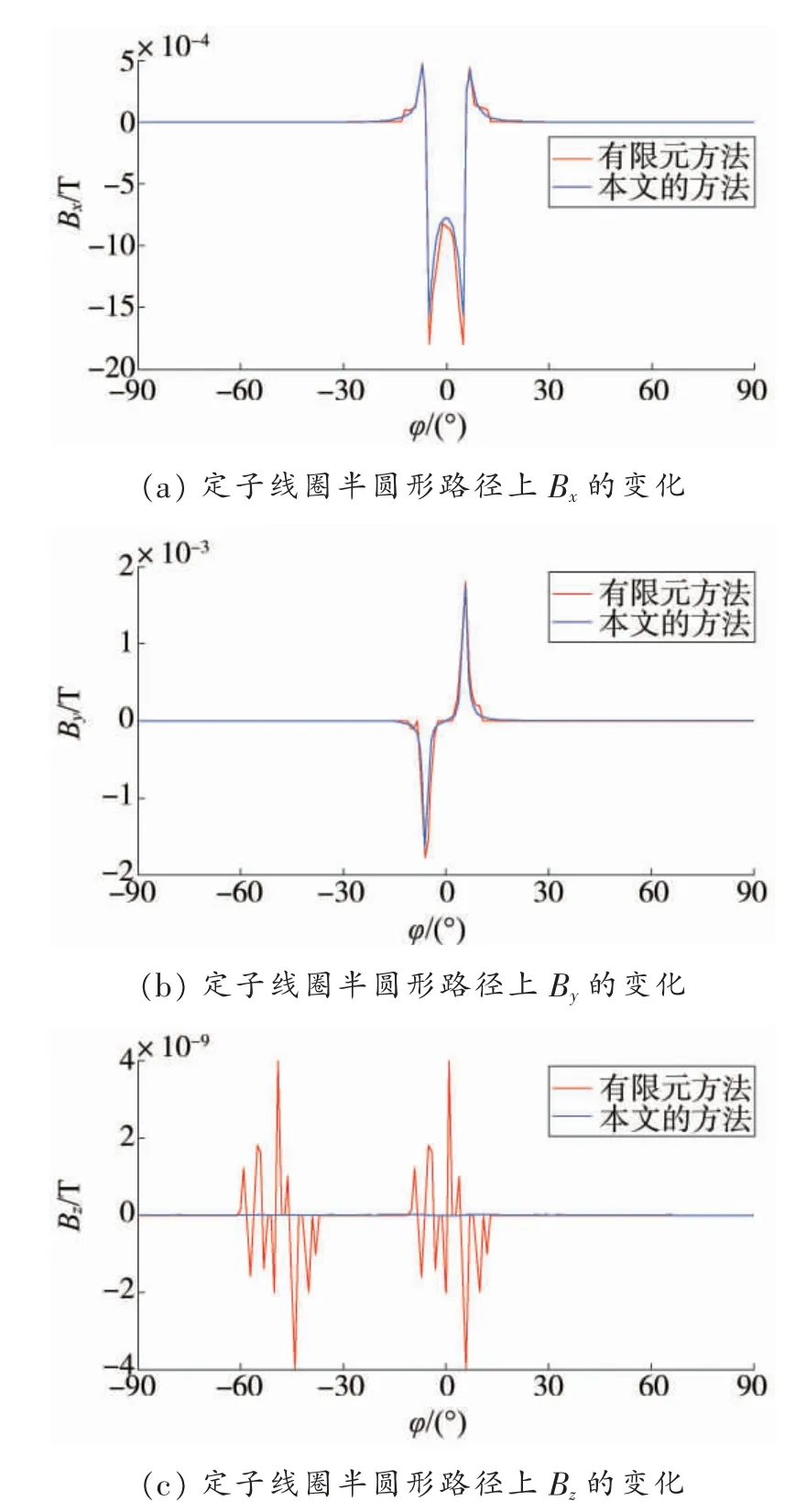
图6 定子线圈半圆形路径上的磁场

由图6 可知，由于定子线圈与xoy 面垂直，所选磁场路径位于xoy 面内，因此，Bx关于定子线圈中心轴线呈轴对称分布，By关于定子线圈中心点呈中心对称分布，Bz为0。

综上，通过定子线圈在不同的路径上的磁场具体分布情况图，可以看出，与有限元法所得结果近似一致，从而验证了研究方法的有效性。

4 结语

根据所研究的永磁球形电机柱形定子线圈的实际设计特点，将单个定子线圈的磁场问题看作物理学中所研究的圆电流的磁场问题，借鉴“割圆法”思想，在毕奥-萨伐尔定律的基础上，求解得到了单个定子线圈磁场的数值解表达式。通过选取了几个不同的路径上的磁场变化，与有限元结果展开对比，验证了所研究方法的有效性。

通过计算，可以得出定子线圈磁场在线圈附近区域数值较大，随着距离增加逐步减弱，当超过一定区域，定子线圈磁场迅速衰减为零的特点。为设计永磁球形电动机柱形定子线圈与转子之间的气隙长度提供参考。