高强度钢腐蚀管道极限承压能力评估方法

马 彬

(北京市燃气集团研究院，北京 100011)

1 概述

随着工业发展，石油和天然气的需求量逐年增加，对油气管道管线钢的强度等级的要求也越来越高。传统的评价管道极限承压能力的标准和方法由不同国家出台，且形成于不同时期，强度等级也不同，给使用带来不便［1－2］。由于高强度钢的失效机理与中低强度钢不同，采用传统的评价标准和规范预测偏差较大。因此，本文根据高强度钢的材料特性和失效机理，采用理论推导、有限元模拟、数值拟合和试验验证相结合的方法，研究适用于评价高强度钢腐蚀管道极限承压能力的预测方法。

2 无缺陷管道极限承压能力评估公式

2.1 条件设定

由于大多数管道处于埋地状态，为了便于评价公式的推导，对管道进行以下设定:管道相对于缺陷足够长。管道为薄壁结构。受土壤摩擦力，管道端部轴向位移为零。管道材料在塑性变形阶段，具有不可压缩性。管道仅受内压作用，不受其他外载荷。

2.2 管道应力

管道的内压为p，外表面受压力为0，考虑到管道的薄壁结构，径向应力可以忽略，即:

式中 σrr——径向应力，MPa

环向应力σθθ的计算式:

式中 σθθ——环向应力，MPa

p——管道内压，MPa

do——管道外直径，m

δ——管道壁厚，m

轴向应变εaa的计算式为:

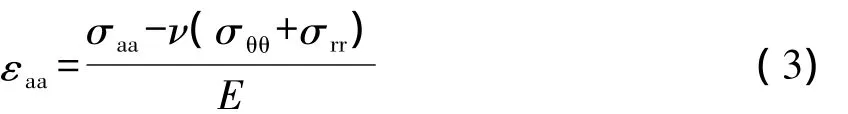
式中 εaa——轴向应变

σaa——轴向应力，MPa

ν——钢材泊松比，考虑塑性条件下体积不可压缩，取 0.5

E——钢材弹性模量，MPa

由于管道两端固定，因此轴向应变为0，则由式(2)、(3)可得:

由此可得到范式(Von Mises)等效应力σM的计算式为:

式中 σM——范式等效应力，MPa

2.3 管道应变

由塑性不可压缩性可知:

式中 εrr——径向应变

εθθ——环向应变

由于轴向应变为0，由式(6)可得到:

径向应变εrr的表达式为:

式中 δp——管道原始平均壁厚，mm

环向应变εθθ的表达式为:

式中 do，p——管道原始的平均外直径，m

由此可得到范式(Von Mises)等效应变εM的计算式为:

式中 εM——范式等效应变

由式(7)～(10)可得到:

2.4 无缺陷管道的极限承压能力

根据式(5)、(10)、(11)结合 Ramberg－Osgood幂硬化模型［3］，在无缺陷管道极限承压工况(d p/dεM=0)下可得到无缺陷管道的极限内压p0:

式中 p0——无缺陷管道的极限内压，MPa

n——硬化指数

σ'u——拉伸强度，MPa

ε'u——应力达到拉伸强度对应的名义应变

3 腐蚀缺陷对管道极限承压能力的影响

采用非线性有限元模拟埋地管道实际工作情况，设计了195组不同缺陷尺寸、不同材料参数以及不同管道规格的有限元模型进行分析。内压由0逐渐加载至25 MPa。

关于体积型缺陷的宽度对管道的影响，相关研究发现［4－5］:缺陷宽度对管道失稳的影响并不明显，这是由于管道在爆破时所受的环向应力远大于轴向应力。因此，本文主要分析体积型缺陷的长度、深度对管道失效的影响。缺陷类型主要是孤立蚀坑、沟槽型缺陷。将长度和宽度较小的缺陷视为蚀坑，用椭球形来模拟(见图1)。对于修长的槽状腐蚀缺陷，采用沟槽进行模拟，为避免槽端部的应力集中，建模时槽的端部采用椭球形、槽身采用柱面(如图2)。

图1 椭球形蚀坑

有限元模型采用的3种管材的参数见表1。3种管材的弹性模量均为207 GPa，泊松比均为0.3。3种管材的规格及设计参数见表2。

图2 沟槽型缺陷

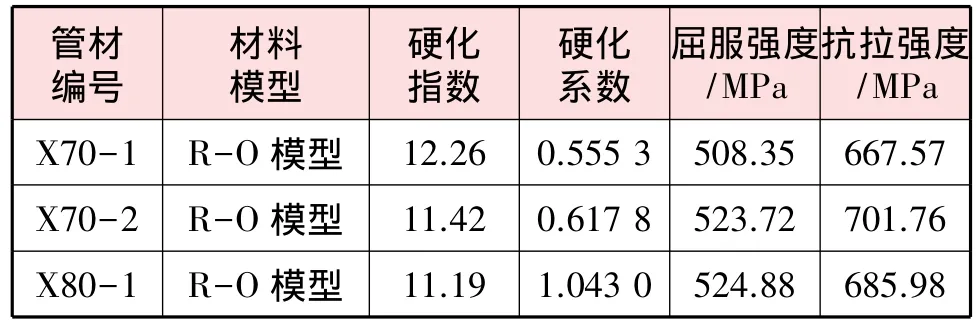
表1 有限元模型采用的3种管材的参数

表2 有限元模型采用的管道规格及设计参数

长度缺陷由20 mm至2 000 mm划分了13个长度等级，分别为 25、45、65、85、100、200、300、400、500、600、800、1 000、2 000 mm。深度缺陷分为 20%壁厚、30%壁厚、40%壁厚、50%壁厚、60%壁厚5个深度等级。13个长度等级分别与5个深度等级进行匹配(共65种组合，3种管材，即195组数据)，形成具有各自几何参数的体积型缺陷。

采用有限元模型计算出195组腐蚀管道极限承压能力。分析195组数据可知，在塑性阶段，管道缺陷最深处应力最为集中。缺陷长度一定的情况下，腐蚀管道极限承压能力随缺陷深度的增大呈线性下降。缺陷深度一定的情况下，腐蚀管道极限承压能力随缺陷长度的增大呈指数函数形态下降，当缺陷长度增加到一定程度后(这个临界缺陷长度约等于管道的外直径)，腐蚀管道极限承压能力的下降速度几乎为零。

4 腐蚀管道极限承压能力评估公式

4.1 评估公式

腐蚀管道的极限承压能力评估公式的研究是建立在无缺陷管道极限承压能力评估公式的基础上的。腐蚀缺陷一般为体积型缺陷，基于腐蚀管道缺陷深度的变化，得到极限承压能力的上限为:原壁厚管道的极限承压能力。下限为:最小壁厚管道的极限承压能力，最小壁厚为相关标准规范中规定的管道壁厚。即:

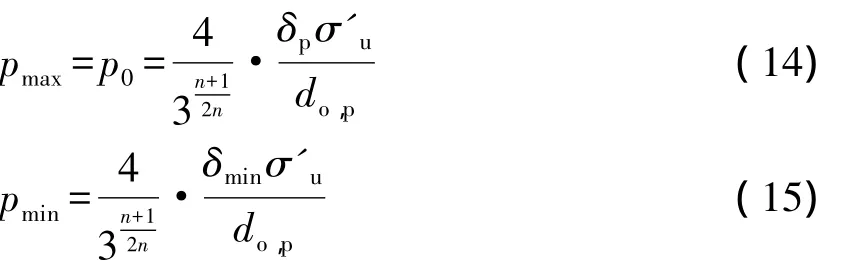
式中 pmax——腐蚀管道极限承压能力上限，MPa

pmin——腐蚀管道极限承压能力下限，MPa

δmin——最小壁厚，m

参照 PCORRC(Pipeline Corrosion Criterion，由美国Battle实验室开发的一种管道剩余强度评估方法)方法，腐蚀管道的极限承压能力plim的表示式为:

Δδ——缺陷深度，m

L——缺陷长度，m

根据腐蚀缺陷的几何参数对管道失稳的影响规律，以及边界条件:当Δδ、L均为0时(即无缺陷)，极限承压能力为pmax，此时影响函数f为1。当L非常大或Δδ接近δ－δmin时，极限承压能力接近pmin，此时影响函数f为0。参照PCORRC方法，影响函数f的形式确定为:

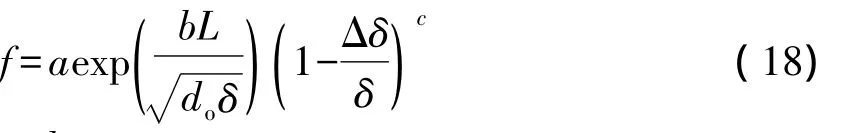
式中 a、b、c——待定参数

根据195组有限元模型计算结果，采用MATLAB拟合方法得到待定参数 a、b、c分别为0.750 1、－0.417 4、－0.115 1。将待定参数代入式(18)，并由式(17)得到腐蚀管道的极限承压能力计算式。

4.2 公式的验证

根据文献数据，将采用腐蚀管道的极限承压能力评估公式的计算结果以及美国机械工程师协会ASME B31G标准、挪威船级社 DNV F101标准、PCORRC方法的评估结果与真实爆破压力进行对比分析。真实爆破压力来自79组不同强度等级的腐蚀管道爆破试验数据，其中低强度等级钢(钢材X42～X56)数据出自文献［6］、［7］，中强度等级钢(钢材X60～X65)数据出自文献［8］～［13］，高强度等级钢(钢材 X70及以上)数据出自文献［14］、［15］。

由比较结果可知，在腐蚀管道的极限承压能力评估中，对于低强度等级钢(X42～X56钢材)，ASME B31G标准的评估结果更接近真实爆破压力。对于中强度等级钢(X60～X65钢材)，评估公式法、DNV F101标准、PCORRC方法的评估精度比较理想且大致相当。对于高强度等级钢(X70及以上钢材)，评估公式法的评估精度更理想。

5 结论

在塑性阶段，管道缺陷最深处应力最为集中。缺陷长度一定的情况下，腐蚀管道极限承压能力随缺陷深度的增大呈线性下降。缺陷深度一定的情况下，腐蚀管道极限承压能力随缺陷长度的增大呈指数形态下降，当缺陷长度增加到一定程度后(这个临界缺陷长度约等于管道的外直径)，腐蚀管道极限承压能力的下降速度几乎为零。

对于低强度等级钢(X42～X56钢材)，ASME B31G标准的评估结果比较接近真实爆破压力。对于中强度等级钢(X60～X65钢材)，评估公式、DNV F101标准、PCORRC方法的评估精度比较理想且大致相当。对于高强度等级钢(X70及以上钢材)，评估公式的评估精度更理想。