羊毛筒子纱染色的渗透性及其匀染性

2020-03-16王树根周嫦娥

毛纺科技 2020年1期

周伟，王树根，孙昌，周嫦娥

(江南大学纺织服装学院，江苏无锡 214122)

羊毛筒子纱染色浴比小，既能节约能源又能减少污染，而且乱纱少，纱线制成率高，易形成规模生产，是多品种、多花样、快交货的一种有利染色方法。但是目前国内羊毛筒子纱染色在生产中应用较少，主要原因是染色产品质量不稳定，没有完善的工艺参数，存在的关键问题是匀染性差，表现形式为筒子纱沿直径方向出现无规律色差、同一染缸中筒与筒之间产生色差、不同染缸之间成品产生色差[1-2]。一旦出现较大色差，需进行颜色修正，即使采用纱线剥色重新染色也很难达到匀染效果，导致了生产时间延长、影响销售，同时也增加了染色成本及纱线消耗，降低了纱线强力[3-4]。匀染效果差是筒子纱染色的共性问题，由于羊毛原料成本高，该问题成为羊毛筒子纱染色大规模生产的主要障碍。

研究表明，羊毛筒子纱染色出现色差与染色工艺、纱线密度及质量、设备、操作、水质等有关。目前研究者主要把目光集中在染色工艺方面[5-6]，对染色温度、pH值、染色时间等的研究较为深入[7]。本文构建一个由染液流体、纱线状态和产品匀染性三者相互结合的体系，分析染液流体与纱线、染液流体与染色相互作用关系，为解决羊毛筒子纱染色过程中色差问题提供理论支持。

1 实验部分

1.1 实验材料与设备

实验材料：18.8 tex羊毛纱线(张家港牧羊人服饰有限公司)。

实验药品：尤纳素红CQ(上海雅运纺织化工股份有限公司)，醋酸、醋酸钠、氨水(分析纯)，醋酸/醋酸钠缓冲溶液(pH值为4.5)。

实验设备：Colortec-2万能染色机(英国Advanced dyeing solutions有限公司)、AH-1000精密移液器(奥豪斯仪器有限公司)、STARTER 2100精密pH计(梅特勒-托利多仪器有限公司)、Datacolor-650反射分光光度仪(美国Datacolor公司)、SMARO-I络筒机(青岛宏大纺织机械有限责任公司)、SME301-Ф1500筒子纱脱水机(泰州宝进机械制造有限公司)、101-2AB鼓风干燥机(上海安亭科学仪器有限公司)。

1.2 单向染液流体耦合渗透实验

络筒：利用络筒机按照同一密度对羊毛纱线进行络筒[8]。

实验方法：采集万能染色机泵出口与入口压力差数值。具体实验方法：①设置万能染色机运行程序，单向染液流体流速为9 L/min，方向从筒子纱内到外，保持缸内水与纱线最上端在同一水平，且染液流体温度为室温；②将络好的羊毛筒子纱放入缸中，密封缸口并开始实验，待压差值稳定后记录泵两端压力差值，完成一次实验；③改变羊毛筒子纱厚度，重复以上步骤。④改变羊毛筒子纱络筒密度重复实验。万能染色机工作原理图见图1。

①—泵；②—加热室；③—染色缸；④—pH值探针；⑤—加料缸；⑥—流速仪。

1.3 染液流体染色实验

实验准备：①络筒时保持每次羊毛筒子纱厚度相同，在此基础上设置纱线密度作为变量。②调节万能染色机染色程序(定义正循环染色：染色方向从内到外；反循环染色：染色方向从外到内)。

染色处方：尤纳素红CQ 2%(owf)，浴比1∶16.5，醋酸/醋酸钠调节染液pH值为4.5，40 ℃入染，以2 ℃/min升温到98 ℃保温60 min[9]。固色时用氨水调节pH值为8.5，保温90 ℃固色20 min。染色结束后降温，取出纱线，皂洗。再用50 ℃水洗10 min，然后冷水洗，脱水并烘干。染色工艺流程如图2所示。

图2 染色工艺流程

1.4 测试方法

1.4.1 压力差值测试

根据图1，单向染液流体穿过具有一定厚度的纱线前后会产生压力差，通过万能染色机设备系统显示出染液流体压力差数值。

1.4.2K/S值测试

染色后按纱线厚度分成若干层，将各层解筒并织成布片。采用反射分光光度仪(Datacolor-650)测试K/S值。仪器参数设置：微小孔径，含镜面反射，D65光源，10°视角。K/S值是表征染色后羊毛纱线颜色深浅的重要指标，K/S值越大说明羊毛纱线得色越深[10]。

1.5 色差评价

根据每组实验所得纱线各层K/S值，计算其标准偏差和极差，标准偏差和极差越小，纱线染色的匀染性越高。

2 结果与讨论

2.1 羊毛筒子纱染液流体耦合渗透性分析

2.1.1 渗透性的数学表达

基于Biot的三维固结理论分析羊毛筒子纱与染液流体耦合过程中的渗透性能，Biot的三维固结理论是最早考虑多孔介质在三向压缩情况下渗流的流固耦合问题[11]。根据Biot的三维固结理论，单向染液流体渗透纱线过程中由于纱线应力和纱线孔隙压力相互作用而引起孔隙变化,可以简单理解为单向染液流体对纱线产生压力进而对多孔介质变形有影响。因此对羊毛筒子纱线这种可变性弹性多孔介质,羊毛纱线介质的本构方程及纱线之间的孔隙变化的响应方程为：

eij=2GΧij+wij(λXv+Tp)

(i,j=1,2,3)

(1)

式中：eij为羊毛纱线的总应力，Pa;Xij为总应变；Xv为筒子纱体积应变；p为纱线内部孔隙压强，Pa;wij为Kroncker函数记号；λ、G为拉梅系数；T为Biot常数。

水流冲击并渗透羊毛筒子纱线的过程一般近似于一维流动，忽略染液流体在纱线内部周向束缚，则筒子纱侧向变形及剪切应变均为零，所以只需考虑染液流体方向上的一维应变[12-13]。设羊毛筒子纱线初始孔隙率为n0,n为瞬时孔隙率，Δn为空隙改变,则变形引起的孔隙变化量Δn=n-n0，对于线性多孔介质而言，Δn满足方程：

(2)

式中：T、Q为Biot常数；XX为筒子纱x方向体积应变。

染液流体冲击纱线过程中孔隙度的改变必然会导致纱线渗透系数的变化，考虑到单向染液流体渗透纱线过程中的渗透率是一直变化的，羊毛纱线渗透系数与孔隙变化存在函数关系，则孔隙流体流动符合Darcy定律:

(i=1,2,3)，k(n)=k(n0+Δn)

(3)

式中：qi为羊毛筒子纱微元体上水流量，L/min;Xi为羊毛筒子纱微元体上水流量三维坐标；k(n)为羊毛筒子纱线渗透率。

染液流体在渗透羊毛筒子纱过程中，沿筒子纱直径方向不同位置的流速、渗透率、孔隙率、压力等都是变化的，但是染液流体通过一个微元单位的流体质量是守恒的[14]。

当渗流的非线性较明显时，可令羊毛筒子纱线的渗透系数服从指数函数，由渗透率方程(4)表示。研究表明：渗透率方程大体上服从线性函数、半对数函数、对数函数或者指数函数。

(4)

式中:k0、A为反映各向同性羊毛筒子纱线渗透特性的常数；k1为羊毛筒子纱线的初始渗透率，md。

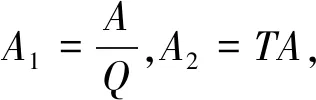
k(n)=k1eA1p-A2XX

(5)

由式(5)可知，在泵的作用下，单向流体进出纱线时产生的压力差与渗透率成反比关系，对于同一单向流体通过羊毛筒子纱线，压力差变化越大说明此时纱线的渗透率越低。

实验采用一维稳定渗流情形下控制羊毛筒子纱厚度的方法,初始水流速为q(L/min),筒子纱最内侧染液流体初始压力为p0(Pa),纱线最外侧处于染色缸内且流体压力为0[15-16]，每次实验控制应变为常量,则可以得到：

(6)

式中L为筒子纱厚度,mm。

由式(6)可见，羊毛筒子纱内部染液流体压力梯度并非常数，也非线性变化，表明筒子纱染色时各层纱线接触染料量一定不同，从而导致纱线内外层色差。结合式(6)推导结果，为了将渗透性数据计算简化并表征渗透性变化趋势，可将同一流速条件下的单向流体(初始压强p0相同)穿过羊毛筒子纱线过程中的渗透率变化情况用压力差变化进行表达。

2.1.2 耦合渗透性分析

对9 L/min流速的单向稳定染液流体穿过不同厚度的羊毛纱线在染色机泵进出口压力差数值进行分析，同时改变羊毛纱线的密度做平行实验,不同密度的纱线厚度变化对压差值的影响见图3。其中纱线密度计算公式为：

(7)

式中：m为纱线质量，g；ρ为纱线密度，g/cm3；h为纱线高度，h=14.5 cm；r为纱管半径，r=1.274 cm。

图3 不同密度的纱线厚度变化对压差值的影响

由图3可知：

①单向染液流体在渗透纱线的过程中受到了阻碍作用，表现为水流在泵入口压强与泵出口压强差值发生明显变化，随着纱线厚度增加，压力差负值逐渐变小。其中纱线厚度增加到90 mm的过程中压力差值下降较快，之后下降较为缓慢，最后趋于稳定。同时通过整体分析压力差值的变化情况，也可以间接地看出单向染液流体穿过某一厚度纱线的过程中其内部不同位置渗透性能是明显不同的，且下降趋势呈现先快后慢的现象，表明此过程中纱线孔隙度及渗透性是变化的。该现象符合理论分析，根据式(6)纱线厚度增加，压强的负值变化越大，同时根据式(2)(3)，纱线孔隙率与渗透系数是变化的，压强与渗透系数成反比例关系，渗透系数变小，下降趋势呈现先快后慢的现象。

②改变纱线密度，可以看出单向染液流体在渗透密度较大的纱线过程中，渗透性随纱线厚度的增加其数值迅速锐减，且变化范围较大。达到极限后，流体动能变小，难以渗透到纱线另一侧，若强行增加纱线厚度可能会使设备损坏。这是由于纱线密度增大，纱线内部孔隙变小，在初始水流量不变的情况下初始压强较大。由式(3)可以看出，初始压强大，流体渗透纱线过程中耗能大，对应的纱线初始渗透系数小。整体压强变大，而染液流体的流速在减少，势必导致渗透性减小，且变化迅速。

2.2 单向染液流体对羊毛纱线染后性能的影响

考虑羊毛纱线络筒密度不同对纱线染色性能影响较大，故将纱线密度作为变量，对厚度相同的纱线染色。染色后按纱线厚度分成若干层，将各层纱线解筒并织成布片，测得密度不同的2组纱线K/S值分布情况。并改变流体流速重复染色实验，得到羊毛纱线从里到外每层纱线K/S值分布曲线图，不同流速下单向染液流体染色后纱线的K/S值见图4～8。

图4 1.8 L/min流速单向染液流体染色后纱线K/S值

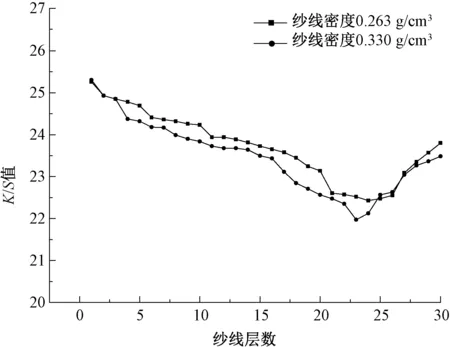
图5 3.6 L/min流速单向染液流体染色后纱线K/S值

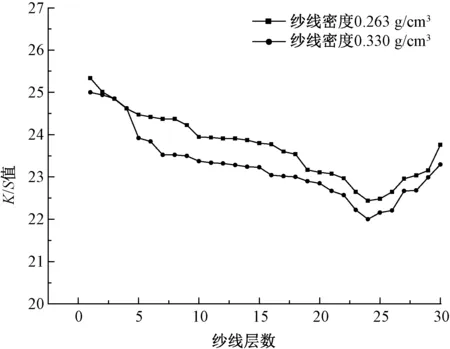
图6 5.4 L/min流速单向染液流体染色后纱线K/S值

不同流速的染液流体染色纱线后K/S值的标准方差和极差如表1所示。

分析图4～8及表1可知：

①随着纱层数的增大，从内到外纱线颜色表观深度对应的K/S值逐渐降低，且变化呈现先快后慢现象，最后稍微回升。这是由于纱线最外层浸泡在染缸中，染缸中的染液对羊毛筒子纱线最外层产生慢渗透的现象，从而导致最外层纱线出现K/S值回升的现象。

图7 7.2 L/min流速单向染液流体染色后纱线K/S值

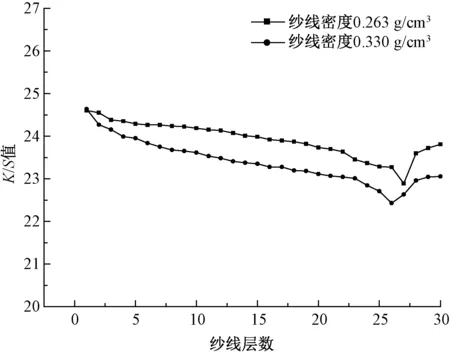
图8 9 L/min流速单向染液流体染色后纱线K/S值

表1 不同流速下单向染液流体染色纱线K/S值的标准方差和极差

②相同密度的纱线在受到同一流速单向染液流体染色时，密度大的纱线内部较为紧密，染色后纱线从内到外K/S值下降速度较快，且K/S值变化范围较大。由表1可以看出，染色条件相同情况下，密度小的筒子纱染色后K/S值的标准方差和极差较小，纱线匀染性较好。

③纱线密度相同的条件下，流速较大的单向染液流体对纱线进行染色时，染色后纱线从内到外K/S值曲线下降较平缓，且K/S值变化范围也相对较小；同时羊毛筒子纱染色后K/S值的标准方差和极差较小，表明在一定程度上改善了纱线匀染性。根据式(2)(3)，当染液流体流速变大，初始压强变大，使纱线的孔隙度变大，渗透性增强，最终K/S值变化平缓。

④在不同染色条件下，染色后K/S值最低点对应的层数有所差异，其中流速较大的染液流体比流速小的流体对纱线染色后K/S值最低点平均层数相对靠后。

⑤通过对单向染液流体对纱线染色K/S值分布曲线结果(图4～8)和图3耦合渗透性分析结果进行比对，发现其整体变化趋势完全相同,说明染液流体与纱线耦合渗流的过程中由于渗透性能的变化，导致染液上染纱线过程中纱线对染料的吸收能力不同，最终形成色差。

⑥这些现象与前述的耦合渗透性分析实验结论及理论公式相对应。

2.3 双向染液流体对羊毛筒子纱匀染性影响

2.3.1 正反循环染色对匀染性能的影响

为了探究反循环染色与双向染液流体染色对羊毛纱线染色后匀染性能的影响，采用5.4 L/min流速染液流体对0.33 g/cm3羊毛纱线染色，并作为不变条件。设置正循环(从内到外)、反循环(从外到内)及正反循环染色时间比为5∶5(5 min，5 min)的双向染色3组实验，染色纱线的K/S值测试结果见图9。

图9 5.4 L/min流速染液流体染色后纱线K/S值

由图9可以看出，运动方向不同的染液流体分别对纱线染色，沿染色方向纱线颜色表观深度变化趋势相同。根据实验所得纱线各层K/S值，计算其标准偏差和极差，如表2所示。标准偏差和极差越小，纱线染色的匀染性越高，反循环染色纱线K/S值标准偏差与极差较小，表明染液流体反循环对纱线染色后其匀染性相对较好；染液流体最先正循环开始染色，正循环与反循环染色时间比为5∶5(5 min，5 min)，染色后纱线匀染性比任一单向循环染色都好，证明正反循环染色相互结合的染色，可提升羊毛纱线的匀染性。

表2 染色后纱线K/S值的标准偏差与极差

产生这样结果的原因是：染色筒子纱从内层到外层,半径逐渐增大,各层容纱量也随之增加，但是单位时间内，不同位置的纱层面上通过的染液流量是相等的。当染液由内向外染色时,随着纱筒半径的增加纱的面积逐渐增加,单位面积上通过的染液减少(即流体线密度下降)。尽管染液流体的速度在一定程度上可以弥补纱线内深外浅的问题，但是纱线内外颜色表观深度差异依旧明显。当染液从外向内染色,染液流体线密度越来越大,有利于减少纱线内—中—外颜色表观深度差异，而二者结合可以弥补纱线中间色深较浅的情况，匀染性得以提高。

2.3.2 正反循环染色时间对匀染性的影响

由于正循环(从内到外)染色比反循环(从外到内)染色后纱线的匀染性差，探讨在流速5.4 L/min、羊毛纱线密度0.330 g/cm3条件下，正反循环染色时间比对纱线K/S值的影响见图10。

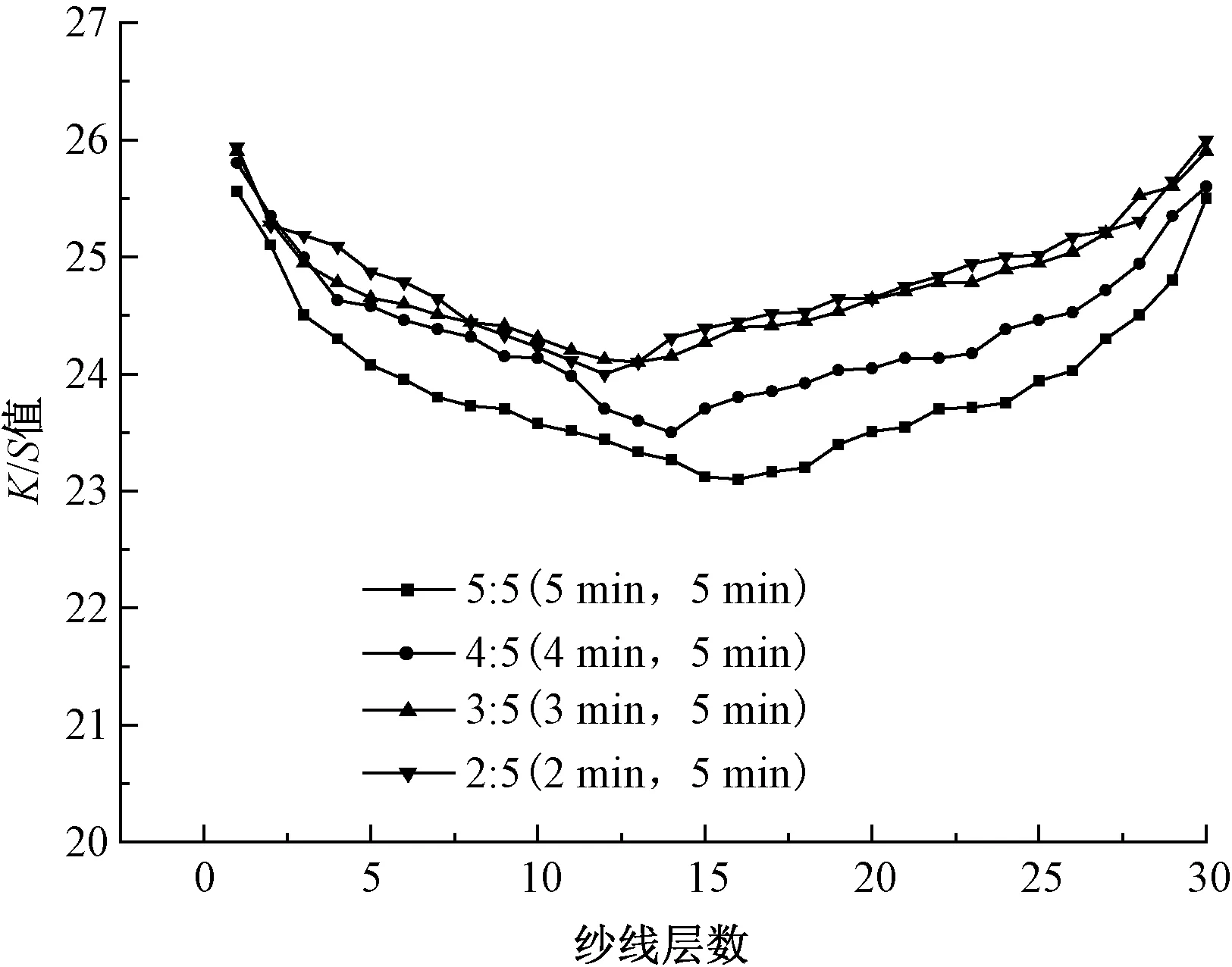
图10 正反循环染色时间比对纱线K/S值的影响

根据图10可得染色纱线K/S值标准差与极差，见表3。

由图10可以看出，染液流体正循环与反循环染色时间比从5∶5(5 min，5 min)到3∶5(3 min,5 min)的过程中纱线K/S值变化趋向平缓，且最低值逐渐上移；正反循环染色时间比为2∶5(2 min,5 min)时K/S值曲线下降速度变快，最低值稍有下降。且由表3可以看出，染色时间比为3∶5时K/S值标准偏差与极差最小，表明一定范围内增加反方向染色时间将可增加纱线匀染性，最佳正反循环染色时间比为3∶5(3 min，5 min)，但是若染液流体反循环染色时间较长会降低匀染性。

表3 不同时间比染色纱线K/S值的标准偏差与极差

2.3.3 正反循环染色顺序对匀染性的影响

在前述结论的基础上，保持同样的实验条件，由于反循环(从外到内)比正循环(从内到外)染色羊毛纱线的匀染性好，且正反循环时间比为3∶5时染得的纱线匀染性较好。为了探究染色顺序对纱线匀染性的影响，改变正反循环染色顺序测试对K/S值的影响，结果见图11。

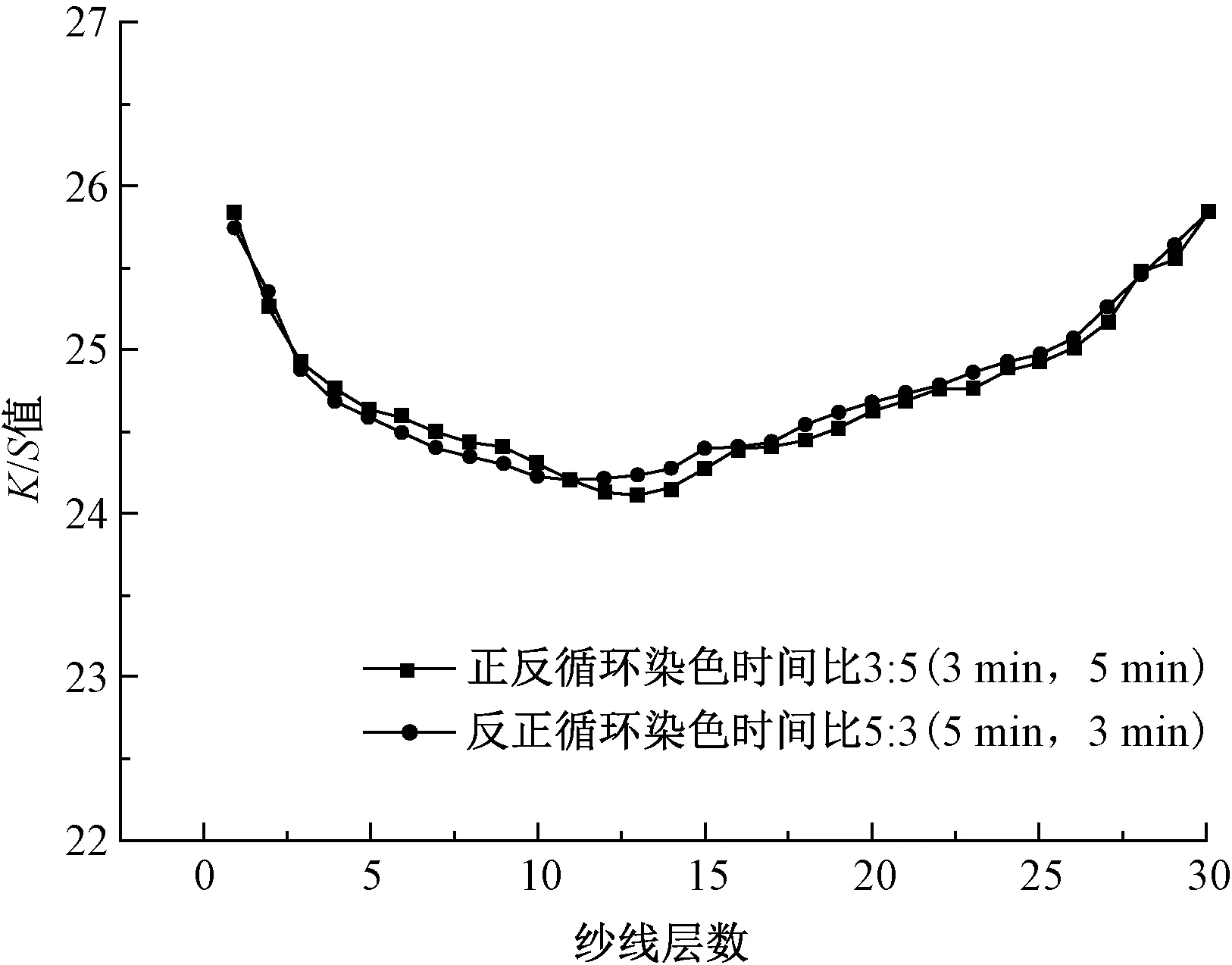
图11 正反循环染色顺序对纱线K/S值的影响

由图11计算得到正反循环染色时间比为3∶5(3 min,5 min)时，K/S值标准差与极差分别为0.500、1.8，反正循环染色时间比为5∶3(5 min,3 min)时，标准差与极差分别为0.499、1.7。

从反循环开始染色，反循环与正循环染色时间比为5∶3的染色条件下，染色后纱线K/S值变化曲线较平缓，且染色后纱线K/S值标准偏差与极差较小，表明其染色匀染性较好。

2.3.4 正反循环染色纱线厚度对匀染性的影响

为了探究纱线厚度对双向染液流体染色匀染性的影响，在2.3.3实验结论的基础上，反循环与正循环染色时间比为5∶3(5 min, 3 min)，其他条件不变，将纱线层数增加为45层，染色纱线K/S值分布见图12。根据图12计算得出标准偏差为0.708，极差为2.82。

图12 45层纱线染色后K/S值分布

对比图11、12可以看出，30层纱线相比45层纱线染色后颜色表观深度曲线下降平缓；30层纱线K/S值的标准偏差和极差相比45层纱线的数值更小，匀染性提高，说明染色时降低纱线厚度可以增加染后纱线匀染性。

2.3.5 升温速率对纱线匀染性的影响

羊毛纱线在一定温度以上时的上染速率较快，羊毛筒子纱染色时升温速率对染色纱线匀染性影响较大。为了探究染色升温速率对双向染液流体染色后匀染性的影响，保持其他条件不变，在反循环与正循环染色时间比为5∶3(5 min, 3 min)的条件下，升温速率对纱线K/S值的影响见图13。

图13 升温速率对染色纱线K/S值的影响

根据图13可得染色纱线K/S值的标准差与极差，见表4。

表4 不同升温速率染色纱线K/S值的标准偏差与极差

由图13可以看出，以3 ℃/min升温速率染色时，染色纱线的K/S值变化波动较大，且随着升温速率的下降，K/S值变化波动变小。由表4可以看出：在1 ℃/min升温速率的染色条件下，纱线K/S值的标准偏差和极差最小，匀染性能最佳，说明降低染色时的升温速率有利于提高纱线匀染性。

2.3.6 最佳染色工艺结果

在染液流体9 L/min流速条件下，对0.330 g/cm3密度的羊毛纱线染色，采用正反循环相结合的染色方式，反循环与正循环染液流体染色时间比为5∶3(5 min，3min)，染色升温速率为1 ℃/min，并选择纱线层数为30层，探究在此最佳染色工艺条件下纱线的匀染性能。最佳工艺条件下染色纱线的K/S值分布见图14。根据图14得出染色纱线K/S值标准差与极差分别为0.288、0.591。