基于分类的多机协同干扰航迹构造研究
2020-03-16唐家福穆平安巴燕阿依丁
唐家福, 穆平安, 巴燕·阿依丁
(上海理工大学 光电信息与计算机工程学院, 上海 200093)
组网雷达系统是采用两部或两部以上空间位置互相分离而覆盖范围互相重叠的雷达的观测或判断来实施搜索、跟踪和识别目标的系统,对组网雷达的干扰是电子对抗界的一个重要课题。航迹欺骗具有多种形式,相应的组网雷达亦有多种反欺骗策略。本文主要考虑距离假目标欺骗与同源性检验和数据融合之间对抗问题。文献[1-3]对距离假目标欺骗研究了相关硬件实现原理,因而本文不涉及相应的硬件实现。文献[4-5]都是建立了单架无人机欺骗单部雷达的基本数学模型并对求解算法进行优化,其中文献[4]采用勒让德伪谱法对模型进行求解,提高了求解模型的精度,文献[5]提出一种飞行器编队协同控制的虚假航迹产生方法,文献[6-7]研究了欺骗数学模型并对其进行优化,文献[8]对虚假航迹进行评估,提出一种基于距离模型的虚假航迹分析方法。这些研究大多对一条航迹的构造进行描述,本文从解析几何角度对产生多条航迹进行研究,采用分步优化、分类构造的策略,首先对已有航迹进行分析,使用尽可能少的无人机产生该航迹,再将所要产生的额外航迹分为两类,并证明两类航迹的存在性,利用剩余的无人机编队产生额外的航迹,最后对构造过程进行可视化仿真分析。
1 航迹距离欺骗原理
在组网雷达的信号跟踪和检测下,真目标与有源假目标在空间坐标上表现出一定的差异,在组网雷达统一坐标系中,真目标的空间位置是一致的,而对于有源假目标,组网雷达探测到的目标存在于组网雷达与无人机的连线及其延长线上,其空间状态主要由组网雷达的分布与无人机来决定,当不同雷达探测的目标在同一时刻其空间状态不一致时,则无法通过组网雷达数据中心的同源性检验,此目标则会被从数据中心中剔除。为了能对组网雷达实施有效干扰,针对同源性检验(本文考虑三台雷达的同源性检验),利用多架无人机对组网雷达进行协同干扰,如图1所示。同一时刻,多架无人机同时对组网雷达进行干扰,在组网雷达数据融合中心形成一个有效航迹点,多个航迹点即可形成一条航迹。通过协同控制无人机的飞行航迹,进而在组网雷达中心形成一条或者多条虚假航迹,从而完成欺骗目的,干扰敌方战略决策。
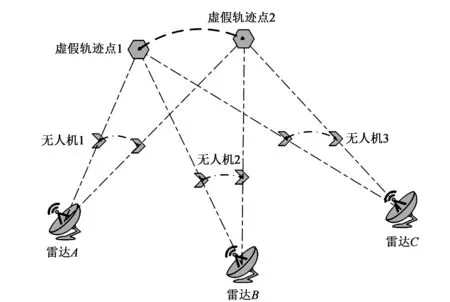
图1 航迹欺骗原理示意图
由图1可知,为了完成针对同源性检验的距离欺骗,应有如下基本假设:(1)干扰机具有一定的隐身能力不被雷达侦察到;(2)敌方雷达数量及其位置分布已知;(3)干扰机能够完成协同任务,并且能够实施干扰任务,即同一时刻一架干扰机能干扰一部雷达,在该部雷达接收机终端(数据融合中心)产生多个目标点,并且位于雷达与干扰机连线以及延长线上。
2 虚假航迹构造
2.1 拟产生虚假航迹分析
为了合理规划出至多条虚假航迹,首先应产生一条虚假航迹,其产生方法在许多文献中如文献[9]中都有涉及,或者根据对战策略进行产生。设构造的虚假航迹为N(Xi,Yi,Zi),包含n个时刻虚假航迹点的空间位置坐标,并对该虚假航迹进行分析。
图2给出了单架无人机、虚假目标点和雷达的几何关系以及在干扰过程中无人机可飞行区域的约束。
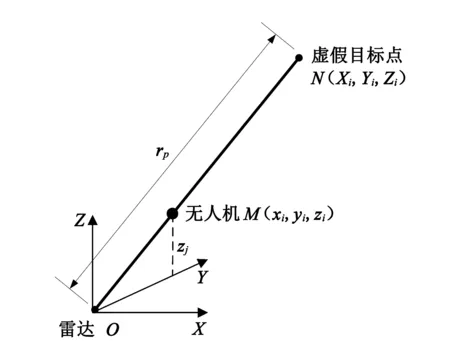
(a) 共线几何关系
(b) 无人机可飞行区域
无人机在第i个时刻的空间状态更新如式(1)所示:
(1)
其中(xi,yi,zi)为无人机空间坐标,(vx,vy)为平均速度,t=(N-1)T,T为地面雷达数据更新时间间隔,t为两个虚假航迹点之间的地面雷达数据更新时间的总和。速度约束和几何约束如式(2)所示:
(2)
其中v、vmax分别为无人机速度及速度最大值,H、Hmax、Hmin分别为无人机的高度、最大高度值、最低高度值,O、M、N分别为雷达位置、无人机位置、虚假目标点,λ为共线向量系数。
对于任意两架无人机,在同一时刻其间隔应小于ΔL,由此对无人机的飞行区域进行划分以确定zj,由式(1)、(2)可以求出无人机在第i时刻可以到达的极限位置,再通过向量共线几何约束求出目标位置,于是可以构造出一个判断矩阵T=(tij),tij表示一架无人机能否从i时刻所处位置到达j时刻的位置:
(3)
结合每一个地面雷达的判断矩阵T可以判断出至少几架无人机完成该虚假轨迹的构造。
2.2 第一类虚假航迹的构造
由2.1可以求出能构造出既定航迹的最少无人机数量。将剩下的无人机与已规划出的无人机协同以构造至多条虚假航迹。设构造既定虚假航迹的无人机集合为P1,未规划路径的无人机集合为P2。
第一类航迹定义为从P2中选择两架无人机与P1中无人机进行协同即可确定构造出的虚假航迹,第二类航迹定义为从P2中选择一架无人机与P1中无人机进行协同即可确定构造出的虚假航迹。
第一类虚假航迹的具体构造步骤如下:
(1)设2.1中航迹点为N(N1,N2,…,Nn),从中任意选取两点Ni、Nj,选取某雷达记为B,与Ni、Nj连线,在BNi、BNj中各取一点Mi、Mj,由向量几何约束得式(4):
(4)
其中λ1、λ2为共线向量基本定理的系数;
(2)通过另一雷达C与Mi、Mj组成平面,求平面CMiMj截取雷达中航迹点连线及其延长线可得到新的虚假航迹M,即解方程组(5):
(5)

2.3 第二类虚假航迹的构造
对于第二类轨迹的构造有两种策略,一种情况下是在第一类轨迹的基础上再构造第二类轨迹,另一种情况下是直接与P1集合中的无人机进行构造。为构造至多条虚假航迹,优先考虑后者。其具体构造过程如下:
(1)由于第二类只需要一架无人机的干扰,所以只要考虑对两台雷达进行干扰,设这两台雷达为E、A。在雷达E和Ni、雷达A和Nj组成的连线ENi、ANj上随机确定两点Mi、Mj满足式(6):
(6)
其中λ3、λ4为共线向量基本定理的系数;
(2)通过(1)中确定的两个航迹点Mi、Mj构造虚假航迹线N′,再向前后时刻等距直线延拓无人机轨迹点,得到N′的航迹点点集N′(Xi,Yi,Zi);
(3)由航迹点点集N′(Xi,Yi,Zi)确定无人机坐标位置,并且验证是否满足(2)式约束即验证矩阵T,若不满足条件则重新确定λ3、λ4,重新构造虚假航迹。
由于这种构造方法与P1进行协同飞行,存在一架无人机在某时刻参与既定虚假航迹的产生,而在下一时刻参与航迹N′的产生,在这两个时刻需要另外考虑是否能够到达这个问题,当不能到达时,则应该优先构造第一类虚假航迹,再构造第二类轨迹。
3 仿真分析
以9架无人机针对5部地面雷达的协同干扰为例,5部地面雷达的分布如表1所示,一条既定拟产生虚假航迹点坐标如表2所示,单条航迹可由文献[6-9]所提出方法构造,地面雷达数据融合中心将20个连续合理航迹点视为一条航迹。

表1 地面雷达位置分布

表2 既定虚假航迹点空间坐标
地面雷达数据更新时间间隔T=10 s,无人机速度约束为120 km/h
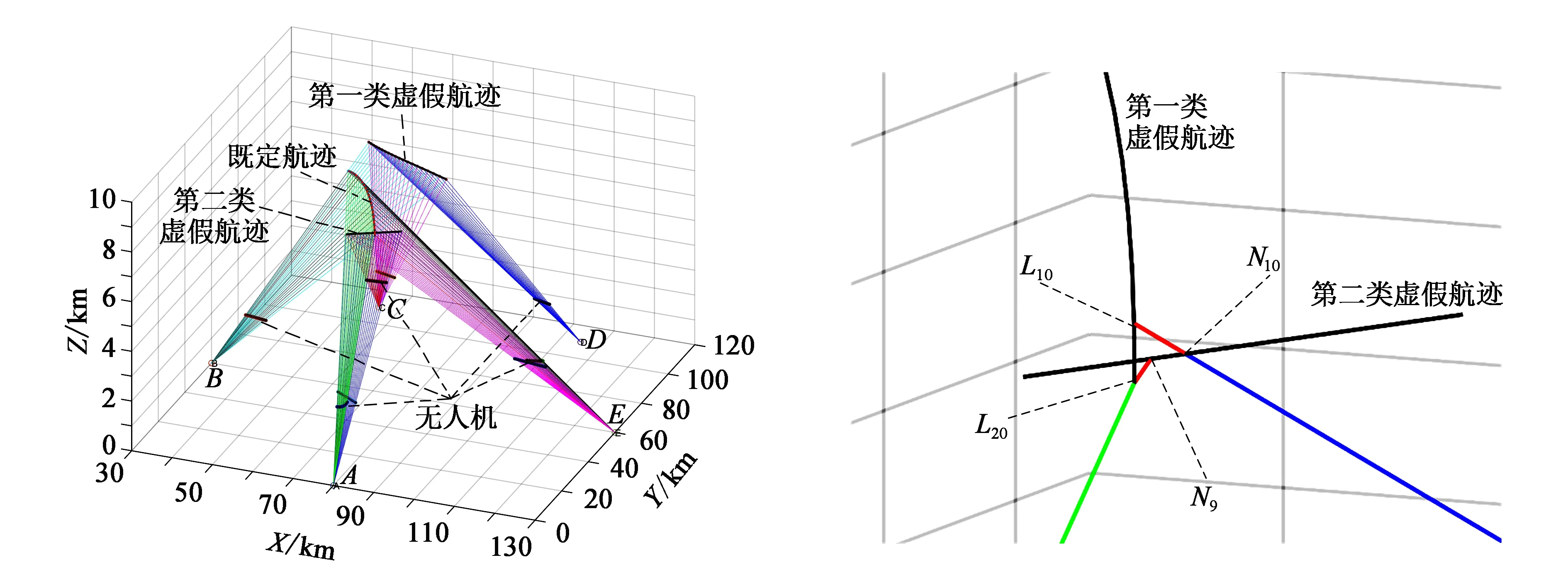
图3 两类虚假航迹的空间分布 图4 第二类航迹耦合处的局部放大图
4 结束语
本文在目前对于一条航迹构造研究的基础上进行研究,从解析几何的角度针对组网雷达的同源检验和数据融合进行分析,对虚假航迹进行分类构造,将虚假航迹构造流程化,在一定数量的无人机编队协同干扰下,对于已有一条航迹额外构造多条虚假航迹,强化了无人机编队的协同干扰效果,对于电子对抗的未来研究具有一定的积极意义。
