基于遗传-鲸鱼优化的SCARA自适应迭代学习控制

马泽楠， 张长胜， 殷淑静， 陈标发

(1.昆明理工大学 信息工程与自动化学院， 云南 昆明 650500；2.西安工业大学 光电工程学院， 陕西 西安 710021；3.广州科伺智能科技有限公司， 广东 广州 510000)

选择顺应性装配机器手臂(Selective Compliance Assembly Robot Arm，SCARA)构造简易，灵活性好，定位运动精度高，主要用于码垛、装配、搬运等快速取放作业领域[1]。机械臂在运动过程中，按照期望轨迹进行重复性位移。机械臂控制系统的不确定性及外界干扰，导致机械臂在重复运动后的实际轨迹与期望轨迹出现偏差，影响作业精度。因此对机械臂关节的位置、速度跟踪误差进行快速精确地控制非常重要[2-5]。

国内外学者针对机械臂控制器参数KP、KD寻优方法的深入研究，提出了不同的策略。文献[6]通过在闭环PD型迭代学习控制算法中引入动态扩张-收缩因子，解决了收敛速度慢且收敛精度不高的问题。文献[7]采用改进的PD控制算法，使用遗忘因子改进收敛条件，得到的误差跟踪曲线更平滑，在迭代误差跟踪方面具有一定的优越性，相比于一般算法更具有效性。针对二自由度SCARA机器人位置跟踪控制，文献[8]设计了基于端口受控哈密顿与反步法的协调控制方案，有效地结合两者的优点，使系统的动态性能和稳态性能良好且抑制干扰的能力较强。文献[9]利用神经网络辨识后的动力学模型，对机械臂进行单神经元PID控制，改进的自适应神经网络PID控制相较于传统方法提高了收敛速度与精度，对目标偏移量的跟踪速度更快。文献[10]中的机械臂在未知环境下对其采用了一种鲁棒自适应迭代学习控制算法，该方法使机械臂的跟踪性能有了明显地改善，收敛速度有一定程度的提升，具有较高的控制精度。文献[11]针对机器人末端位置跟踪误差较大的问题，提出了一种PD滑模控制方法，根据偏差的大小动态地调整增益参数，进而减小外界扰动的影响。文献[12]在机械臂运动时将重力参数加入自适应项中，给出了一种优化后的PD控制方式，提高了机械臂运动时的轨迹精度。

本文针对一般的迭代学习控制算法会受到学习参数的影响，从而使系统收敛性和收敛速度达不到理想要求，降低生产效率，提出基于鲸鱼优化的自适应迭代学习算法，并在鲸鱼算法中引入遗传算法，把两者各自的优势相结合，应用于机械臂控制器参数KP、KD寻优中，以期能提高寻优的全局性，使系统跟踪达到较好效果。

1 SCARA动力学

根据n连杆的动力学模型，得到SCARA的动力学方程：

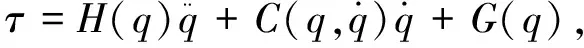
(1)

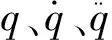
将SCARA机器人简化为双关节的机械臂，把末端负载与小臂视为一个整体，只计算大臂和小臂，模型如图1所示。

(a) SCARA实物

(b) SCARA双关节简化模型

根据Lagrange法得出动力学方程：

(2)

由上式可得控制力矩驱动方程：

(3)

(4)

式中I表示连杆的质心情况，m为杆的质量，l表示应力臂的长度，lc表示应力臂质心位置，θ表示应力臂转角。

式(1)—式(4)可以写成统一形式：

(5)

式中M(qk(t))∈Rn×n为机器人的惯性矩阵，下标k∈Z+表示迭代次数，t∈[0，T]为时间，τk(t)∈Rn表示控制力矩，dk(t)∈Rn表示系统扰动。

2 SCARA自适应迭代学习控制

设计如下控制律：

(6)

(7)

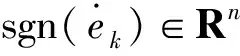
根据式(6)可得，控制力矩的前两项为PD反馈项，第三项为迭代项且系数δk依据上次迭代系数与本次跟踪误差变化而变化，体现出该算法的“学习”特性。

机器人系统参数为[13]m1=m2=1 kg，l1=l2=0.5 m，lc1=lc2=0.25 m，I1=I2=0.1 kg·m2，g=9.8 m/s2，干扰和系统不确定项总和dk=rank(k)sint，rank(k)是[0，1]内的随机数。

两个关节的指令信号分别是sin(2πt)和cos(2πt)。为了保证机械臂初始输出与指令初值一致，设机械臂的初始状态为x(0)=(0，2π，1，0)T。

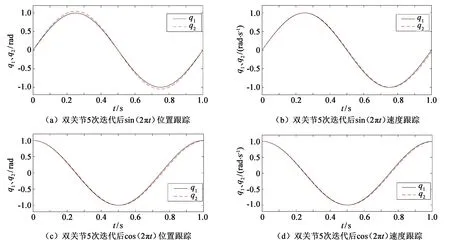
图2 双关节5次迭代后仿真效果

一般情况下，使用实验的方法来整定PID控制器参数，调试过程中的多次尝试是非常重要的，数据如表1所示。在对同一系统不同的KP、KD控制器参数设置的情况下，算法对系统期望轨迹的跟踪效果会出现缺陷。不同参数设置情况下跟踪误差对比曲线图如图3所示。

表1 不同参数设置迭代后的误差数据

通过数据实验，得到在不同的参数设置下，自适应迭代学习控制在前期收敛速度出现了差异，后期收敛精度受到影响。为了使系统跟踪效果达到最佳，要对参数进行寻优操作，找到合适的参数。

3 基于遗传-鲸鱼优化算法的自适应迭代算法

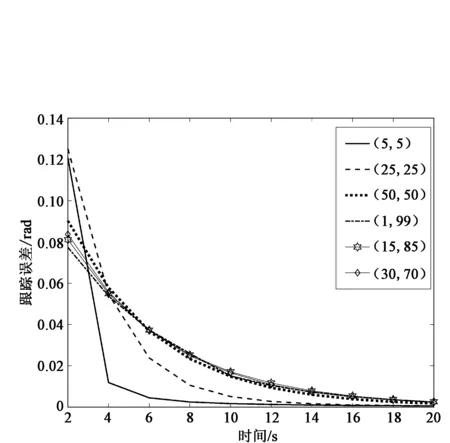
图3 不同参数设置跟踪误差曲线对比图

3.1 基本遗传算法

遗传算法(Genetic Algorithm，GA)通过观察生物界中的选择、遗传机理，对自然进化算法过程进行最优解搜索，属于进化算法(Evolutionary Algorithm，EA)的一种。选择、交叉和变异是遗传算法的3个算子。其中，群体(population)是由一定数量的个体(individual)组成，生物体被称为个体，适应值(fitness)表示对环境的适应度，取决于个体的染色体(chromosome)，用一串数字表示染色体，每一位数字对应一个基因(gene)。新的群体由所有个体进行选择、交叉和变异生成，称作新一代(new generation)。算法流程[14]如下：

步骤一 对初始种群、交叉率、变异率等参数进行初始化；

步骤二 对种群此时的每个待解个体的适应度进行计算；

步骤三 将待解个体在适应度条件下进行筛选或通过交叉变异产生新一代个体；

步骤四 再对父代个体采用均匀交叉、单点交叉等方法，产生新候选个体；

步骤五 对部分个体的基因值通过变异概率方法改变其值；

步骤六 判断当前值是否满足条件，满足退出，不满足返回步骤二。

3.2 基本鲸鱼算法

鲸鱼算法(Whale Optimization Algoritm，WOA)受自然界中鲸鱼捕食过程启发，主要有环绕式捕食、泡泡网捕食和搜索捕食3个阶段[15]。

3.2.1 环绕式捕食

算法中的个体是每一只鲸鱼，算法的解是每个个体在搜索空间的位置。通过回声定位鲸鱼能够识别到猎物的位置，然后对猎物进行围猎，根据公式(8)对个体的位置进行更新：

(8)

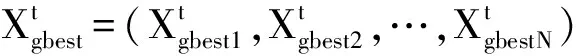
A=2a·rand1-a，

(9)

C=a·rand2，

(10)

其中rand1和rand2为[0，1]范围内均匀分布产生的随机数，a为收敛因子，随迭代次数t从2线性减小到0，即

a=2-2t/tmax，

(11)

图4 鲸鱼的泡泡网捕食行为图

式中tmax为最大迭代次数。

3.2.2 泡泡网捕食

鲸鱼是以螺旋式向上运动并不断收缩包围圈来攻击猎物。鲸鱼泡泡网捕食行为如图4所示。

根据式(9)中收敛因子a的减小实现对猎物进行收缩包围与系数向量A的波动范围的缩小相关。在进行迭代时，收敛因子a从2减小到0时，系数向量A的波动范围为[-a，a]。系数向量A随机地在[-1，1]内产生，个体在t+1时刻的位置始终在收缩范围内，可以是t时刻的位置和t时刻全局最优位置之间的任意位置，在捕食时，鲸鱼根据公式(12)以螺旋运动向猎物游动更新位置，数学表达式如下：

(12)

自然界中的鲸鱼以螺旋形运动逐步向猎物逼近，对此行为进行模拟时，均假设选择收缩包围机制和螺旋更新位置概率为0.5，此过程由公式(13)表示：

(13)

式中p为[0，1]范围内均匀分布产生的随机数。

3.2.3 搜索捕食

鲸鱼如果在收缩包围圈外游动时，此时系数向量|A|>1，个体根据相互位置进行随机搜索，此过程由公式(14)表示：

(14)

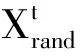
WOA算法的全局搜索和局部开发能力主要受算法中的系数向量参数A的影响，同时参数A的值也取决于a的变化。当|A|>1时，为WOA算法的全局搜索能力，此时种群搜索范围增大，以找到更好的候选解；当|A|≤1时，为WOA算法的局部开发能力，此时种群搜索范围减小，在小范围内进行精细搜索。收敛因子a较大时，算法具有较好的全局搜索能力，能有效改善易陷入局部最优的缺点；收敛因子a较小时，算法具有较强的局部搜索能力，提高了算法的收敛速度。

3.3 遗传-鲸鱼(GA-WOA)优化算法

由于鲸鱼算法在控制参数寻优时会出现实际的优化搜索过程不能完全体现，导致容易使全局搜索与局部开发能力难以控制，在迭代后期种群的多样缺失，个体都开始向局部最优聚集。因此，将遗传算法与鲸鱼算法各自擅长的寻优能力组合，提升算法的收敛效果，算法流程如下：

(1)对候选解群、迭代次数t进行初始化，设置GA和WOA的初始阈值r，当前迭代次数t=0；

(2)根据(KP，KD)初始连接对改进的鲸鱼算法采用初始编码；

(3)以误差为适应度值进行选择、交叉、变异、泡泡网捕食等操作，直至达到条件；

(4)获得最优权值和阈值；

(5)计算误差更新权值和阈值，输出误差结果。

由于PID控制器的参数整定本质是多维函数的优化问题，而鲸鱼算法所采用的编码方式为实数编码，对于自适应迭代学习控制算法中的PD参数直接进行编码(KP，KD)：

X={KP，KD}。

(15)

自适应迭代学习控制算法增益参数优化目标就是使误差趋近于零，这样系统有较快的响应速度和较低的超调量。因此将误差的绝对值和时间的积分作为目标函数：

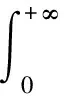
(16)

式中e(t)表示实际输出与期望输出的误差，t为时间。当自适应迭代算法进行20次的迭代之后，鲸鱼算法对自适应迭代算法中的增益参数进行一次更新，用于后续的迭代控制，这样当找到最佳组合值时，停止搜索。

4 仿真实验

基于遗传-鲸鱼优化算法的自适应迭代学习控制算法仿真的实验系统架构如图5所示，得出仿真结果如图6所示，并对结果进行分析。

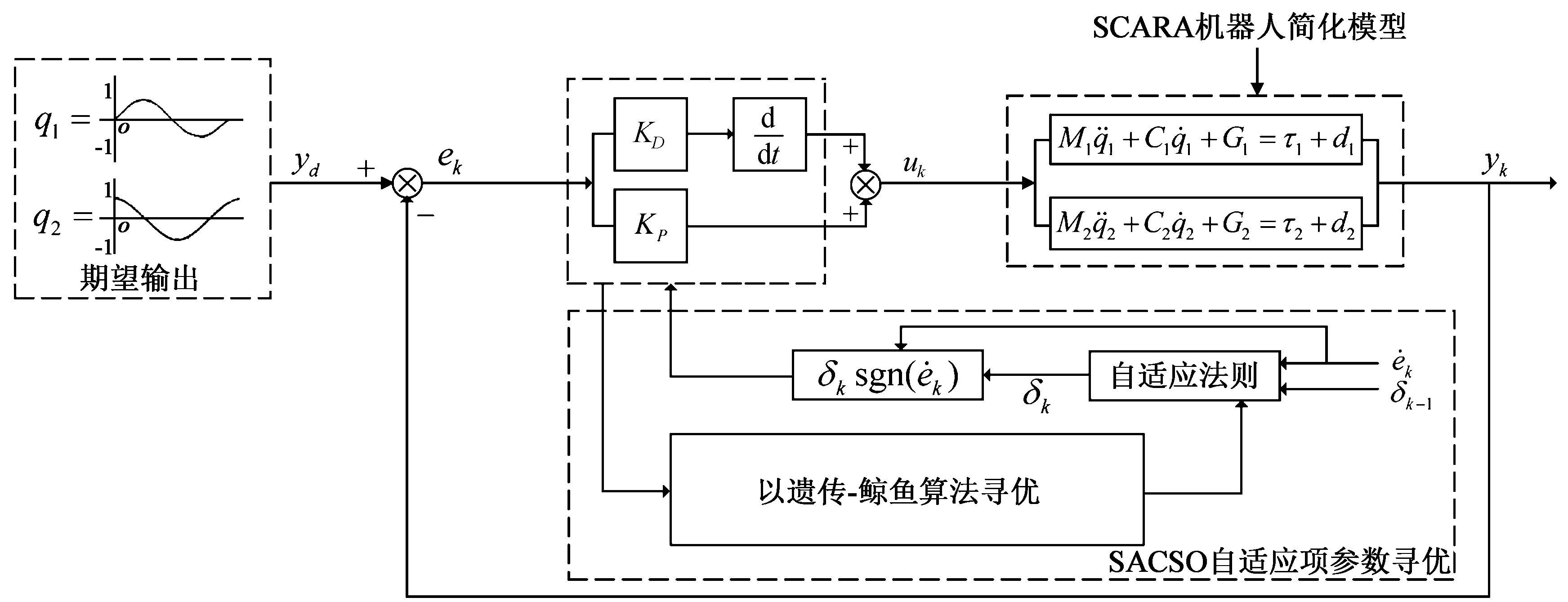
图5 实验系统架构

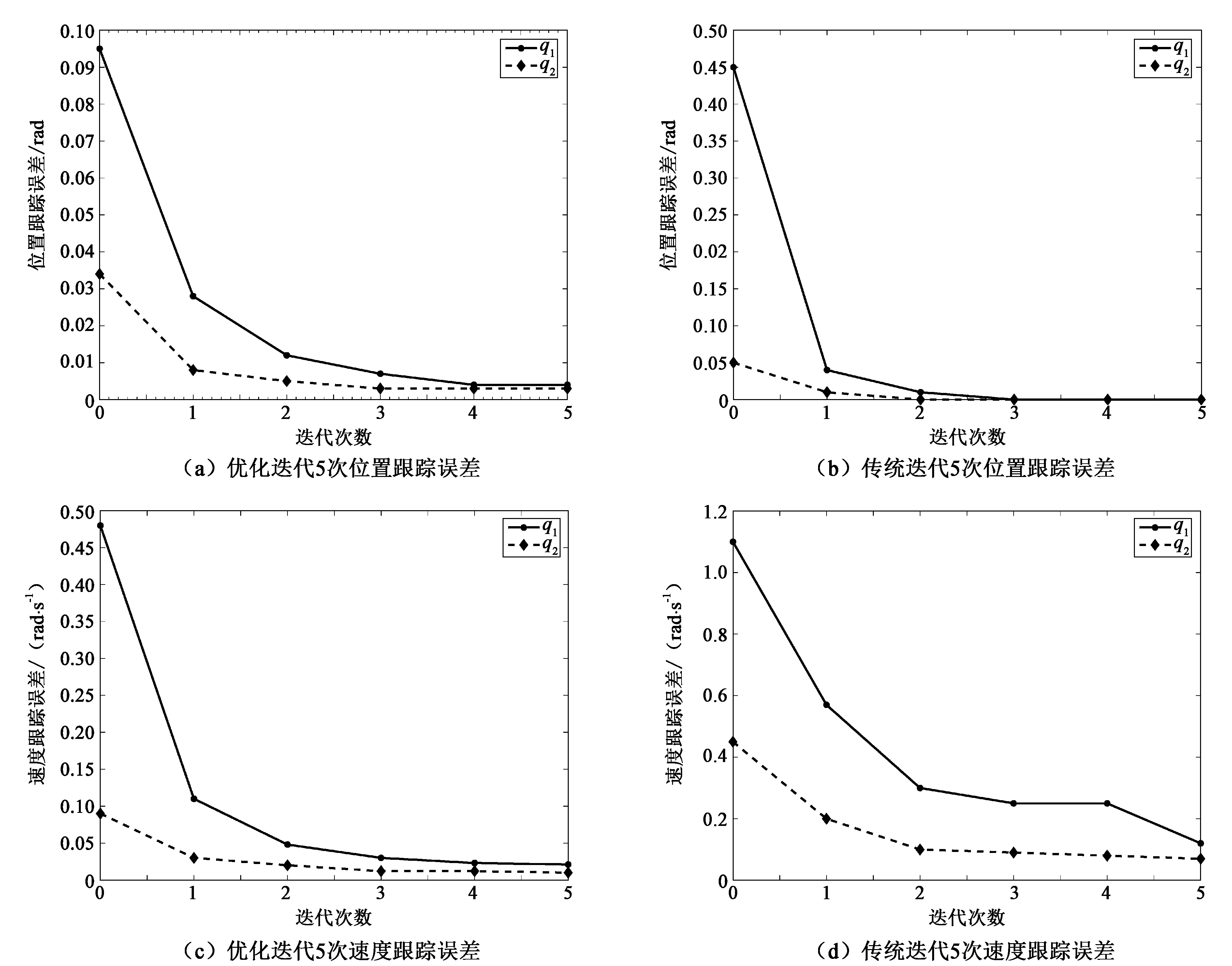
图6 仿真结果

由图6(a)、(b)可知，在关节1和关节2的位置误差跟踪上，基于GA-WOA算法的自适应迭代学习控制在第1次时就收敛到期望值，而WOA算法的自适应迭代学习控制需要约2次；由图6(c)、(d)可知，在关节1和关节2的速度跟踪误差上，基于GA-WOA算法的自适应迭代学习控制在第1次分别收敛到0.11和0.03，而WOA算法的自适应迭代学习控制在第1次时针对关节1和关节2的速度跟踪误差分别为0.58和0.23。因此，在对机械臂控制时，相较于WOA算法的控制，GA-WOA算法的控制对机械臂控制具有收敛速度快、精度高的优势。

为验证算法的有效性设定两组期望轨迹分别为A组：q1=sin(2πt)，q2=cos(2πt)；B组：q1=sin(3πt)，q2=cos(3πt)。按照对SCARA机器人进行的简化分析，将优化后的算法与期望轨迹进行对比，系统跟踪轨迹和误差收敛曲线如图7所示。

图7 系统跟踪轨迹和期望轨迹对比仿真结果

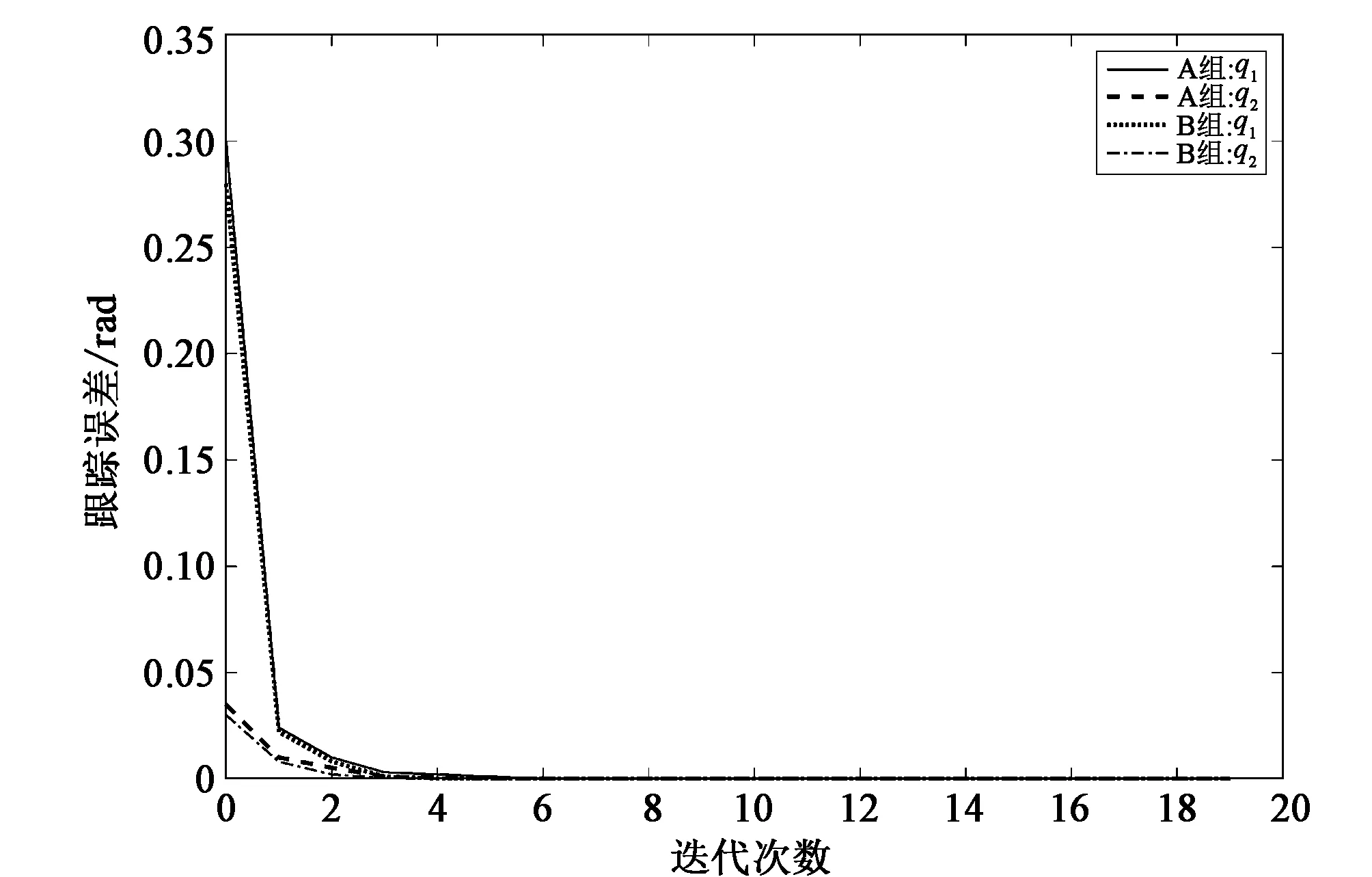
图8 多次迭代跟踪误差

由图7可知，A组与B组轨迹在经过5次迭代以后误差明显减小，对期望轨迹能进行有效跟踪。由图8的结果可以看出，在第1次时系统跟踪误差收敛于期望轨迹，在5次时完全跟踪期望轨迹，验证了基于遗传-鲸鱼优化算法的自适应迭代学习控制算法对改善系统性能具有良好的作用。

5 结 论

本文针对SCARA控制，提出了基于改进鲸鱼算法的自适应迭代学习策略。在鲸鱼算法中引入遗传算法，把GA与WOA各自的优势相结合，提高了寻优的全局性，使系统跟踪达到较好效果。仿真结果分析表明，对控制器参数进行优化后，减少了迭代次数，提高了跟踪误差的收敛速度，证明了GA-WOA算法的自适应迭代学习控制能有效减小执行重复运动任务机器人的跟踪误差，能够对系统期望轨迹进行精确跟踪。