Probability Response of Shape Memory Alloy Beam Subjected to Noise Excitation

,

(School of Science, Xi’an Polytechnic University, Xi’an 710000, China)

Abstract: Shape Memory Alloy (SMA) is a typical material with memory effect, and it is widely used in many engineering fields. Based on the elastic theory and Galerkin method, a vibration system of SMA beam with rigid constraints is proposed. The non-smooth transformation was employed to deal with the discontinuous position, and the original system was turned into an approximate equivalent system associated with the Dirac function. Then, using the stochastic averaging method, the drift and diffusion coefficients of the corresponding Fokker Planck Kolmogorov equation were described. Lastly, the approximate probability response of the system was formulated analytically. Meanwhile, numerical simulation was carried out to verify the effectiveness of analytical results. Furthermore, stochastic bifurcation was discussed. Results show that the stationary probability response of the system was affected by the increase of noise amplitude and restitution force, and a certain restitution value and damping could induce P-bifurcation.

Keywords: Shape Memory Alloy; stochastic averaging; stationary probability density; stochastic bifurcation

1 Introduction

Shape Memory Alloy (SMA) is a special material. Since Greninger and Mooradian[1]observed the shape memory effect on SMA, this material has attracted considerable attention in many scientific fields, such as aerospace[2], aviation[3], and medical application[4]. The characteristic[5-6]and constitutive model[7-8]of SMA were developed in the early 20thcentury. Subsequently, voluminous literature has focused on the analysis of the solution to SMA model in determinative cases. For an SMA actuator, the analysis results have been proposed[9], which were applied to the field of mechanical design[10]. In view of the two-point distribution technique, the exact solution to SMA’s heat exchanger was received[11].

In stochastic cases,the research of probability response is an important topic for nonlinear dynamical systems. In recent years, many methods[12-14]have been developed to solve the problem of probability response, including stochastic averaging method, equivalent nonlinear method[15], and Monte Carlo method. In Ref. [16], super-elastic system’s response under white noise excitation was predicted by the Monte Carlo method. However, the Monte Carlo method involves huge amount of computation and complex algorithms. The stochastic averaging method is a powerful approximate technique for the prediction of probability response. Feng[17-18]applied stochastic averaging method to explore the response of Duffing oscillator under white noise. Bifurcation phenomenon is one of the focus topics in dynamical system. In the nonlinear vibro-impact system[19]and SMA system[20], the stochastic averaging method is applied to analyze bifurcation.

Non-smooth factors are widely existent in engineering fields. In previous literature, the methods of non-smooth transformation and stochastic averaging method were rarely studied for the SMA beam model. Thus, this paper focuses on discussing the probability response and bifurcation for the SMA beam model using stochastic averaging method. Section 2 introduces the SMA beam model with rigid constraint. In view of the non-smooth transformation, the stochastic averaging method is carried out to obtain the average Fokker Planck Kolmogorov (FPK) equation in Section 3. Section 4 shows the numerical results to verify the analytical results. Moreover, the critical values of stochastic bifurcation are investigated in detail.

2 Shape Memory Alloy Beam Model

Consider the model of SMA beam[21]with constraint in Fig.1.l,h,brepresent the length, thickness, and width of the beam, respectively. The model is excited by

F=s0+sζ(t)

(1)

wheres0represents generalized displacement at the initial moment,ζ(t) is the standard Gaussian white noise, andtis time.ζ(t) satisfies

E[ζ(t)]=0

E[ζ(t+τ)ζ(t)]=δ(τ)

(2)

whereτis the time difference,Eis the mean, andδ(τ) represents Dirac delta function.

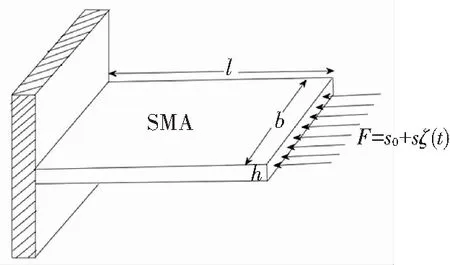
Fig.1 The SMA beam model

The motion equation for the beam is as follows:

(3)

whereMis bending moment of the beam,crepresents linear damping,ωis lateral displacement of the beam, andρAis the mass of the beam per unit length.

Then, the stochastic nonlinear motion equation of SMA beam can be expressed as

(4)

ε0is the symmetric center of the ring, andsrepresents generalized displacement.

Fig.2 shows the sectional view of the model. The dimensionless equation of motion is

(5)

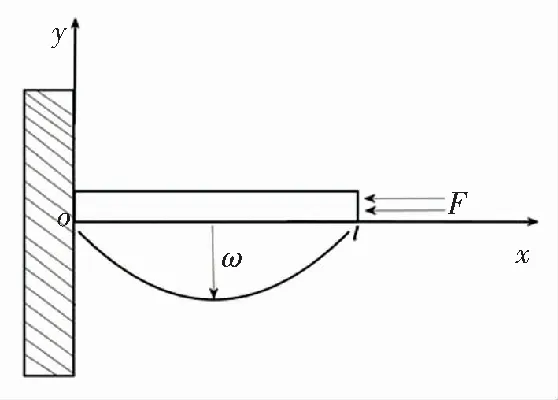
Fig.2Sectionalviewofthebeamwithone-siderigidconstraint

3 Probability Response

Non-smooth transformation is introduced[22-25]:

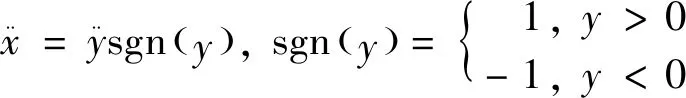
(6)

WithΔ=0 and Eq.(6), Eq.(5) can be rewritten as

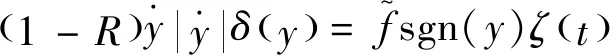
(7)

whereδ(y) is Dirac delta function.

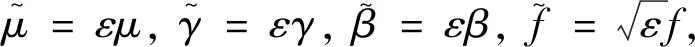
(8)

(9)

in whichW(t) is the Wiener process.

Whenε=0 in Eq.(8), the unperturbed system is obtained. The corresponding energy function and potential function are

(10)

(11)

The derivative of the energy Eq.(10) on the timetis

(12)

(13)

It is known from the Khassminskii theorem[26],y1andy2are two fast mutative processes, andH(t) is a slow mutative process, which is approach to a Markov process asε→0. Therefore, the averaging Itstochastic diffusion process of the Markov process can be described as

dH=〈m(H)〉dt+〈σ(H)〉dW(t)

(14)

whereW(t) is the Wiener process, 〈m(H)〉 and 〈σ(H)〉 are the mean drift and mean diffusion coefficients:

Chasid listened with favour to his servant s suggestion, and perceiving in the valley beneath them a ruin which seemed to promise shelter they flew towards it

(15)

(16)

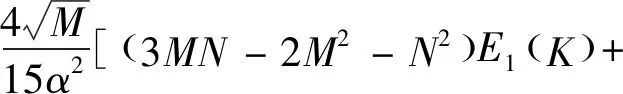
2(M2+N2-2MN)E2(K)]

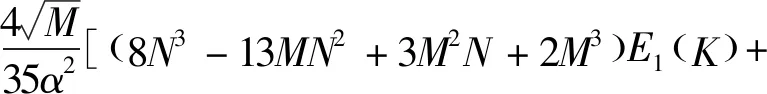
2(-8N3+12MN2-2M2N-M3)E2(K)]

whereE1(K),E2(K) are the first and second kind of complete elliptic integrals, respectively, and

whereAis the positive root of equationU(A)=H. Thus, combination with Eq.(11) obtains the following equation:

(17)

The average FPK equation of Eq.(14) is

(18)

(19)

Therefore, the steady state solution of slow variableHcan be described as

p(H)=C0exp[-λ(H)]

(20)

where

(21)

andC0is a normalized constant. The joint PDF of Eq.(5) can be obtained as below:

(22)

The edge PDFs are received from Eq.(22):

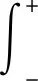
(23)

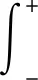
(24)

4 Analysis of Stochastic Response

In this section, the system parameters are taken ask=-1.0,α=0.01,γ=0.01,β=0.01. Based on the original Eq.(5), the numerical results can be obtained by Monte Carlo method. Moreover, stochastic bifurcations is discussed.

4.1 Numerical Simulation

The influence of restitution coefficientRand noise amplitudefon the probability responses of Eq.(5) is considered. Let the parameterμbe 0.01 in this subsection.

As illustrated in Fig.3,it is obvious that analytical results agree with numerical results. When noise amplitude is fixed, the smaller restitution coefficientRcould lead to higher peaks of PDFsp(H), displacementp(x1), and velocityp(x2). In addition, Fig.3(a), (b), and (c) show that the influence of noise amplitudefis similar to restitution coefficientR. These results indicate that the smaller restitution value can make the larger loss of energy, and stochastic perturbation can result in the system’s deviation from the equilibrium position.

4.2 Stochastic Bifurcations

In this subsection, the noise amplitudefis fixed as 0.1. The effect of linear damping coefficientμand restitution coefficientRon PDFs of Eq.(5) were explored.

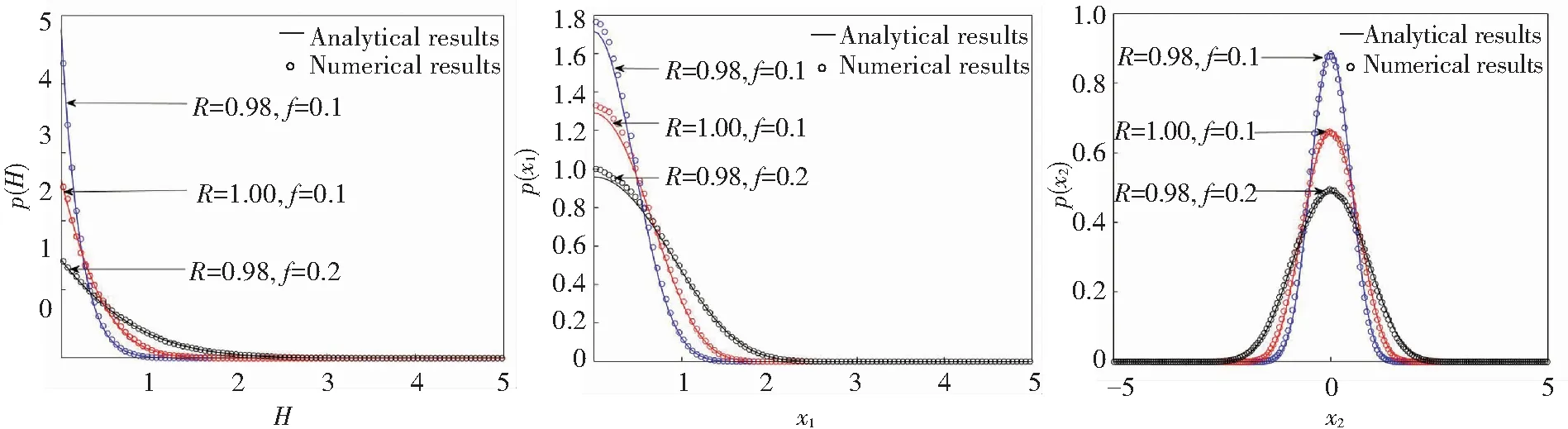
(a)PDF of energy H (b)PDF of displacement x1 (c)PDF of velocity x2

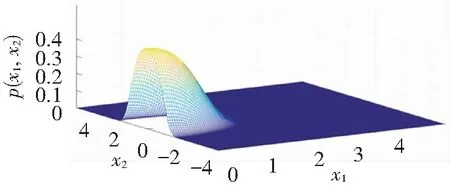
It can be seen from Figs.4-5, analytical results agree well with numerical results whenμ=-0.01. WhenR=0.98, a single peak appears in the joint PDFs as shown in Fig.4. As the restitution coefficientRincreases to 1.0, the join PDFs transits to the shape of crater. This change of PDFs implies that Eq.(5) undergoes a P-bifurcation.

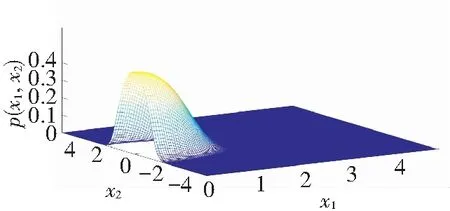
(a) Analytical results

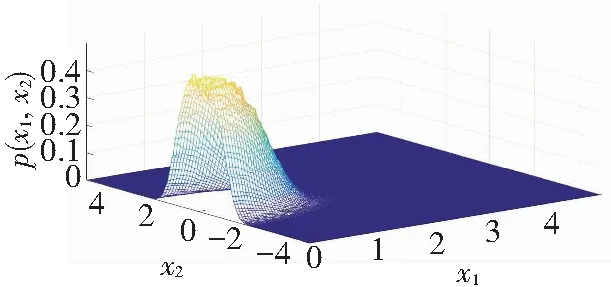
(b) Numerical results

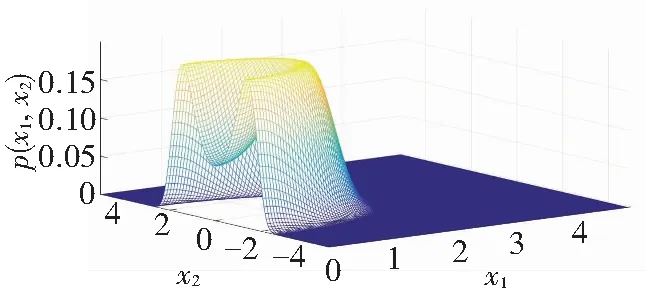
(a) Analytical results

(b) Numerical results

To discover the detailed process of P-bifurcation, the curve of the edge PDFs for different restitution coefficientRis shown in Fig.6.

Obviously, there is only a singular peak forR=0.98. As restitution coefficientRincreases, the curve becomes flatter and eventually turns into a crater forR=1.0. It is can be seen in Fig.6 that the critical value is aboutR≈0.993 during transition. On the other hand, the evolution of edge PDFs implies that a smallerRcan cause a larger loss of energy.

Fig.6TheedgePDFsofEq.(5)fordifferentrestitutioncoefficientR

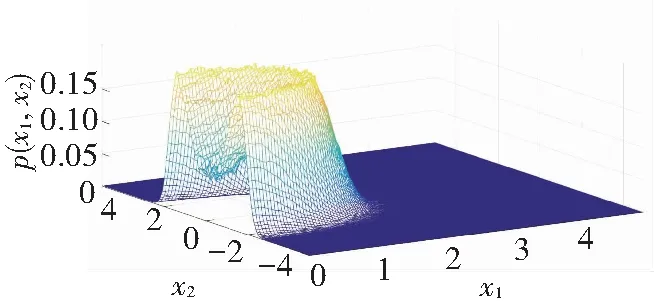
Comparison of Fig.7 and Fig.8 shows that analytical results coincide with numerical results well. Asμdecreases from -0.01 to -0.02, the curve changes from single peak to a crater. The changes indicate the occurrence of P-bifurcation.

(a) Analytical results

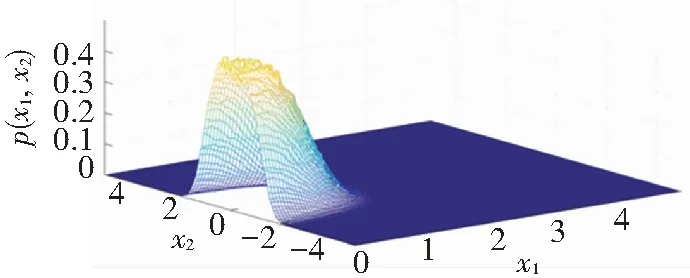
(b) Numerical results

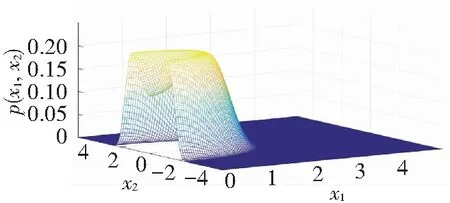
(a) Analytical results

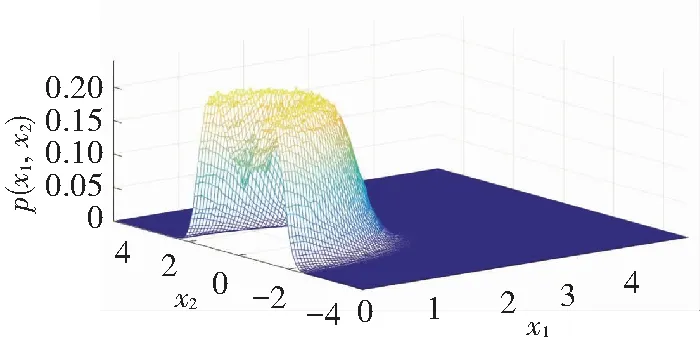
(b) Numerical results

For different linear damping coefficientsμ, Fig.9 describes the procedure of P-bifurcation in detail. It is easy to see one peak occurs forμ=-0.01. Asμdecreases, the curve gets increasingly flatter. Finally, whenμ=-0.02, the form of crater appears. From the evolution of edge PDFs, it was found thatμ≈-0.018 was the critical value that made stochastic bifurcation happen.

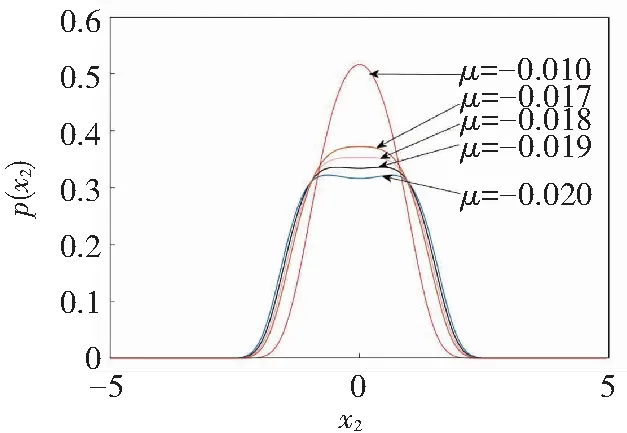
Fig.9TheedgePDFsofEq.(5)fordifferentlineardampingcoefficientsμ

5 Conclusions

In this paper, the probability response of SMA impact model under external Gaussian white noise excitation is investigated. First, the non-smooth transformation was employed to deal with the discontinuous position. Then the original system turned into an approximate system associated with the Dirac function. Lastly, the stochastic response of the approximate system was obtained after analysis. Meanwhile, comparison of analytical results with numerical results demonstrates the effectiveness of the stochastic averaging method. It reveals that the stationary probability response of system is affected by the increase of noise amplitude and restitution force.

Furthermore, this paper explores the P-bifurcation of SMA beam system. It is worth noting that the restitution coefficientRand linear damping coefficientμcan cause P-bifurcation. However, the P-bifurcation usually results in transition of dynamical system, in which unstable vibration is generated and the stability of the SMA beam is destroyed. Therefore, by adjusting the system parameters, the security of the SMA beam could be enhanced.