Vibration Absorption Efficiency and Higher Branches Elimination of Variable-Stiffness Nonlinear Energy Sink

Rui Zhong, Jian’en Chen*, Weimin Ge, Jun Liu and Xiaofeng Wang

(1. Tianjin Key Laboratory of the Design and Intelligent Control of the Advanced Mechatronical System, Tianjin University of Technology,Tianjin 300384, China;2. National Demonstration Center for Experimental Mechanical and Electrical Engineering Education, Tianjin University of Technology, Tianjin 300384, China)

Abstract: Vibration absorption efficiency of a variable-stiffness nonlinear energy sink (NES) was investigated when the main oscillator was subjected to harmonic and impulse excitations. The slow flow equations of the coupled system were derived by using the complexification-averaging method, and the nonlinear equations which describe the steady-state response were obtained. As the harmonic excitation force increased, the system which comprises constant-stiffness NES generated higher branch responses, greatly reducing the vibration absorption efficiency. The influence of nonlinear stiffness on the responses of the system was investigated. Results show that, with the increase of harmonic exciting force, a reduction of NES stiffness can eliminate the higher branch responses and even the frequency band of strongly modulated responses. The vibration absorption efficiency of variable-stiffness NES attached to the linear oscillator for different amplitudes of impulse excitation was investigated. Results show that the proper reduction of nonlinear stiffness under increasing impulse excitation can greatly increase the vibration absorption efficiency of NES, and the variable-stiffness design can effectively mitigate the negative influences of the increase of the excitation amplitude on the efficiency of constant-stiffness NES.

Keywords: nonlinear energy sink; efficiency; variable-stiffness; vibration suppression; higher branch

1 Introduction

In mid-twentieth century, Roberson[1]implemented a vibration absorber with nonlinear stiffness in order to widen its working frequency band and improve its robustness. Until the last two decades, scholars have focused mostly on pure nonlinear absorbers, such as the so-called nonlinear energy sink (NES). NES is an efficient, robust, lightweight absorber that can passively absorb energy over wide frequency ranges[2-3]. Various researches of NES have been carried out, which focused mainly on three areas. The first area aims to study the mechanism and complex phenomenon of target energy transfer (TET). The second area focuses on increasing the efficiency of NES by improving its design. The third aspect is concentrated on the specific application of NES in different main structures and under different excitations.

Lin and Oguamanam[4]pointed out that the efficiency of TET is closely related to the 1∶1 resonance capture, efficiency enhancement is achieved by using strong nonlinearity attachments. Costa et al.[5]investigated the energy transfer between different oscillators. Starosvetsky and Gendelman[6]investigated the mechanism of TET and demonstrated that quasi-periodic beating responses can exhibit more excellent vibration suppression than a steady-state response.

Al-Shudeifat[7]considered a realization of cubic nonlinear stiffness and investigated energy dissipation of NES under shock excitation. Panagopoulos et al.[8]attained efficient TET through choosing appropriate initial conditions. Fang et al.[9]explored a device which comprises an NES and a giant magnetostrictive material to enhance vibration suppression efficiency and realize energy harvesting. Starosvetsky and Gendelman[10]studied the interaction of a linear oscillator attached with an NES with two degrees of freedom. Starosvetsky and Gendelman[11]investigated the efficiency of NES with nonlinear damping under harmonic excitation and found that the utilization of piecewise-quadratic damping can eliminate higher branches. Ahmadabadi et al.[12]presented an optimal design for a system comprising an NES and a piezoelectric-based vibration energy harvester. Main structure with parallel NES devices attached was investigated for absorbing more input energy and improving the efficiency of TET, and the parallel NES devices were found to perform better than single NES[13-14]. Nguyen and Pernot[15]formulated a design criterion to guide optimization of NES parameters. Moreover, in order to overcome the shortcoming of the traditional NES that they can only mitigate excitation in a relatively narrow range of initial energy, a pendulum NES and an asymmetric magnet-based NES were introduced[16-17].

Viguie and Kerschen[18]investigated the dynamics of a nonlinear system coupled with a nonlinear vibration absorber and devised a qualitative tuning methodology for the absorber. Avramov and Gendelman[19]studied the interaction of a beam with a pure nonlinear vibration absorber. Kani et al.[20]studied the vibration absorption efficiency of a beam attached to an NES under external shock excitation, and it was found that, with the increase of the shock amplitude, the optimum value of stiffness of the NES decreases. Research from Guo[21]found that the application of NES on the reduction of whirling vibration amplitude in rotor systems can significantly reduce the resonant amplitude. Zhang et al.[22]used NES to suppress the vibration of composite laminated plate and found that the amplitude of the plate can be rapidly reduced by the NES. The efficiency of NES can also be attained while the absorber is coupled to a multiple-degree-of-system[23]. Lee et al.[24]used NES to suppress the aeroelastic instability in an experiment. Zhang et al.[25]focused on thermal shock-induced vibration suppression of an axially moving beam with an NES. In Ref.[26], NES was placed on a rotating beam to mitigate vibration, and the best range for the parameters of the NES was found as the one in which strong and weak modulated response occur simultaneously. Besides, in Ref.[27], nonlinear approach was proposed for whole-spacecraft vibration reduction. They found that an appropriately designed NES can efficiently absorb and dissipate broadband-frequency energy.

The above researches demonstrated that NES is effective for many kinds of structures. However, excitation energy below a threshold will hinder TET and NES’s activation. Conversely, for too high excitation energy, the dissipation in NES will be greatly reduced. Although NES can absorb energy over wide frequency ranges, the TET in a system can be completed efficiently only within a certain excitation range. The influences of nonlinear stiffness on the energy dissipation of NES have been studied in several papers. However, the relationship between nonlinear stiffness and higher branches of response of a system including NES under large excitation has not been paid much attention to, and the effects of impulse excitation amplitude on the optimum nonlinear stiffness of NES need to be further analyzed. This paper puts forward a variable-stiffness NES scheme, aiming to overcome the reduction of NES performance with the increase of external load.

2 Realization of Variable Stiffness

In Fig. 1, the cubic stiffness is realized by an elastic string with sufficient length and both ends clamped.

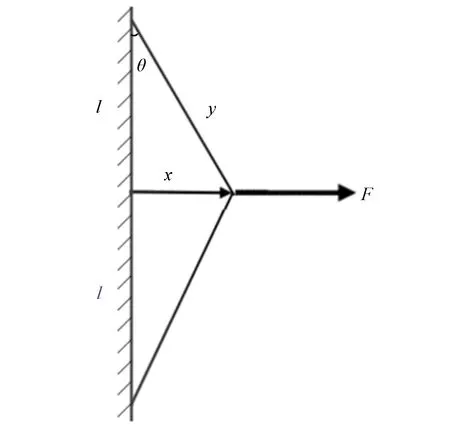
Fig.1 Realization of variable-stiffness

ldenotes the half length of the effective string that clamps between the ends, which can be varied by changing the position of the two ends, andkdenotes the axial equivalent stiffness of the string. ForceFis applied at the middle of the string between the ends. Under the action ofF, each half of the string is stretched to lengthy. The change in length is denoted byΔy, the offset distance from its initial position is marked asx, and the drift angle asθ. The relationship between the force and the change of length can be written as:

F=2kΔysinθ

(1)

Using geometric relations, we obtain:

(2)

Substituting Eq. (2) into Eq. (1):

(3)

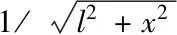
(4)

By neglecting higher order terms, restoring force caused by cubic stiffness can be expressed as:

F≈(k/l2)x3

(5)

This result shows that the cubic stiffness can be adjusted by varying the parameterl, i.e., the effective half length of the string between the two ends.

3 Response Under Harmonic Excitation

The coupled system comprised of a linear oscillator (LO) and an NES with its nonlinear stiffness adjustable is depicted in Fig. 2. Two movable parts below the LO allow the length of the string to become adjustable but do not change the axial equivalent stiffness of the string. The double sided arrows in this figure denote the direction of motion of the movable parts. The equations of motion of the system driven by harmonic excitation are deduced as:

(6)

wherewandvdenote the displacements of the LO and the NES,ωdenotes the linear natural frequency of the LO,γ1andγ2denote the damping coefficients of the LO and the NES, respectively.Adenotes the amplitude of the harmonic excitation,Ωdenotes the frequency of the harmonic excitation,εdenotes the mass ratio between the NES and the LO, and 0<ε≪1. For simplicity,M=1 is chosen for all cases.

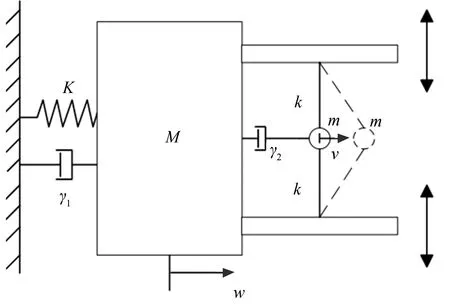
Fig.2 Target energy transfer system

Lettingu=w-v, Eq. (6) can be expressed as:

(7)

We introduce the following transformations:

(8)

whereα1andα2are functions oft, and i is the imaginary unit. Subsequently, we obtain:

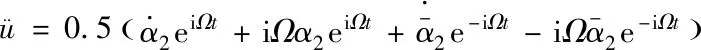
(9)

(10)

Ansatzα1=a1+ib1andα2=a2+ib2are used, wherea1,b1,a2,b2are functions oft. Substituting these into Eq. (10) and separating the real and imaginary part yields:

(11)

(12)

The amplitude of the LO is denoted byAwand it can be calculated using the following expression:

(13)

To determine whether the steady state response of the system is stable or not, let

a1=a10+δ1

(14a)

b1=b10+δ2

(14b)

a2=a2 0+δ3

(14c)

b2=b20+δ4

(14d)

where,a10,b10,a20,b20are the stable solutions of Eq. (11) andδn(n=1, 2, 3, 4) denotes a small disturbance of each stable solution. Taking into account the change of variables (14) and preserving the linear part of the disturbance, Eq. (11) can be rewritten as:

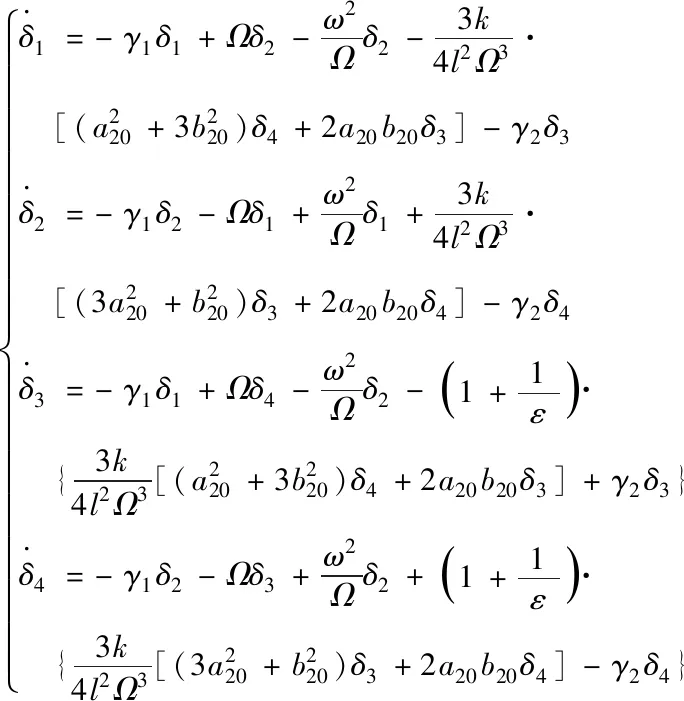
(15)

The characteristic roots of the coefficient matrix of Eq. (15) can determine the stability of the solution, i.e., the solution can be regarded as stable if all the characteristic roots’ real parts are negative.

In this section, the parameters are set toε=0.1,γ1=0.1,γ2=0.2,k=1 500,ω=15, while the frequency of harmonic excitationΩchanges from 10 to 20, the results can be obtained by solving Eq. (12) with Maple solve function. At first, we setl=1, corresponding to NES stiffness ofknl=1 500. To prove the accuracy of the approximation obtained above, numerical results were obtained from Eq. (6) with Runge-Kutta method. When the amplitude of the harmonic forceA=0.4, frequency response of the coupled system can be obtained, as shown in Fig. 3. Results obtained by the complexification-averaging method are pretty close with that obtained by Runge-Kutta method. Fig. 4 shows the frequency response of the LO with and without NES attached, under a harmonic excitation with an amplitudeA=0.4. It can be seen that LO has a stable solution throughout the excitation band and the NES adequately absorbs the vibration energy at this amplitude of excitation.

In Fig.5, we made a further increase of the excitation amplitude, multiple solutions were found by solving Eq. (12) in some specific frequency band. When the excitation amplitudeA=1, as shown in Fig. 5(a), unstable solutions appear in bandΩ=14.8-16.2, which are usually presented as strongly modulated response, and this is beneficial to vibration reduction[28]. However, two new branches appear in the frequency bandΩ=13.0-14.0, i.e., a stable higher branch and an unstable higher branch. In this band, the frequency response of LO may follow the two stable branches according to the accumulation of vibration energy, the vibration of LO stabilizes at the higher branch when enough energy accumulates, which causes its amplitude greatly increases.

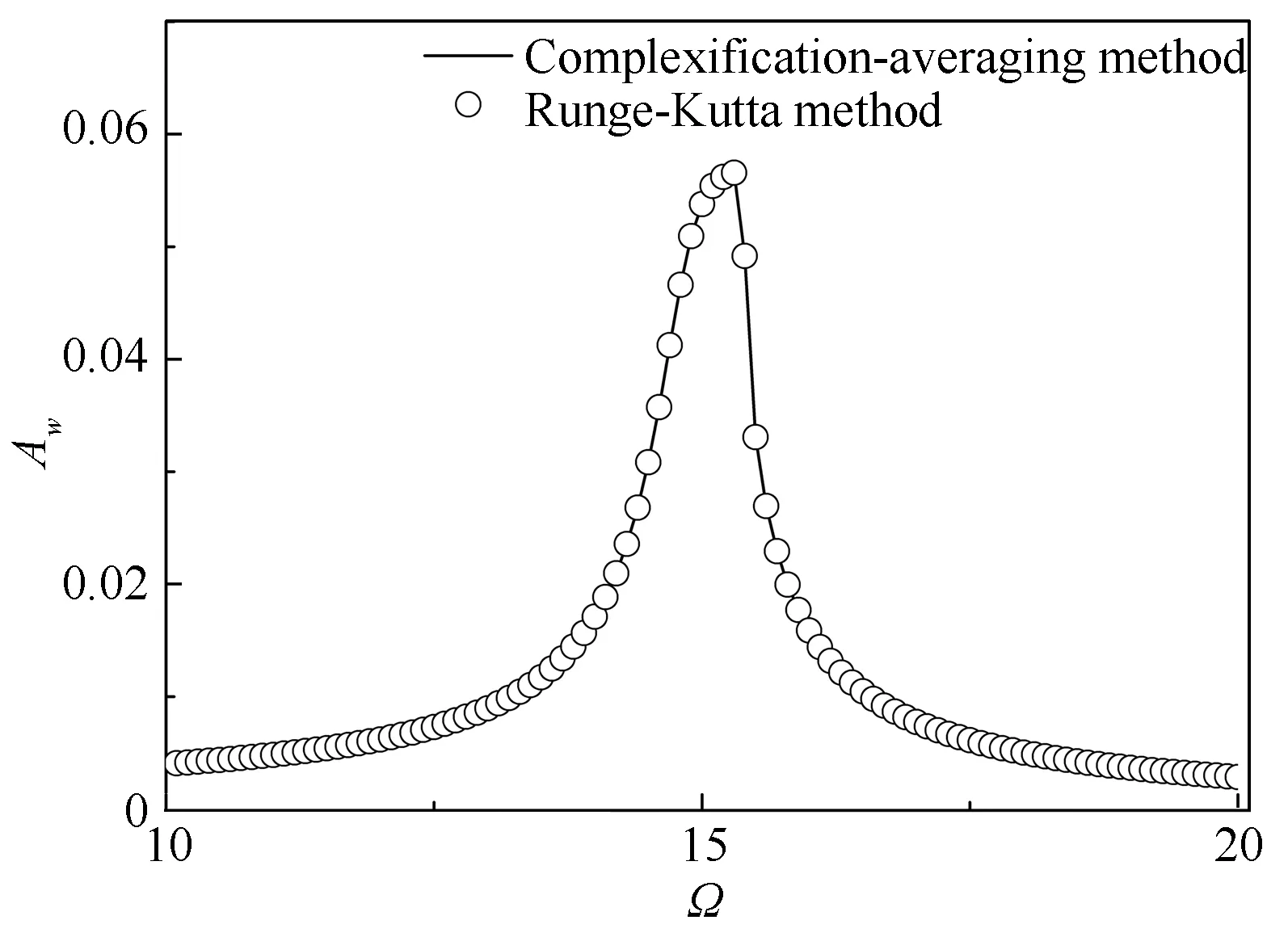
Fig.3 Frequency response of the LO with NES attached for A=0.4

WhenA=3, as shown in Fig. 5(c), the bands of strongly modulated response and the higher branches widen and the amplitude of LO increases. Furthermore, the efficiency of NES under this excitation becomes insufficient. An increase of the amplitude toA=5, as shown in Fig. 5(e), causes the merging of the higher branch and the lower branch,and a single stable solution appears in frequency band

Ω=10-16.3. In addition, the amplitude of LO greatly increases and NES has a negligible effect on the LO, only changing the resonance frequency of the coupled system. The appearance of the higher branches and its merging with the lower branch causes NES to lose its efficacy. To eliminate the higher branches so as to enhance the efficiency of the NES, we varied the parameterl=1.5,l=6.5 andl=9 to suit the amplitude of excitationA=1,A=3 andA=5, and then recalculated the response of the system. As is depicted in Fig. 5(b), Fig. 5(d), and Fig. 5(f), the variable stiffness NES eliminates the higher branches and significantly limits the amplitude of LO, showing good vibration reduction efficiency.

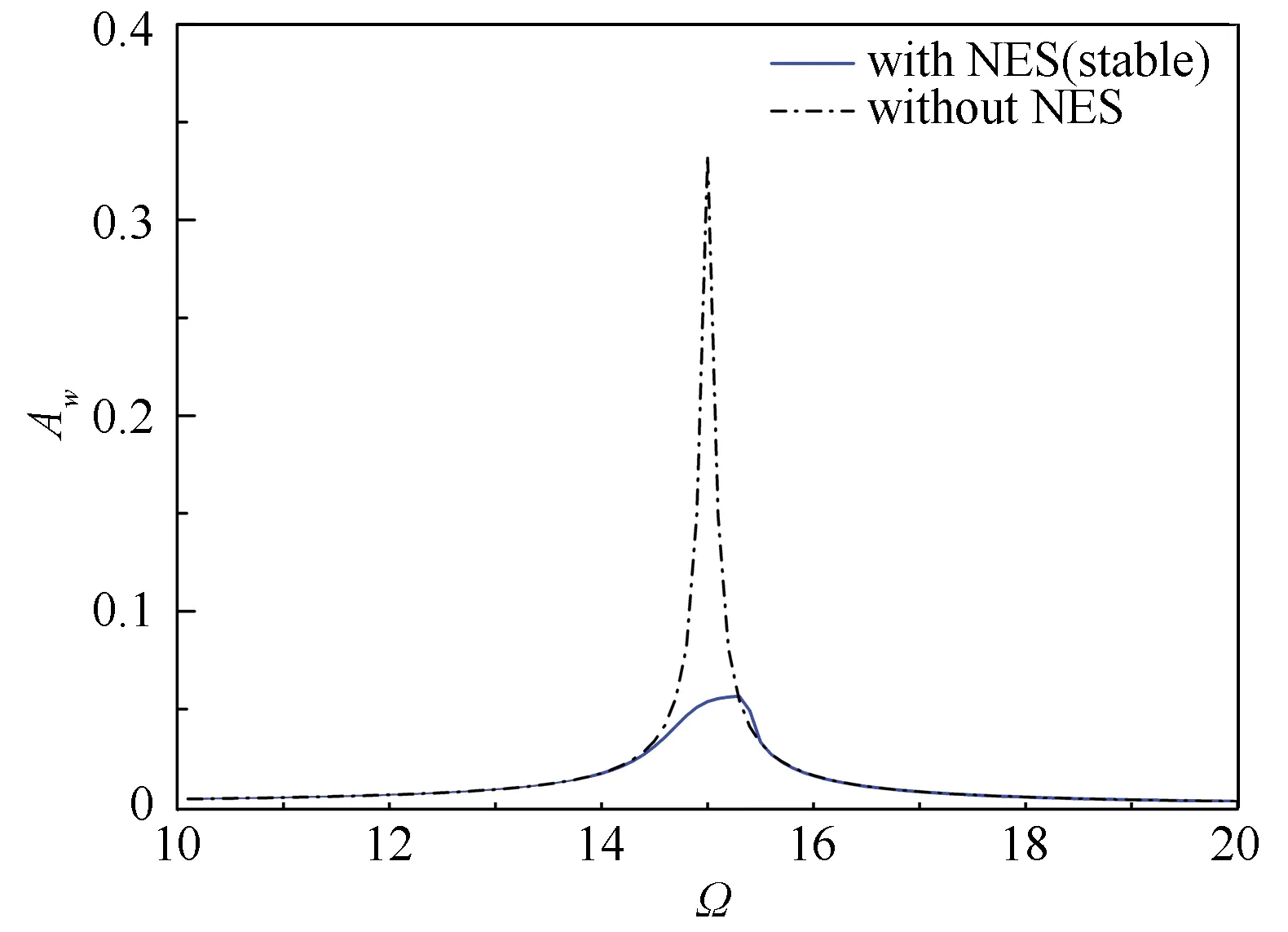
Fig.4 Frequency response of the LO with and without NES attached

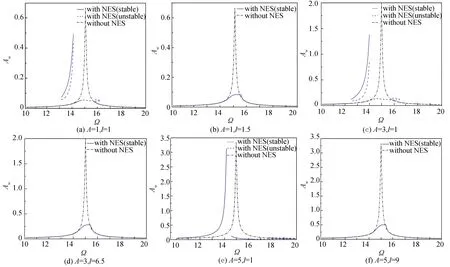
Fig.5 Frequency responses of the coupled system

The frequency band of strongly modulated response of the system under different excitation amplitudes is shown in Fig. 6. As the parameterlincreases, i.e., the nonlinear stiffnessknldecreases, there seems to be no strongly modulated response at first, which is caused by the merging of higher and lower branches. Aslincreases, the higher branch and the lower branch separate, frequency band of strongly modulated response begins to appear and gradually widens. Whenlcontinues to increase, with the elimination of the higher branches, the strongly modulated response band begins to narrow, and finally disappears around the natural frequency of the LO. According to the fact that the band of strongly modulated response is beneficial to the vibration absorption of NES and its widening can also be the sign of the emergence of the higher branch, it is best to maintain that this band exists only near the natural frequency of the LO by adjusting the nonlinear stiffness of the NES for better vibration absorption efficiency.

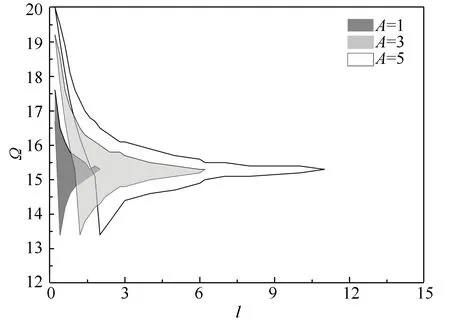
Fig.6 Frequency band of unstable solution of the coupled system

Fig.7 depicts the maximum amplitude of the LO under different excitation amplitudes and for varying NES stiffness parameter. As the parameterlincreases, after a transient fluctuation, the maximum of amplitude of the primary oscillator rapidly decreases to a minimum. Subsequently, the amplitude remains at a relatively low level due to the elimination of the higher branch. However, setting the parameterltoo large would also affect the performance of the NES. It also can be concluded that if the amplitude of excitation changes in a wide range and only constant-stiffness NES can be used, the nonlinear stiffness should be set to a low value in order to enhance efficiency.

Fig.7 Maximum of amplitude of the LO

4 Simulation Under Impulse Excitation

With the purpose of making further investigation of the vibration suppression efficiency of the variable-stiffness NES, we introducedEdiss(t), which denotes the ratio of energy dissipated to the input energy.

(16)

Fig. 9 shows this quantity of the variable stiffness NES as a percentage of the impulse magnitude forA=10 andt=14 s.

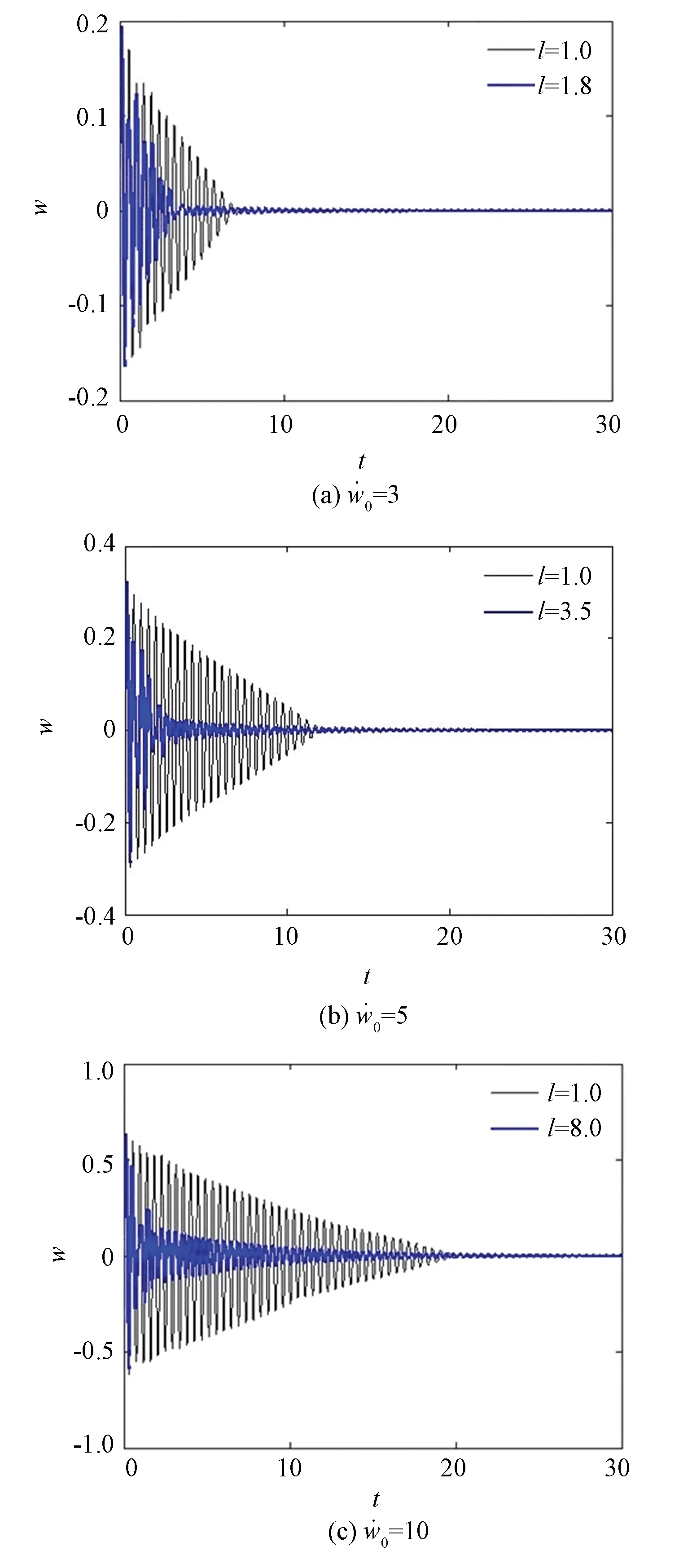
Fig.8 Comparison of the transient response of the coupled system

As the parameterlincreases, the rate of dissipated energy increases rapidly. The absorber performs well forl=4-9, with the ratio reaching up to 90%. If the parameterlis further increased to above 10, the nonlinear stiffness of the absorber becomes small and the efficiency begins to decrease.

However, a satisfactory ratio of energy dissipation (about 70 percent) can still be attained, supporting our harmonic excitation research. In other words, an optimum NES stiffness interval exists for each excitation amplitude, as in the case of vibration absorption efficiency. Prior to this interval (where the stiffness is too high), the performance of NES is unsatisfactory and unstable, and beyond this interval, any decrease of nonlinear stiffness will decrease the efficiency of the NES.

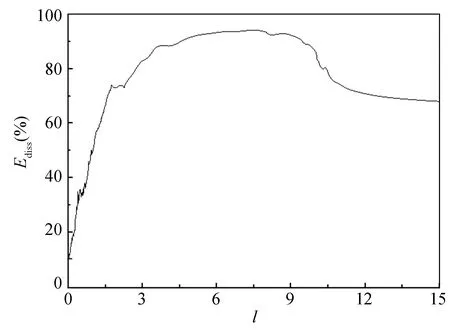
Fig.9 Energy dissipated of the variable-stiffness NES with A=10

Fig.10 Energy dissipated of the variable-stiffness NES vs. impulse magnitude and the parameter of nonlinear stiffness (l)

5 Conclusions

The vibration absorption efficiency of a variable-stiffness NES was investigated in this work. Realization of the variable stiffness was presented. The approximated dynamic equation of the studied system was obtained by complexification-averaging method, after which the stability of the solutions was analyzed. The results show that while the system was under harmonic excitation, increasing excitation amplitude made the system produce the higher and lower branches of the frequency response. These branches merged when the excitation amplitude was further increased, making the NES loses its efficacy. The higher branches can be eliminated and the efficiency of NES enhanced by tuning the parameter of nonlinear stiffness in accordance with the excitation amplitude. Furthermore, while the system was under impulse excitation, the variable-stiffness NES possessed the ability to suppress the amplitude of the primary oscillator and improve energy dissipation efficiency. The results indicate the optimum stiffness of NES is inversely proportional to the amplitude of excitation.

In many fields, especially aeronautics and astronautics, the external excitation amplitude varies widely, and characteristics such as light weight and broadband vibration absorption make NES indispensable. However, the efficiency of constant stiffness NES is influenced by changes in the excitation amplitude. The design of semi-active variable-stiffness systems can make NES well suited for a wide range of applications, and with only a few devices attached. This paper aims to explore a way to enhance the efficiency of the NES under variable loads. The details of the control method of the device were not discussed here. Consequently, the design of semi-active variable-stiffness NES for different primary structures is an open question and of great practical engineering significance.