化归思想方法在偏微分方程求解中的应用

（南昌大学 数学系，江西 南昌 330031）

化归思想方法是指将复杂难解或生疏未知的问题，通过某种转化过程，归结为简单容易或熟悉已知的问题，从而使得原问题得以解决的一种思想方法.偏微分方程理论是预测自然现象变化和解决复杂工程技术问题的有力工具，主要研究偏微分方程定解问题的适定性、解的性质及求解方法等基本理论，成为现代数学中的一门重要分支.偏微分方程常见的求解方法包括特征线方法、行波变换方法、分离变量方法、球平均方法、降维方法、积分变换方法、变量变换方法、幂级数解方法、格林函数方法和数值解方法等[1-5].

化归思想是偏微分方程理论中的重要思想方法，特别是在求偏微分方程的孤立子中具有广泛的应用[6-10].本文以经典的KdV 方程为例，利用化归思想方法求解KdV 方程的孤立子.首先，通过行波变换，将KdV方程转化为一个可积的常微分方程，结合微分方程定性理论，直接求取KdV 方程的孤立波解；其次，通过极限转化，将KdV 方程的周期波解转化为孤立波解；最后，利用数学软件Mathematica 模拟极限转化过程.进一步地，通过此方法可以获得KdV 方程的周期爆破波解和无界波解.

1 KdV 方程的孤立子

利用化归思想方法求取KdV 方程的孤立子，包括行波变换和极限转化等方法，并且通过数值模拟验证极限转化过程.

1.1 行波变换

考虑经典KdV 方程

通过行波变换

其中：c为正常数波速，可将方程（1）转化为常微分方程

对式（3）两边同时关于变量ξ积分，可得

其中：g为积分常数.为了方便起见，不妨令g=0. 作变换φ′=y，则方程（4）可转化为平面系统

根据微分方程定性理论，平面系统（5）是一个具有哈密顿函数

的哈密顿系统.

为得到系统（5）的平面相图，令f(φ)=-3φ2+cφ，则函数f(φ)具有2个零点，分别为φ0=0，.

通过微分方程定性理论可知，(φ0,0)，(φ1,0)分别为系统（5）的鞍点和中心.进一步地，借助数学软件Mathematica 可得到系统（5）的平面相图（见图1）.

图1 系统（5）的平面相图

利用系统（5）的平面相图，结合动力系统分支理论，可得方程（1）的孤立波解.

定理1对于任意给定的正常数c，方程（1）具有孤立波解

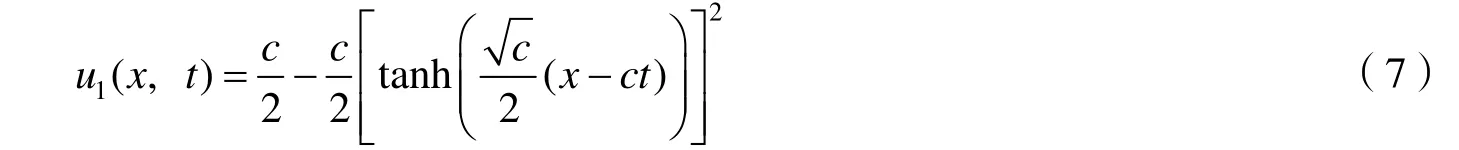
证明由图1 可知，同宿轨Γ1过点(φ0,0)和(φ2,0)，其表达式为

这里φ0＜φ＜φ2.通过对式（9）积分运算，结合行波变换式（2），可以得到方程（1）的孤立波解. 证毕.

1.2 极限转化

由图1 可以看出，当φ5向右趋于φ2时，轨道Γ2逼近轨道Γ1.因此可以通过极限转化获得方程（1）的孤立波解.

求闭轨道Γ2对应方程（1）的周期波解.注意到，过点(φ4,0)，(φ5,0)的闭轨道Γ2与过点(φ3,0)的特殊轨道Γ3具有相同的表达式，即

其中：φ1＜φ5＜φ2，且

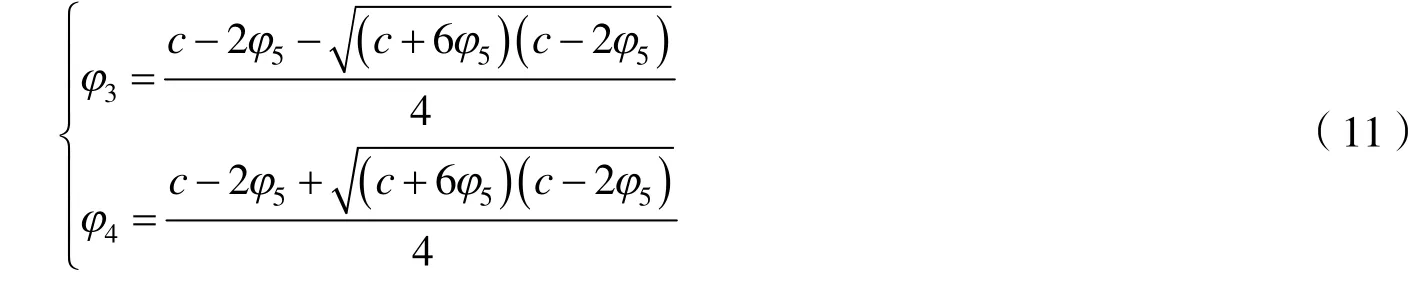
这里φ3＜φ4≤φ＜φ5，对式（12）进行积分变换运算，利用行波变换式（2），得到方程（1）的周期波解

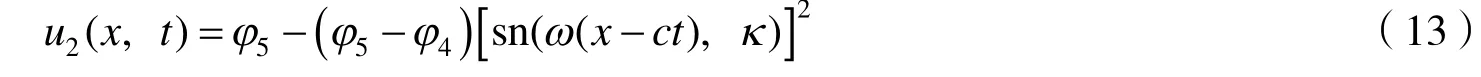
其中

定理2当φ5→0.5c时，方程（1）的周期波解u2(x,t)趋于孤立波解u1(x,t)，即

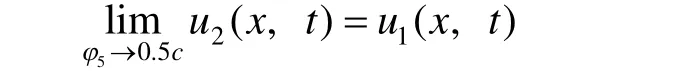
证明由式（11）（13）（14）式可知，当φ5→0.5c时，有φ3→ 0，φ4→ 0，进而

1.3 数值模拟

通过数学软件Mathematica 模拟定理2 中的极限转化过程（见图2），从而验证了定理2 中的理论结果的正确性.

图2 当c=2时，周期波解 u 2(x ,t)趋于孤立波解 u1 (x, t)的极限转化过程

2 方法应用

利用化归思想方法，同理可以解得特殊轨道Γ3，Γ4，Γ5分别对应KdV 方程的周期爆破波解u3(x,t)、无界波解u4(x,t)和周期爆破波解u5(x,t)，其表达式分别为

进一步地，通过极限转化方法，可以得到周期爆破波解u3(x,t)趋于无界波解u4(x,t).证明过程类似于定理2，在此不再赘述.

3 结语

本文通过行波变换方法和极限转化方法等化归思想方法求解了经典KdV 方程的孤立子，并且通过数值模拟验证了极限转化方法的可行性.进一步地，应用此方法获得了经典KdV 方程的其它精确行波解.化归思想方法不仅可以求解经典KdV 方程的孤立子，而且适用于其它波动方程的求解问题，如mKdV 方程的孤立子和Camassa-Holm 方程的尖孤子，以及导出波动方程初值问题的达朗贝尔公式等求解问题，这为偏微分方程课程的教学提供了一些参考.