应用型本科院校高等数学学业成就影响因素研究

（四川旅游学院 旅游文化产业学院，四川 成都 610100）

高等数学作为应用型本科院校一门重要的学科基础课程，其课程教学中的问题也逐渐凸显.学生在学习高等数学的过程中，无法及时地体会到高等数学这门课程对培养逻辑思维和创造意识的重要作用，加之高等数学课程内容逻辑性较强，教学周期长，使学生逐渐产生了畏惧甚至厌恶的情绪，从而导致学生学习高等数学的效果较差[1-2].高等数学学业成就水平的高低不仅直接或间接影响着学生后续课程的学习，而且在促进学生专业素质的提高，拓展学生的综合素质，培养学生的理性思维、应用意识、创造意识、审美意识等方面也起着至关重要的作用[3-6].因此，探讨新形势下学生高等数学学业成就的影响因素，寻求解决问题的对策，对于推进高等数学的教学改革，培养应用型的高素质人才具有重要的现实意义.

学习活动需要智力因素与非智力因素的协同作用才能完成[7].目前提高高等数学学业成就所面临的主要问题是：（1）如何确定智力因素与非智力因素对学业成就的影响力系数；（2）在非智力因素中，确定哪些因素对学业成就的影响力更大.这2个问题的有效解决，有赖于高等数学学业成就影响因素的有效度量，明确高等数学学业成就影响因素的作用机制.基于此，本文根据学生学习高等数学实际情况，将学业成就的影响因素细化为9 个维度，编制出大学生高等数学学业成就影响因素调查问卷，并运用PLS-SEM 模型，实证考察了高等数学学业成就的影响因素及这些因素之间的路径系数及直接与间接作用机制.

1 PLS-SEM 模型原理与方法

1.1 模型原理分析

结构方程模型（Structural equation modeling，简称SEM）整合了因素分析与路径分析2种统计方法，在假设因果关系的基础上，有效地验证模型中的观测变量与潜在变量之间的关系，是一种用以检验某一理论模型适切与否的高级统计技术，在科学研究领域中有着广泛的应用[8].目前，求解结构方程模型主要有2类建模方法[9]：一是由J&o&reskog等学者提出的基于协方差结构的建模方法，即硬性模型，主要以LISREL 方法为代表；二是由Wold 提出的基于偏最小二乘路径的建模方法，即柔性模型，主要以PLS 方法为代表.

1.2 模型建模方法

1.2.1 测量模型 反映性指标的测量方程为

其中：x为外生显变量构成的向量，是ζ的观测指标；y为内生显变量构成的向量，是η的观测指标；λx与λy为因子负荷矩阵；εx与εy为随机误差项.

1.2.2 结构模型 结构模型的方程形式为

其中：η为内生潜变量；ξ为外生潜变量；B为内生潜变量的路径系数矩阵；Γ为外生潜变量的路径系数矩阵；ε为随机误差项.

2 问卷设计与模型研究假设

2.1 样本测试与选取

首先抽样选取四川旅游学院2017 级34 位学生进行调查问卷测试，运用PLS 信效度检验方法对调查问卷进行修正与完善.随后依据修正的学业成就影响因素的调查问卷，采用整群抽样的方法，以四川旅游学院工科类、信息技术类等同时开设高等数学课程的非数学专业2017 级、2018 级学生为研究对象，发放调查问卷.本次调查共发放问卷335 份，回收有效问卷321 份，有效回收率为95.82%.

2.2 潜在变量的指标选择

修正后的高等数学学业成就调查问卷，共计21 个指标题项.采用李克特（Likert）五级量表，分为9个维度，分别为学习压力、数学情感、学习动机、学习态度、数学意志、学习能力、环境调控、教学质量及学业成就.基于问卷设计的适合性确定潜在变量的指标体系（见表1）.

表1 学业成就指标体系

2.3 研究假设

依据潜在变量指标体系，提出研究假设：H1：学习态度对数学意志有直接的正向促进作用；H2：数学意志对学习能力有直接的正向促进作用；H3：数学意志对环境调控有直接的正向促进作用；H4：学习动机对学业成就有直接的正向促进作用；H5：学习压力对数学情感有直接的正向促进作用；H6：数学情感对学习能力有直接的正向促进作用；H7：教学质量对数学情感有直接的正向促进作用；H8：教学质量对学业成就有直接的正向促进作用；H9：学习能力对学业成就有直接的正向促进作用.由此得到结构方程模型（见图1）.

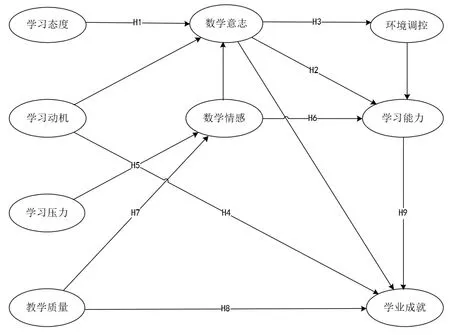
图1 结构方程模型

3 模型实证分析

采用SmartPLS3.2.6 软件的PLS Algorithm 算法，对学业成就影响因素进行测算，得出学业成就路径分析图（见图2）.

图2 路径分析图

3.1 测量模型检验

3.1.1 信度检验 信度检验分为内部一致性信度和组成信度.采用Cronbach′s Alpha 值作为衡量内部一致性信度的指标，以Composite Reliability（CR）值作为衡量组成信度的指标[10].经SmartPLS3.2.6 软件测算（见表2），本模型潜变量的Alpha 值范围是0.712～0.942，均超过0.7，说明本模型的测量指标具有良好信度；所选用的潜在变量的CR 均超过0.7，表明测量指标具有良好的内部一致性.

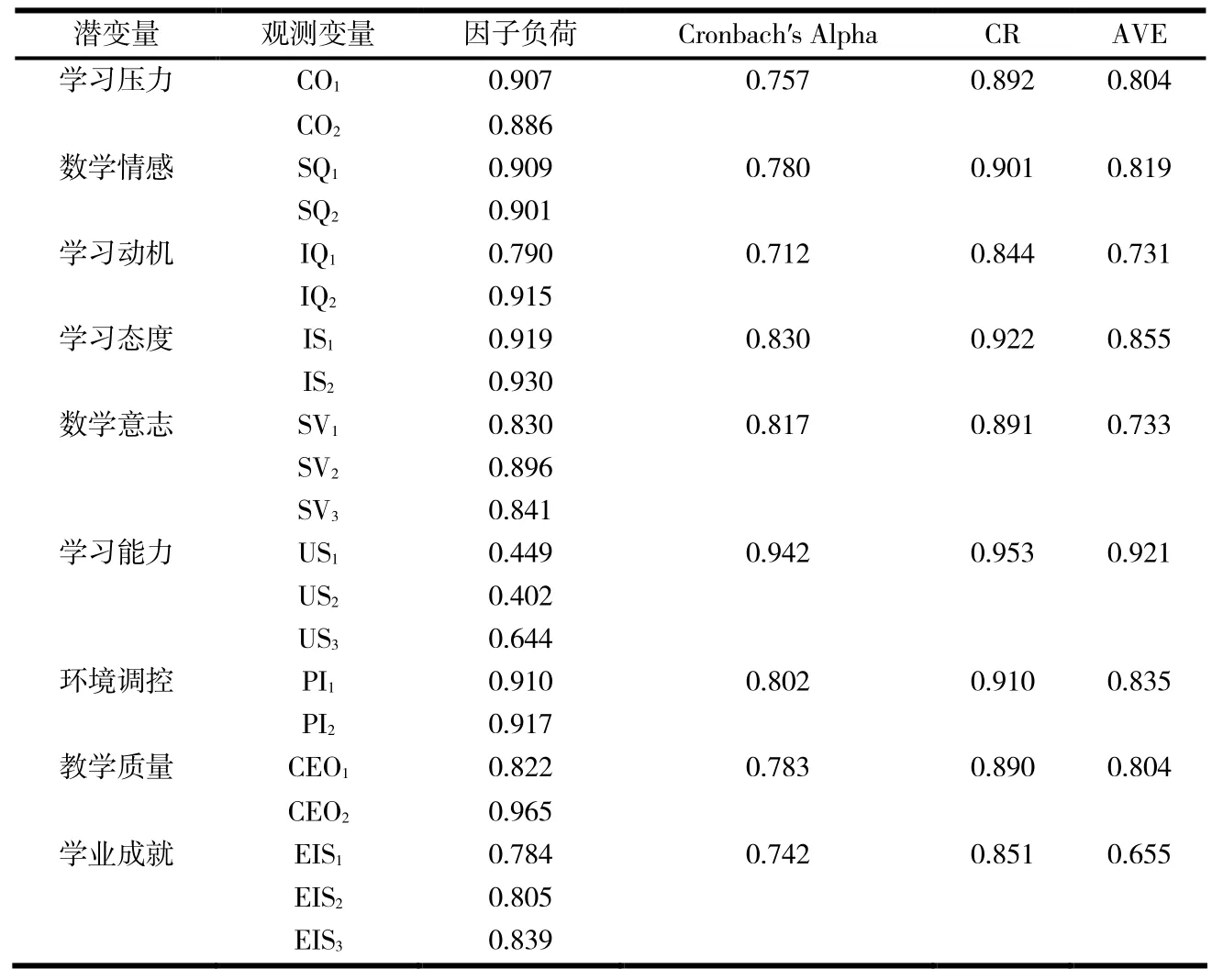
表2 信效度检验结果

3.1.2 区别效度检验 测量模型的区别效度主要用来判别变量之间的差异程度[11]，判别时既要求模型具有良好的收敛效度（AVE 值超过0.5），同时需要模型的AVE 的平方根大于其它潜变量的相关系数.

进行区别效度检验，结果见表3.可以看出，模型具有良好的区别效度.

表3 区别效度检验

3.2 结构模型检验

在SmartPLS3.2.6 环境下，通过PLS Algorithm 及Bootstrap 算法得到的路径系数与统计量t值来检验显著性水平，从而接受或者拒绝原假设.在结构方程模型检验中，当t值大于1.96 时，表示路径系数已达到α值为0.05 的显著性水平，接受原假设，否则拒绝原假设.具体检验结果见表4.

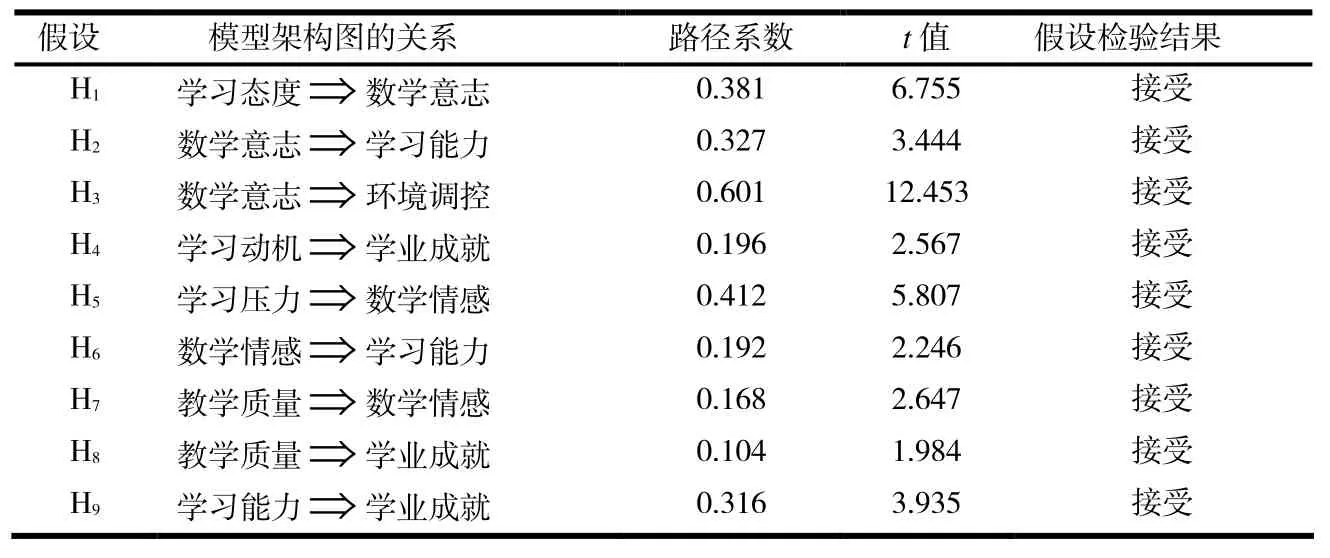
表4 结构模型检验结果

4 结论及教学建议

4.1 结论

（1）对于应用型本科院校的学生来说，学生的学习能力仍是影响学业成就的最主要因素，但不可忽视学生的学习动机与教学质量对学生学业成就的影响.

由表4 可以看出，学习能力、学习动机、教学质量这3个潜变量到学业成就变量的直接路径系数分别为0.316（t=3.935），0.196（t=2.567），0.104（t=1.984），表明路径系数已达到α值为0.05 的显著性水平，故接受原假设.在路径系数中，学习能力对高等数学学业成就的影响力较大，但也不可忽视学习动机及教学质量对学业成就的影响.在教学过程中，教师应注重从专业课入手，引入高等数学的应用价值，特别是以数学建模作为催化剂来激发学生学习动机；同时，教师应从课堂讲授内容改革入手，提高高等数学教学质量，使学生得到更好的学习体验，以此来达到学业成就的进一步提升.

（2）数学意志与数学情感是影响应用型本科院校学生学习能力的重要因素，成为了影响学生学业成就的间接因素.

由图2 和表4 可以看出，数学意志、数学情感对学习能力的直接路径系数分别为0.327（t=3.444），0.192（t=2.246），对学业成就的间接路径系数分别为0.103，0.061.数学意志与数学情感是影响应用型本科院校学生学习能力的重要因素，这2 个重要因素是通过间接方式来对学生学业成就变量达到正向的促进作用.在课程的教学过程中，教师应提高课堂教学的吸引力，并且在教学过程中逐步渗透数学文化与数学思想，加入数学家艰苦卓绝的科学研究过程，强调数学意志力对于学习高等数学课程的重要性；同时，注重培养学生的数学情感，激发数学学习的热情.通过这些形式，可以对学生学习能力及学业成就的提高达到较大的正向促进作用.

（3）学习态度是影响应用型本科院校学生数学意志的直接因素，应在教学活动中适时培养学生积极努力的学习态度.

由于高等数学教学周期长，教学内容较难学习与把控，对于学生的数学意志是一种考验.由表4 可以看出，学习态度对数学意志变量的直接路径系数为0.381（t=6.755），路径系数达到α值为0.05 的显著性水平，接受原假设.由此表明，在较难学习的课程教学过程中，应注重组织优秀学生分享高等数学学习经验，培养学生端正自我的学习态度，从而可以更好地投入到高等数学课程的学习中.

（4）学习压力与教学质量是影响应用型本科院校学生数学情感的重要因素，应重视学习压力与教学质量对学生学业成就的间接影响.

由表4 可以看出，学习压力与教学质量对数学情感变量的路径系数分别为0.412（t=5.807），0.168（t=2.647），路径系数达到α值为0.05 的显著性水平，接受原假设.可以看出，在较难学习的课程教学过程中，应适当提高课程的难度，让学生产生“够一够”才能达到的程度，适当的学习压力对学业成就会产生间接的促进作用；同时，教师应改进上课方式方法，使学生喜欢教师，进而将情感转化为喜欢上一门课程，提高学生学习能力，进而达到高等数学学业成就的提升与进步.

4.2 教学建议

4.2.1 注重激发学生学习的动机 从影响学生学业成就的主要因素出发，注重激发学生学习的动机.虽然学习能力是影响学生学习成就的最重要因素，但是在教师的教学层面上，可以通过激发学生学习兴趣、提高学生自信心等措施来激发学生的学习动机，通过学习动力的正确引导来实现高等数学学业成就的进一步提升.以高等数学教学为例，在教学过程中，基于弗赖登塔尔的“现实、数学化、再创造”的教学理念[12]，采取问题驱动教学法，与学生所学专业相结合.如在讲解函数连续性概念时，针对烹饪、食品专业的学生，以“油温升高的连续性过程”等生活中的实际问题为导向.针对工业设计专业的学生，以“空调温度升高的连续性过程”等生活中的实际问题为导向，设置悬念，激发学生的求知欲；在分析解决问题的过程中，将复杂的问题逐步分解成若干个小问题，通过解决小问题，帮助学生获得成功体验，提高学习的自信心；在问题解决后，设置“对函数连续性、微积分基本公式的理解及其现实意义”等一系列问题，引导学生反思学习过程，进行问题的再创造，达到举一反三的目的；同时设置讨论环节，引导学生分享学习经验，在交流中相互学习，相互促进.

4.2.2 注重渗透数学思想与数学文化 教学中应穿插数学的思想与数学文化，让学生的学习态度与数学意志成为提高学业成就的参考因素.在课程的教学过程中，教师在教学中可以穿插微积分的发展史，介绍牛顿、莱布尼兹、柯西等多位数学巨匠的科学研究过程，逐步渗透数学文化与数学思想，带领学生领略数学家追求真理的精神、艰苦卓绝的科学研究过程，由此使学生体会到学习高等数学的知识需要加入足够的意志力支撑，一蹴而就在高等数学学习过程中是行不通的，从而端正学生的学习态度，激发学生学习数学的热情.

4.2.3 注重培养学生的意志力 意志力是影响学业成就的次要因素，不可忽视学生意志力的培养.在应用型本科院校的课程设置中，高等数学是学生在进入大学后所遇到的第1门课程，学生在学习高等数学课程过程中，大多未及时调整自我，未及时掌握大学课程的学习方法.在教学过程中，教师可以通过帮助学生树立学习目标和学习计划，及时有效教学反馈，注重榜样教育等措施来提高学生的意志力.在学期开始时，教师可以鼓励、帮助学生坚定数学的学习目标，制定每周的学习计划，引导学生阶段性总结学习成果，从而提高学生的学习意志力，也可以组建数学学习互助小组，通过学生的“一对一”或“一对多”帮扶潜移默化增强学习的自觉性.在教学过程中，教师应当引导学生独立思考问题，鼓励学生敢于思考，不要畏惧失败，同时教师要对学生的数学学习给予及时中肯的评价，有效的教学反馈也有助于提高学生的意志力；同时，教师可以对学生进行榜样教育，让学生意志力受到潜移默化的熏陶.

4.2.4 注重培养学生的课堂感知力 教学质量可在一定程度上给学生带来数学情感的不同体验，应重视应用型本科院校学生的课堂感知力.学生对于一门课程的喜爱和兴趣，首先是来自于对任课教师的好感与良好的师生关系，任课教师应随时站在学生的角度，给自身设置疑难问题，以设问的方式引领学生进入学习情境，尽最大努力去创造民主的师生关系与轻松积极的课堂氛围.在讲解函数间断点有关知识过程中，学生在判断是否为可去间断点时，将可去间断点的类型仅局限在“趋近于某点的极限不等于该点的函数值”，而未考虑到函数可能会出现无定义的类型.这时，教师就要加强与学生之间的沟通，了解到底是何种原因造成的困扰，如果是前者，教师可以帮助学生重新梳理函数连续性概念；若是后者，教师可以重新讲解可去间断点的判定法则以达到概念的强化理解；同时，教师应以饱满的热情进行课堂的教学，营造活跃、乐观的教学氛围，让学生对数学产生浓厚的兴趣，鼓励学生大胆想象，积极探究，进而实现高等数学教学质量的提升.