基于离散元与多体动力学的微耕机旋耕刀轴负荷分析

刘妤, 刘羽平, 张拓

(重庆理工大学机械工程学院, 重庆 400054)

随着工业化、城镇化等政策推进，大量农业劳动力向非农产业转移，导致农业生产面临劳动力不足的问题[1]。适宜的土壤耕作技术对于减轻劳动强度、节约能源、增加产量、提高经济效益、保护农业生态环境都有积极的作用[2]。农业机械化是解决劳动力不足的有效路径，微耕机作为我国丘陵山区典型的小型农业机械，解决了大型农业机械无法进场作业的难题，在推动丘陵山区农机化水平方面发挥了积极的作用[3]。微耕机作业时，发动机通过变速箱将动力传递到刀轴，刀轴上的旋耕刀片与土壤相互作用，实现切土、翻土、碎土、平土和前行，可见，旋耕刀辊是微耕机的核心部件，其耕作性能的优劣直接影响微耕机的耕作效率和作业质量[4]。

近年来，主要通过试验、数值模拟方法研究耕作部件作用于土壤的效果。常用的数值方法包括有限元法、光滑粒子法、离散元法等，其中，离散元法应用较为广泛[5-11]，应用于土壤耕作模拟研究更加有效。而在旋耕刀耕作研究方面，方会敏等[11]基于离散元法分析了旋耕刀在有/无秸秆覆盖的土壤中工作时的受力情况，并通过试验验证了仿真分析的有效性，结果显示，旋耕刀在有秸秆覆盖的土壤中所受的阻力总比无秸秆覆盖的土壤中的大。熊平原等[12-13]借助离散元软件平台EDEM对单组旋耕刀三向工作阻力规律进行了模拟研究，与土槽试验结果相比，阻力变化趋势相同，耕深对旋耕刀三向阻力影响显著。Lee等[14]研究了旋耕刀数量、刀刃形状及其对功率和土壤破碎的影响，发现单组旋耕刀数量为4是最佳选择。Chertkiattipol等[15]对比了日本C型刀、欧洲C型刀和L型刀的耕作性能，发现日本C型刀与欧洲刀翻土性能相近，但耕作阻力更小。Matin等[16]研究了三种不同形状的旋耕刀在四种转速下的功率、扭矩，得到了节能使用所对应的转速范围。Li等[17]运用光滑粒子法和试验方法研究了单旋耕刀参数与功率的关系，建立了回归模型。夏俊芳等[18]基于ANSYS/LS-DYNA对螺旋刀辊土壤切削过程进行了模拟，得出了螺旋刀辊切削土壤的功率消耗、切削阻力的大小以及土壤等效应力的变化规律。朱留宪等[19]运用SPH算法对微耕机旋耕切土进行了仿真研究，分析了旋耕刀辊的切土过程，计算得到的微耕机在给定工况下的切土功率与实际使用功率比较接近。

上述研究大多是针对单一旋耕刀片或单组旋耕刀开展研究，而实际的刀辊结构中，同一刀轴上有多组旋耕刀。同时，离散元软件只能模拟土壤颗粒与刀具之间的相互作用，无法模拟刀具和刀轴之间的相互作用，从而无法模拟土壤与多体工具作用的工况，而采用离散元与多体动力学耦合计算分析，能够描述散体物料颗粒与多体工具的作用效果[20]。为此，本文以实际的微耕机刀辊结构为原型，基于离散元法和多体动力学软件平台分析其作业时的等效负荷，以期探讨旋耕刀与土壤的相互作用，为优化微耕机作业性能提供参考。

1 材料与方法

1.1 土槽试验

1.1.1试验指标选取 旋耕刀在进行土壤耕作时经历切削、破碎和抛掷三个过程，此过程中土壤对旋耕刀形成反作用力，即耕作阻力。耕作阻力的大小、方向和作用点与耕作条件(刀轴转速、机器前进速度、耕作深度等)、旋耕部件结构(刀片数量、刀片排布方式等)以及土壤理化特性等有关。旋耕刀轴所受的等效扭矩为各旋耕刀在同一时间受到的耕作负荷的综合作用，因此，本文以刀轴上的扭矩作为试验指标。

1.1.2试验条件 本文所针对的旋耕刀为重庆地区微耕机广泛采用的旱地弯刀。以WM1100D为例，该型微耕机左右对称配置一刀轴，刀轴半径190 mm，单刀轴长425 mm，通常布置3个刀盘，相邻刀盘间距140 mm，每个刀盘上安装有4把旋耕弯刀，如图1所示。

试验在本课题组与农机企业共建的室内土槽试验台(图2)[21]上进行。试验土槽长10 m、宽1.5 m、深0.8 m，旋耕刀刀轴安装在试验车上，试验车由电机驱动，并设计有土壤恢复、耕深调节、压实深度调节等装置。

注：1—刀轴；2—贴应变片处；3—旋耕刀；4—刀盘。Note: 1—Cutter shaft; 2—Poison of strain gauge; 3—Rotary blades; 4—Tool holder.图1 微耕机刀轴Fig.1 Rotary-blades-roller of micro-cultivator

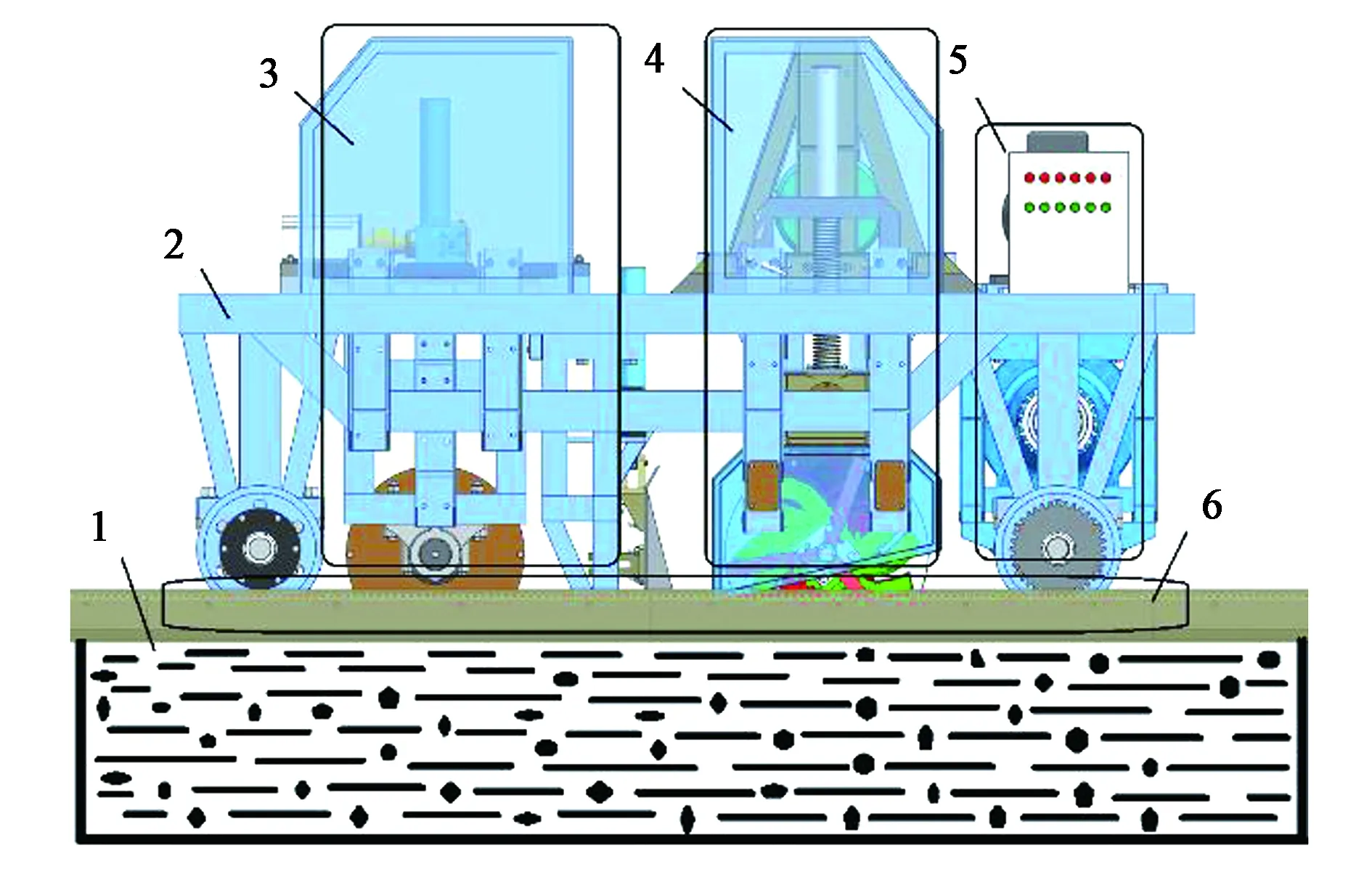
注：1—土槽；2—车体机构；3—土壤恢复系统；4—旋耕系统；5—试验车驱动系统；6—行走轨道。Note: 1—Soil bin; 2—Frame of test car; 3—Recovery system of soil; 4—Rotary tillage system; 5—Drive system of test car; 6— Walking track.图2 土槽试验台结构Fig.2 Structure of soil bin test rig

试验土槽内土壤为重庆地区典型的紫色土，其性质如下：密度1.92 g·cm-3，含水率36.5%，内聚力4.76 kPa，内摩擦角2.72°，坚实度642.72 kPa[22]。

1.1.3试验方案 考虑到刀轴负荷的测试系统不能对微耕机产生结构性破坏，且应具有所需安装空间小、拆装和使用方便等特点，本文采用无线方式(应变片+无线扭矩信号模块)对旋耕刀轴等效扭矩进行测量。其中，选用中航电测股份有限公司的应变片(电阻350 Ω，灵敏度2.09)，以单片全桥的形式布置在靠近刀轴与刀盘焊接处(距离刀盘20 mm)，测量的刀轴为左侧刀辊的刀轴；选用东华DH5905无线扭矩模块采集旋耕刀轴的等效扭矩发送至计算机，并对采集信号进行存储、处理。试验前对动态扭矩测量系统进行标定，结果如式(1)所示，拟合误差为1.2%[23]。

y=6.453 5+0.554 9x

(1)

式中，y为载荷，N·m，x为应变量。

该型微耕机设计的作业耕深为150 mm，但实际耕作中，农户往往使刀轴与耕地表面相平，达到约200 mm耕深。因此，本文着重探讨设计作业耕深、实际作业耕深工况下的刀轴负荷。试验过程中，参数设置如下：试验车行进速度0.2 m·s-1，刀轴转速110 r·min-1，耕深150 、200 mm，而且，尽可能确保每次耕作试验时的土壤状况相近，记录不同工况下刀轴耕作状态下的扭矩值。每次试验时间为20 s，待试验车运行稳定后进行数据采集。

1.2 数值模拟

1.2.1土壤颗粒接触模型 本文所针对的土壤是一种可压缩的粘性土壤，鉴于EEPA(edinburgh elasto-plastic adhesion model)综合一个考虑了弹塑性接触变形的非线性滞回弹簧模型和一个与塑性接触变形函数有关的粘着力分量[24]，能够较好地反映土壤与工具的作用过程，因此，选择EEPA模型建立土壤模型。

EEPA模型中，法向接触力与重叠量之间的关系如图4所示[25]。实际应用时，需设置如下参数：初始接触力f0，用于描述范德华力、静电力等；细观接触表面能Δγ，用于计算黏着力；接触塑性比λ=1-k1/k2，其中k1为初始加载刚度，k2为卸载或重新加载刚度；非线性指数n，用于力与重叠量之间关系的线性、非线性转换；黏着力曲线指数x，用于评估卸载使黏着力下降的程度；切向刚度因子ζtm，用于确定切向刚度。

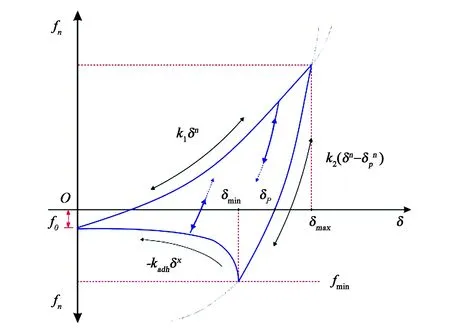
注：fn 为颗粒间法向力，N；δ为颗粒间的法向重叠量，m；f0为颗粒间现存的接触力，如范德华力或静电力等，N； k1 为初始加载刚度， N·m-1；k2为卸载/重新加载刚度，N·m-1；fmax为颗粒间最大粘结力，N；-kadh为粘结力衰减刚度，N·m-1。Note: fn is normal contact force between particles, N; δ is normal overlap between particles, m; f0 is the existing contact force between particles, such as Van Edward force or electrostatic force, N; k1 is intital loading stiffness, N·m-1; k2 is unloading/reloading stiffness, N·m-1; fmax is the maximum adhesion force between particles, N; -kadh is the attenuation stiffness of adhesion force, N·m-1.图3 EEPA模型[24]Fig.3 EEPA model[24]

1.2.2土壤模型参数 土壤颗粒模型材料参数包括剪切模量、泊松比、密度，材料之间的接触参数包括恢复系数、静摩擦系数、动摩擦系数。材料参数可以利用实际材料测得的参数，对模拟结果影响较小，材料之间的接触参数需要进行标定以保证模拟精度。本研究耕作模型材料参数[22]如表1所示，土壤颗粒与旋耕刀及试验土槽模型接触参数[26]如表2所示。标定过程中采用的颗粒半径为3 mm，正态分布，标准差0.07 mm，定义EEPA接触模型中初始接触力、细观接触表面能、接触塑性比、非线性曲线指数、黏着力曲线指数和切向刚度因子分别为-0.01、13、0.7、1.5、5和0.276[27-29]。

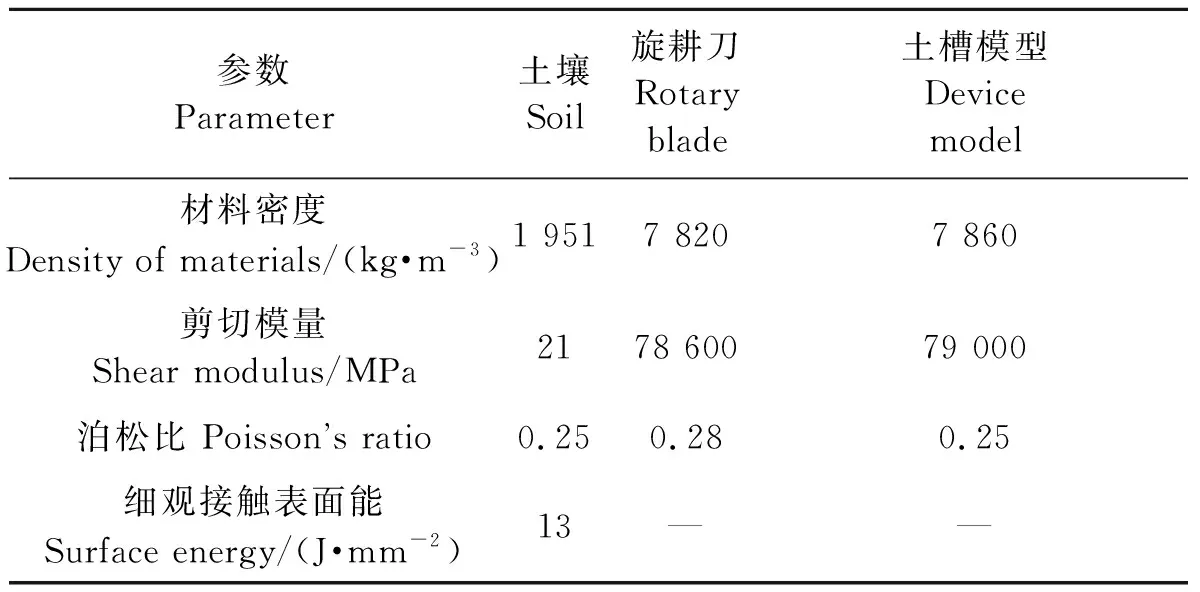
表1 材料性质参数Table 1 Physics parameters of materials

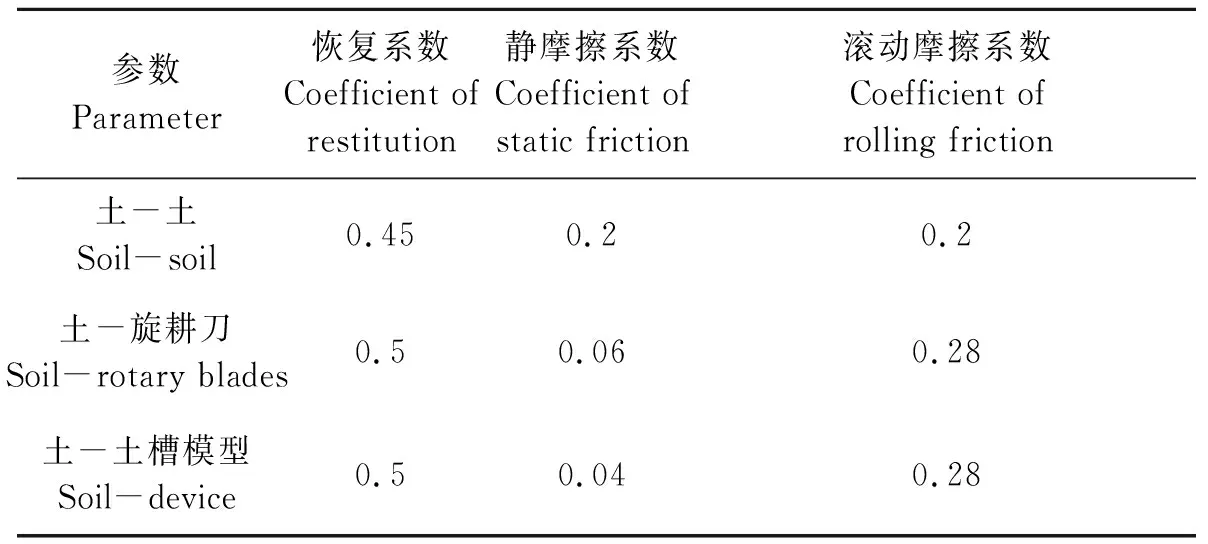
表2 材料接触参数Table 2 Contact parameters between soil and tool materials

1.2.3耕作模型建立 基于EDEM-Recurdyn建立耕作模型对多组旋耕刀耕作过程进行耦合模拟。鉴于微耕机两刀辊对称布置，为减少模拟计算量，只建立单侧刀辊的耕作过程模型，且该刀辊为微耕机耕作前进方向的左侧刀辊，以便于与试验结果对比。具体的建模过程如下：首先，根据表1、表2的参数在软件EDEM 2018中建立土壤模型，根据求解结果中颗粒速度判断颗粒静止后，导出土壤模型(设置导出模型模拟起始时间为0 s)以方便进行不同耕深工况的模拟，避免土壤模型的重复建立；其次，在Recurdyn软件中定义旋耕刀片、刀盘、刀轴之间的连接关系，设置部件运动参数，并导出刀轴几何模型；最后，将刀轴模型导入EDEM软件，设置相应的材料属性。

1.2.4模拟控制参数 整个模拟过程中，模拟进程由Recurdyn控制，EDEM计算土壤颗粒运动，Recurdyn计算旋耕刀的运动。本文设置的EDEM模拟时间步长为1e-05 s，约为Rayleigh时间步长的13%，网格尺寸为3倍的最小颗粒半径；Recurdyn计算时间步数为2 000步，模拟总时间2 s，其他参数为默认值。

2 结果与分析

2.1 不同土层扭矩分析

考虑到模拟分析旋耕刀耕作土壤的时间远没有土槽试验时间长，因此，为便于与模拟结果对比，这里仅分析刀轴旋转约一周的试验数据，即取0.6 s耕作时长的试验数据进行分析。对试验数据进行移动平均滤波处理，滤波窗口宽度为5，结果如图4所示。可见，不同耕作深度的扭矩值相差较大；刀轴的负荷变化规律基本一致但并不完全相同，这可能是由于土壤不同深度耕作阻力不同所引起。

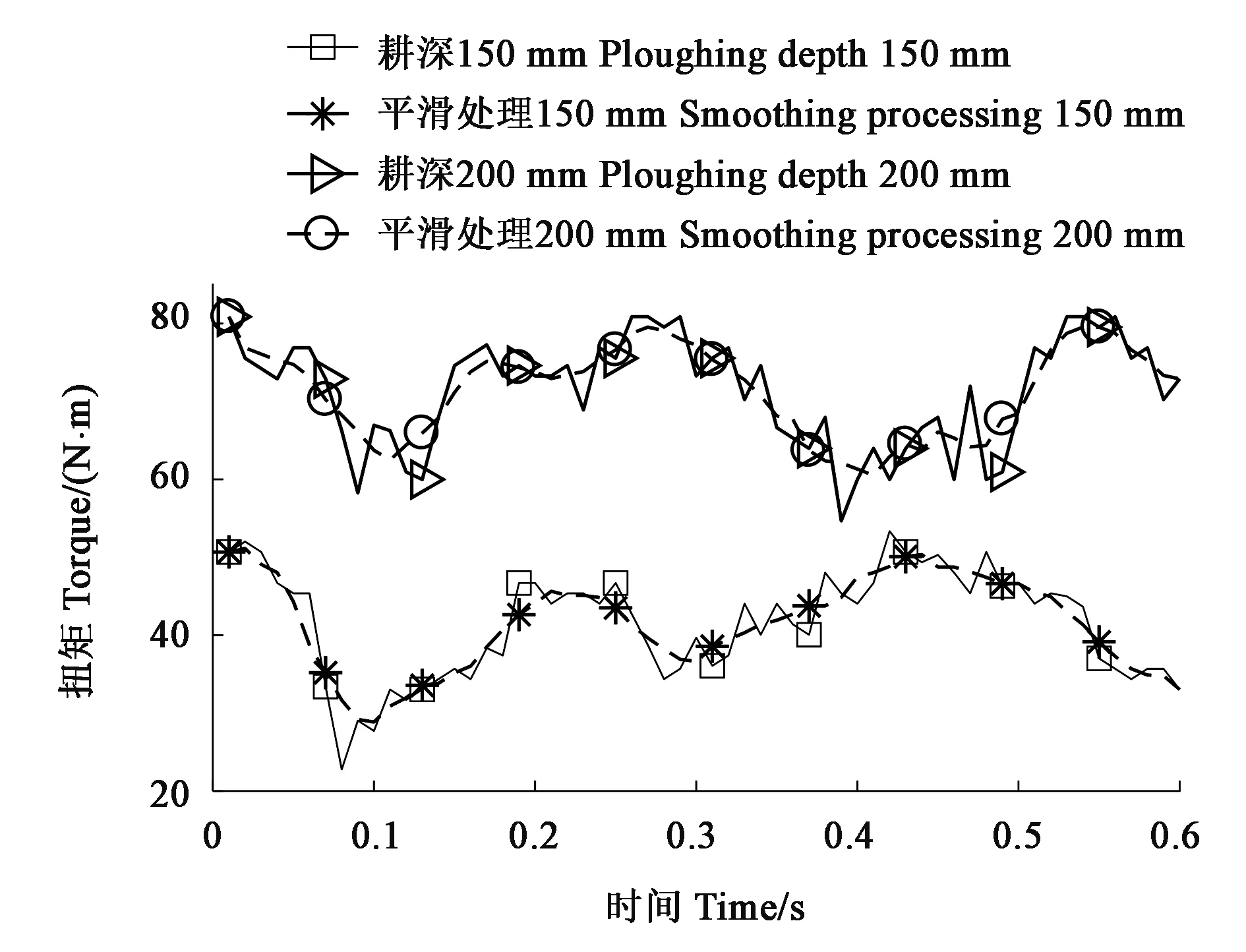
图4 土槽扭矩分析Fig.4 Torque analysis of soil tank

2.2 耕作模型构建与分析

所建立的左侧刀辊完整耕作模型如图5所示，耦合模拟过程如图6所示。可以看出：模拟过程中，土壤颗粒随着旋耕刀的运动抛向空中，与实际耕作现象一致，能够真实反映耕作过程。

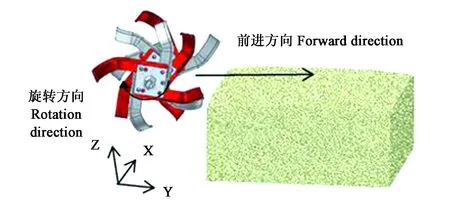
图5 耕作模型Fig.5 Tilling model

图6 耦合模拟过程Fig.6 Co-simulation process

2.3 模拟结果分析

2.3.1单刀盘负荷分析 图7所示为旋耕刀刀盘所受扭矩的变化规律。可见，刀盘1、刀盘3的负荷波动大于刀盘2的波动，这是因为刀盘的布局会影响其切削时所受到的阻力，刀盘2位于中间，刀盘1、刀盘3切削土壤时的扰动会引起刀盘2的切削区域土壤松动，从而导致刀盘2切削时的阻力有所减小。同时，不同刀盘同一时刻的扭矩并不相等，这是因为3个刀盘虽然在同一刀轴上，但同一时刻的切入角并不一致，切入的土壤深度也不一致，从而导致刀盘之间的扭矩不相等。因此，从刀轴的负荷分析，其所受的等效扭矩并不简单地等于单个刀盘受到的扭矩与刀盘数量的乘积。

图7 不同耕深刀盘的模拟扭矩Fig.7 Simulation torque of tool holder at different ploughing depth

2.3.2刀轴扭矩对比分析 从图8可以看出，试验扭矩曲线和模拟扭矩曲线变化规律基本一致，这表明离散元与多体动力学的耦合能够较好地反映刀轴在耕作过程中所受到的扭矩变化规律。误差较大反映出所建立的土壤模型尚不能精确反映试验土壤的性质，耕作深度为150、200 mm时的最大相对误差分别为14.01%、11.49%，表明土壤模型精度还有待提高。但是，模拟扭矩曲线的变化规律较为明显，这可能是因为深处的土壤状态相对更为稳定，从而导致耕作过程中刀轴受到的等效扭矩变化随耕作部件切入深度变化较为明显。从最大值和最小值出现的时间位置可以看出，二者并不完全一致，这是因为土槽试验过程中试验车的行进速度难以精确保证，有一定的波动，导致了与模拟结果的差异。

图8 试验与模拟刀轴扭矩对比Fig.8 Comparison between simulation and experimental torque of cutter shaft

3 讨论

本文以重庆地区典型的微耕机用旋耕刀辊和土壤为对象，开展了刀辊耕作过程的土槽试验。传统的农业机械及其关键部件试验多在田间进行，受到季节、气候等因素的制约，试验条件(如环境温度 、土壤湿度 、密实度等)不一致，难以确保农机具作业保持相同的土壤环境，为此，本文选择在室内土槽试验台上进行试验。

建立精确的土壤模型是耕作模拟的基础，也是模拟中的一大难点。鉴于土壤力学特性的复杂性，采用有限元方法难以满足研究需要，因此，诸多研究者尝试应用离散元法中不同的颗粒接触模型[27,30-32]建立土壤模型。不同的模型适用于不同的土壤类型，实际应用中，应依据土壤是否可以压缩、是否粘结等作为模型的选择依据[33]。基于离散元和多体动力学理论，采用非线性粘弹性塑性接触模型，借助EDEM2018和RecurdynV9R1软件平台实现了刀轴耕作过程的耦合模拟分析。耕深为150、200 mm两种工况下的模拟结果表明，同一刀轴上不同刀盘受到的扭矩值不一致，以3刀盘为例，中间位置的刀盘扭矩值较为稳定，波动较小，究其原因可能是两侧相邻刀盘的耕刀耕作影响了该位置耕刀的耕作区域。而且，同一刀轴上不同刀盘的扭矩变化规律相似，但数值并不一致，因此，整个刀轴所受的等效扭矩不能简单地理解为单个刀盘受到的扭矩与刀盘数的乘积。只有研究整个刀轴的耕作过程，才能准确地分析各因素对刀轴负荷的影响，为微耕机作业性能的优化提供参考。

试验与模拟的对比分析结果表明，两种耕深工况下刀轴等效扭矩的变化规律基本一致，模拟值与试验值的最大相对误差分别为14.01%和11.49%。而且，就等效扭矩变化曲线而言，耕深大的较耕深小的变化规律更为明显，究其原因可能是深处的土壤状态更趋于稳定。就耕作扭矩而言，其变化规律类似于正弦函数，这与Matin等[16]对单刀盘的研究结论是一致的。理论上分析，整个刀辊的扭矩可以看作是由其所包含的任一刀盘在其自身初相位及其余刀盘初相位情况下的扭矩之和，但是，实际耕作中，由于刀具扰动土壤的作用，导致二者之间存在一定的差异。因此，后续可在研究单刀耕作对土壤扰动[34]的基础上进一步深入研究多刀耕作对土壤的扰动作用。

土壤颗粒接触模型及参数对模拟过程和结果有重要影响。本研究采用的EEPA颗粒接触模型能够客观反映粘性土壤耕作过程，但是，分析结果表明，典型耕作深度下刀轴所受扭矩的试验值与模拟值最大相对误差较大，这极有可能是土壤模型与试验土壤间的物理性质差异所致，误差来源可能是接触模型或接触参数，因此，后续需进一步研究土壤模型的建立方法，以提高模型精度。