几何辅助线的根源探索

李想

【摘要】几何在数学中不同于代数，浑然天成的题目，简洁的条件和结论却蕴含着不简单的思想.几何辅助线作为连接条件与结论的桥梁，是几何中的难点，本文就几种简单几何辅助线的根源进行探究，寻求几何辅助线的规律性

【关键词】平面几何;辅助线

平面几何曾被许多科学家、数学家称为“思维的艺术体操”.在全国各省市的中考中，几何证明题也是这场选拔性考试的分水岭，题目主要考查考生对基本图形的识别能力以及逻辑推理的能力，正确地连接辅助线是解决平面几何问题的关键.但是，对许多学生来说，辅助线的选取只能就提论题，几何问题的思维方法很难形成规律性，这也是长期以来，教师觉得几何难教，学生觉得几何难学的原因.笔者在近日的教学中，以一道一题多解的几何题为例，和学生分享辅助线的规律性，学生收获颇丰.

例 如圖1所示，等腰直角△ABC中，AB=AC，P是BC中点，PD⊥PE，求证：PD=PE.

本题是一道等腰直角三角形的基础题，题目本身并不难.

方法一 连接AP，如图2所示，易证△BPD≌△APE，从而证得PD=PE.但学生思考的是辅助线连接AP有什么规律可循吗？

了解简单基础的平面几何基本图形，是研究平面几何的基础，实际上这也正是辅助线的由来，因此，对于辅助线连接AP，先和学生分享了一个简单的数学模型：

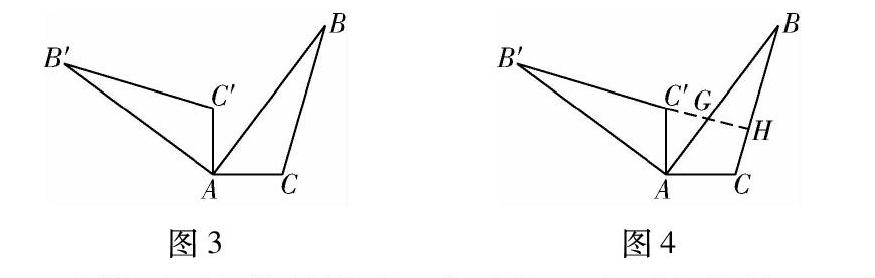
如图3所示，将△ABC绕点A逆时针旋转90°，得到△AB′C′，易证B′C′⊥BC.（简释：如图4所示，延长B′C′交AB于点G，交BC于点H，∠B=∠B′，∠BAB′=∠B′HB=90°）

上述模型可以简单说成三角形绕一个顶点旋转90°后，旋转前后该顶点所对的边垂直.那么当PD⊥PE时，如何证明PD=PE呢？旋转可以给我们提供一种思路，思考有没有PD所在的三角形，旋转90°之后可以得到PE所在的三角形呢？于是就有了连接AP，当然题目中天然的垂直和相等让题目更加和谐，即第三边BD⊥AE，AP=BP.旋转的思路在证明互相垂直的线段相等时有着广泛的应用.

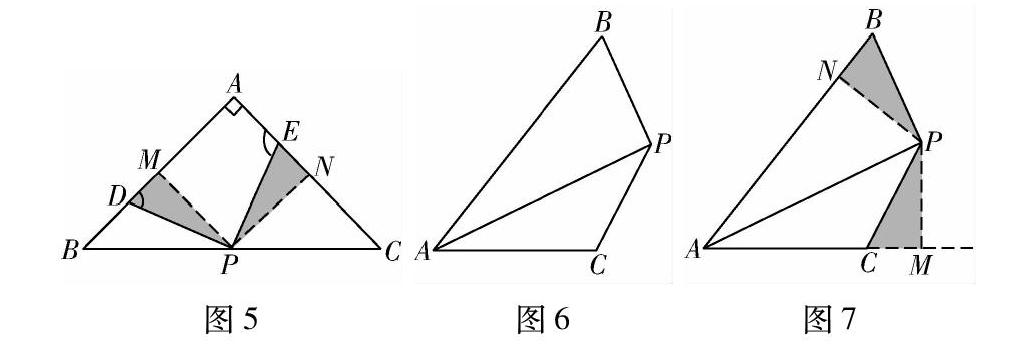
方法二 如图5所示，过点P作PM⊥AB，PN⊥AC，易证PM=PN（连接AP用角平分线的性质，或PM=BPsinB，PN=CPsinC），接下来证明△PMD≌△PNE，从而证得PD=PE.

过点P分别向AB，AC两边作垂线是怎样想出来的呢？再看一个基础模型，如图6所示，在四边形ACPB中，AP平分∠BAC，∠B+∠C=180°，易证PB=PC（简释：过点P作PN⊥AB，PM⊥AC，PM=PN，又∠B=∠PCM，△PCM≌△PBN，如图7所示）.该模型常被称为对角互补模型，作垂线的思路来源于角平分线的性质，并且一箭双雕，不仅边相等，还得到了两个直角.例题中，四边形ADPE是对角互补的四边形，而AP恰好是角BAC的角平分线，于是考虑作双垂线.但不同的题目要学会灵活运用.

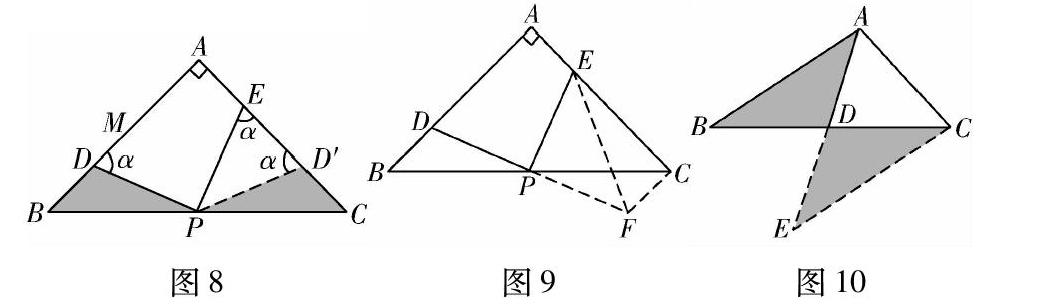
方法三 四边形ADPE对角互补，易证∠ADP=∠PEC，考虑等腰直角三角形的对称性，取点D关于AP的对称点D′，则PD=PD′，用对称法将PD′作为桥梁，再通过证明△PD′E是等腰三角形即可完成证明，对称法也是对角互补模型常见的思路.

方法四 如图9所示，延长DP至F使得DP=PF，连接FC，EF，易证△DPB≌△FPC，CF∥AB，∠FCA=90°，E，C，F，P四点共圆，∠EFP=∠ACB=45°，即△EPF是等腰直角三角形，所以PE=PF=PD.

方法四常被称为倍长中线，如图10所示，通常题目中已知中点时，考虑用倍长中线法构造三角形全等，从而通过边之间的等量关系和位置关系为已知和求证有效地搭建桥梁，完成间接证明.

结束语

几何的和谐之美在于浑然天成，几何方法瀚如星海，有繁简，但无好坏之分，每种方法的背后必有根源，无论教几何，还是学几何，深度探究几何辅助线的根源都是学习几何的法宝.

【参考文献】

[1]郭光福.平面几何辅助线的应用[J].中学数学教学参考，2016（18）：41-42.