数控机床可靠性评估及预防维修的对数线性虚龄过程方法
2020-03-13
(江苏海洋大学应用技术学院,江苏 连云港 222069)
数控机床的质量指标主要有性能、可靠性和维修性,性能代表机床使用价值的主要指标;可靠性代表机床在规定的时间内和规定的条件下完成规定功能的能力。当前,机床正朝着精密化、柔性化、集成化、自动化和智能化方面迅速发展,随着复合功能和密集型技术的引入,机床在使用过程中发生故障概率的增加,其性能也随之降低,因此提高数控机床的可靠性势在必行[1-2]。
1 数控机床可靠性评估及预防维修存在的主要问题和研究内容
目前,数控机床的可靠性与维修性分析方面已取得一定的成绩,高档数控机床与基础制造装备等16个国家科技重大专项已列入《国家中长期科学和技术发展规划纲要(2006-2020)》,其是我国到2020年科技发展的重中之重。其中,数控机床可靠性研究已被列入重大专项的基础共性技术之一。
1.1 存在的主要问题
(1)数控机床的故障数据受维修的影响,一般非独立性分布,且其发生故障后的维修类型通常为不完全维修,但目前的评估模型过多地依赖于不可修系统的统计分布模型。
(2)幂律过程(Power Law Process,PLP)模型和对数线性过程(Lead Logistics Provider,LLP)模型同是非齐次泊松过程(Non-homogeneous Poisson Process,NHPP)的模型之一,该过程模型适合于具有故障趋势可修系统的故障分析,但在数控机床的故障趋势分析中,多使用幂律模型,而缺少对对数线性过程模型的研究。
(3)目前对数控机床可靠性指标的评估,多是点式估计,缺少对可靠性指标的区间估计。
(4)缺少对数控机床非等周期任意维修质量的不完全预防维修的研究。
1.2 主要研究内容
(1)通过对故障数据的综合趋势检验确定故障的维修类型,选取相应的数控机床可靠性评估模型与方法。
(2)研究幂律过程模型和对数线性过程模型在数控机床可靠性分析及预防维修中的适用条件。
(3)分析对数线性过程模型在数控机床可靠性分析中的应用,给出机床的累积平均无故障工作时间、累积故障数、给定时间的可靠度、一定可靠度下的工作时间等可靠性指标的点估计和区间估计。
2 数控机床预防维修的对数线性虚龄过程方法
可修系统的可靠性分析不同于不可修系统的可靠性分析,这是因为维修可修部分或全部恢复可修系统的可靠性,使之恢复如下几种状态:① 修复如新;②修复如旧;③好于旧但次于新;④好于新;⑤次于旧。其中后两种维修状态不常见,一般只分析前三种维修状态,即最小维修、最大维修及不完全维修[3-4]。在数控机床的可靠性分析中,若维修使其修复如新,则可用Weibull等分布分析其故障间隔时间(time between failure),用对数正态等分布分析其维修时间,此时机床的故障不具有某种故障趋势。若机床的累积故障数随使用时间表现出某种增大或减小的趋势,可用非齐次泊松过程的最小维修理论分析其可靠性。事实上,工程实践中的大多数维修属于不完全维修,最小维修和最大维修只是不完全维修的两种极端状态。目前,在采集数控机床的现场故障数据方面,多采用一个预防维修或大修周期内的数据,且在预防维修或大修期间,只对发生故障的部位进行最小维修,对于其他部位不予维修。另一方面,数控机床的初始观察时间和初次使用时间一般不同,其故障率不为零,在这种情况下用初始故障率为零的PLP模型分析其可靠性不合理。此时,可用对数线性过程模型描述其故障过程。
3 数控机床预防维修的对数线性虚龄过程技术
3.1 实验方法
选取同型数控机床若干台,且其现场使用环境及维修水平相似,现场故障数据为右截尾时间[5]。
3.2 故障数据及维修时间的综合趋势检验
用图形方法和统计分析方法对搜集整理的故障数据及维修时间进行综合趋势检验。其中,图形方法包括Nelson-Aalen 图检验和总时间检验(total time on test,TTT)。
用图形方法初步获得故障数据的故障趋势后,可进一步用统计分析方法对该数据进行综合趋势检验。首先用刘易斯鲁滨孙(lewis-Robinson,LR)检验和正态性(Jarque,J)检验判断故障数据是否为普通更新过程(ordinary refresh process,ORP)数据,若是则表明故障数据独立同分布,可用Weibull等经典统计分布分析该数据;若故障数据不满足普通更新过程,可用拉普拉斯(Laplace)检验和梅特罗波利斯-黑斯廷斯算法(Metropolis-Hastings algorithm,MH)检验判断其是否满足非齐次泊松过程。
3.3 幂律模型和对数线性模型选择
幂律过程模型是非齐次泊松过程模型的一种,其强度函数为:
u(t)=λβtβ-1(λ>0,β>0,t≥0)
(1)
式中:λ为尺度参数;β为形状参数。
当β=1时,故障强度为常数,产品处于偶然失效期;当β< 1时,故障强度减小,产品处于早期失效期;当β>1时,故障强度增大,产品处于耗损失效期。
非齐次泊松过程的另一种模型为对数线性过程模型,其强度函数为:
u(t)=exp(a+bt),-∞ (2) 式中:a、b为模型参数。 当a=0时模型退化为齐次泊松过程模型;b<0时,产品相邻故障间隔有变大的趋势;b>0时,产品相邻故障间隔有变小的趋势。 假定共有k台机床,其中第j台机床在统计时间区间[t0j,Tj]发生了nj个故障,第i个故障发生时间是ti,j(i=1,2,…,nj;j=1,2,…,k)。设t0,j、t1,j、t2,j、…、tnj,j、Tj为故障时间,Tj代表截尾时间。设故障时间ti-1,j至故障时间ti,j之间的故障间隔时间为xi,j,即xi,j=ti,j-ti-1,j,则故障间隔时间分别为x1,j、x2,j、…xnj,j、Tj-tnj,j。首先,基于式(1)和式(2),可用极大似然法分别给出幂律过程模型和对数线性过程模型所描述故障间隔时间的对数似然函数。赤池信息准则(Akaike Information Criterion,AIC)、贝叶斯信息准则(Bayesian Information Criterion,BIC)基于极大似然估计法,并利用了似然估计性质。因此,可用 AIC、BIC 值选择最佳模型。 基于对数线性过程理论,应用极大似然估计法可得各参数的极大似然估计值,然后将其代入各可靠性指标公式即可得相应的点估计。模型参数和可靠性指标的区间估计可由Fisher信息矩阵法求得。其中,参数的方差矩阵为: (3) 式中:Δ11、Δ12、Δ21、Δ22分别为模型参数极大似然估计的二阶偏导数和导数。 (4) 据此,可给出其区间估计: (5) 当数控机床磨损加剧进入损耗期时,可考虑对其进行预防维修。结合故障率增加因子和维修对其实际役龄的影响,则数控机床第i次预防维修后的故障率为: hi(x)=θi-1exp(a+b)(x+qti-1)),0≤x≤Ti (6) 式中:q为恢复因子;ti为第i次预防维修时间;θ为预防维修后的故障率增加因子,θ>1;Ti为第(i-1)次至第i次预防维修区间。 在实际维修中,每次预防维修程度因不同的故障模式和部位而有所差异,所以Kijima把维修恢复因子定义为[0,1]区间的随机变量。Wu也指出,故障率增加因子θ应在某一区间而非某一固定值。所以,可假设维修恢复因子q(0 ≤q≤ 1)和故障率增加因子θ(u≥θ≥ 1)服从均匀分布,规定当数控机床的可靠度随时间的变化降低到要求的Rmin时,对系统进行一次不完全预防维修,即每一个预防维修区间的最小可靠度为Rmin,在得出预防维修周期Ti(i=1,2,…,N)后,以数控机床长期平均维修费用率C(N)最低和可用度A最大为目标函数,求取最佳维修次数N。 预防维修的对数线性虚龄过程技术路线如图1所示。 图1 预防维修的对数线性虚龄过程技术路线 (1)对故障数据及维修数据进行综合趋势检验,避免过多地依赖统计分布模型。 (2)对于数控机床等复杂的可修系统,当故障数据具有明显的故障趋势时,在可靠性分析中,应选用“过程”模型而非“分布”模型。 (3)当数控机床的初始故障强度不为零时,应优先选用对数线性过程模型,而非幂律过程模型。 (4)最小维修和最大维修是不完全维修的两种极端状态,在可靠性分析中,应使用综合趋势检验方法,防止从一个极端走入另一个极端。 (5)本项目所提虚龄混合模型中的最小维修费用及预防维修费用均为平均值,当数控机床处于损耗阶段时,预防维修费用一般随时间的增大而增大,亦可认为该费用为时间的一次函数。 (1)对数线性过程模型比幂律过程模型在数控机床的初始故障强度不为零时更接近工程实际情况。 (2)对数线性虚龄过程方法不仅可给出数控机床可靠性指标的点估计,而且可给出其区间估计。可解决数控机床可靠性分析中对可靠性指标点估计的研究较多,但对其区间估计研究不足的问题。 (3)对数线性虚龄过程混合模型,在所需可靠度下,可给出任意维修质量的非等周期预防维修时间和最佳维修次数,使该模型更接近数控机床可靠性分析的实际情况。3.4 模型参数和可靠性指标的点估计及区间估计
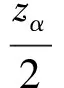
3.5 数控机床任意维修质量的虚龄混合模型建模及非等周期预防维修

4 数控机床预防维修的对数线性虚龄过程关键技术
5 小结
