液压混合动力车辆联合制动系统控制
2020-03-1322
22
(1.北京信息科技大学机电工程学院, 北京 100192;2.北京电动车辆协同创新中心, 北京 100192)
引言
随着能源与环境问题的日益严峻,混合动力车辆因为燃油经济性和排放性较好,所以成为当前汽车节能减排领域研究的重点。而液压混合动力车辆在工作中可以实现短时间内的能量快速充放,同时通过再生蓄能器对制动能量进行回收,并将回收的能量再次应用于再生制动或再生驱动。但液压混合动力车辆的制动系统构造复杂且各系统之间的协调匹配不甚合理,若控制策略选择不当,将很难对制动系统进行最优控制,从而使能量回收率亦难以得到提升。
目前模糊控制已经广泛应用于车辆控制系统,且存在诸多针对模糊控制策略的优化方法,曹万仓等[1]基于模糊控制原理设计了液压混合动力车辆制动能量模糊控制策略,在确保制动安全性的前提下大幅提高了能量回收率。刘洋等[2]通过将模糊控制理论运用于液压混合动力装载机的驱动与联合制动系统,有效降低了整车燃油消耗率。于忠杰等[3]使用粒子群算法对液压混合动力装载机的模糊控制器的控制规则进行了最优化设计,使整车制动能量回收率得到明显提高。林慕义等[4]采用遗传算法对装载机联合制动系统中影响能量回收率的主要参数进行了优化,使优化后的整车能量回收率得到显著提高。而本研究采用的自适应神经模糊系统是一种将神经网络与T-S模糊推理相结合的系统,因此兼具二者优点,即模糊推理的建立过程不依赖对象模型且具有很强的自学习、自识别及自适应能力[5-6]。
本研究针对液压混合动力车辆制动系统结构复杂且不易控制的特点,首先搭建液压混合动力装载机联合制动系统的Simulink仿真模型,并利用自适应神经模糊控制策略对传统模糊控制器进行优化,将优化后得到的ANFIS控制器载入到仿真模型中进行优化前后的对比分析,最后利用dSPACE进行联合制动系统试验验证,以期实现控制效果的有效性。
1 联合制动系统结构与原理
本研究的液压混合动力装载机的联合制动系统包括再生制动系统、电液制动系统以及动力调节系统。再生制动系统和电液制动系统通过二次元件和扭矩耦合器并联在一起共同对车辆进行制动。再生制动系统通过二次元件将车辆制动过程中的动能和惯性进行回收,并将其转化为液压能储存到再生蓄能器。此外,再生蓄能器又可以为电液蓄能器进行充液,作为电液制动系统的动力源来辅助完成电液制动过程[7]。联合制动系统整体原理图如图1所示。

图1 联合制动系统整体原理图
2 联合制动系统建模
再生制动系统包括再生制动蓄能器以及变量泵/马达等,电液制动系统由比例减压阀等组成,而动力调节系统由3个电磁换向阀等组成,利用相关公式分别建立上述3个子系统中各模块的数学模型如下:
2.1 再生制动系统
再生蓄能器充液数学模型:
(1)
式中,Q—— 充液流量
V0—— 蓄能器有效容积
n—— 气体多变过程指数
p0—— 蓄能器充气压力
p—— 蓄能器出口压力
C1—— 蓄能器充液液容
变量泵/马达动态数学模型:
(2)
式中,V′ —— 变量泵/马达的排量
d—— 柱塞直径
Z—— 柱塞数量
D—— 分布圆直径
λ—— 斜盘倾角与变量缸活塞位移增益
y—— 变量缸活塞位移
2.2 电液制动系统
比例减压阀数学模型:
(3)
式中,Q—— 减压阀节流口的流量
Cd—— 流量系数
A1—— 主进油口到工作进油口的节流口开口面积
ρ—— 液压油密度
p1—— 蓄能器出口压力
p2—— 蓄能器入口压力
2.3 动力调节系统
电磁换向阀数学模型:
(4)
式中,Q—— 流经电磁换向阀的流量
Cd—— 流量系数
A1—— 过流面积
ρ—— 液体密度
pV—— 电磁换向阀进口压力
p′V—— 电磁换向阀出口压力[8]
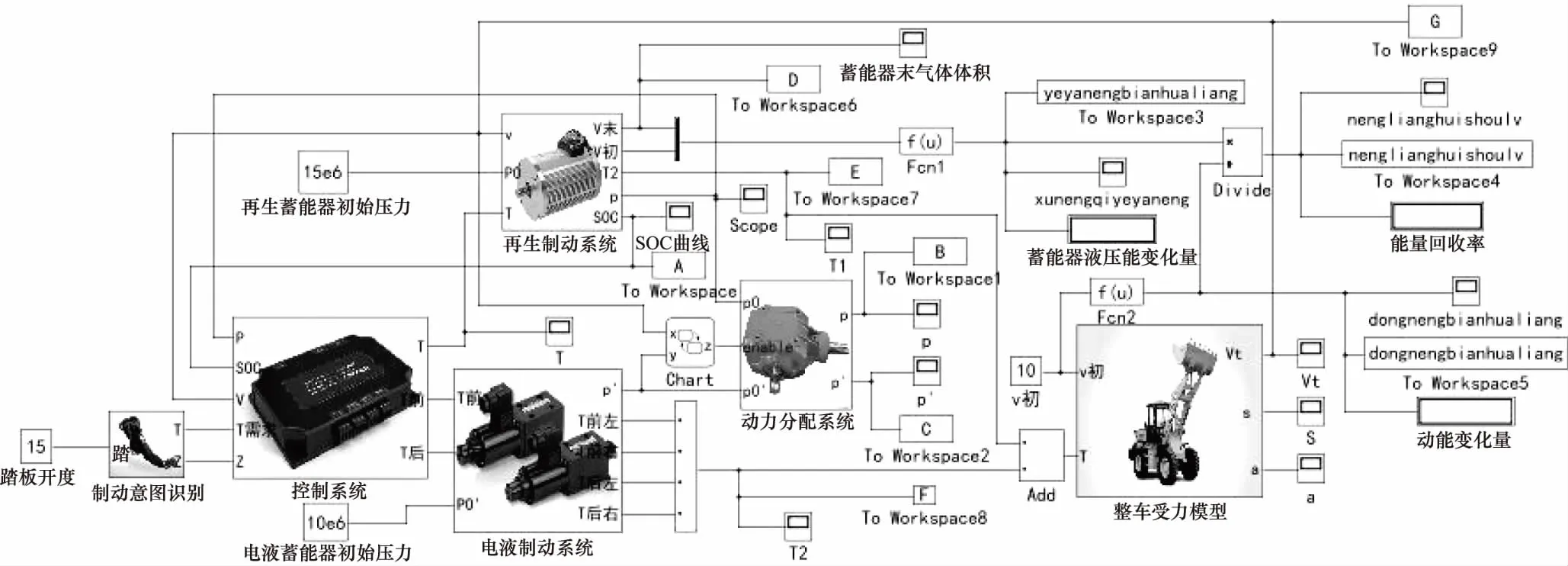
图2 联合制动系统仿真Simulink模型
2.4 搭建Simulink仿真模型
利用上述数学模型式(1)~式(4)并结合其他有关公式在Simulink中搭建联合制动系统仿真模型,如图2所示。
3 自适应神经模糊控制系统设计
3.1 自适应神经模糊控制系统
ANFIS根据样本数据,通过自适应建模法来建立模糊推理系统,并通过神经网络用误差反向传播算法或混合算法来推算出模糊控制系统的模糊控制规则和隶属度函数,而非依赖专家经验来进行主观归纳与总结,因此有效解决了那些特性不为人们所完全了解或特性非常复杂的系统问题,实现了更好的控制效果[9-10]。
3.2 建立初始ANFIS
本研究从联合制动系统的实验数据中选取部分数据作为样本数据,在样本数据中以SOC(再生蓄能器)、V(车速)和Z(制动力矩)作为输入量,以K(转矩分配系数)作为输出量,然后以此作为训练数据对下文创建的ANFIS控制器进行训练。
为降低神经网络的训练难度并提高训练精度,本研究采用min-max法对训练数据进行归一化,使归一化后的样本数据值均在0~1之间。即通过在MATLAB中运行有关程序来调用MATLAB中的自带函数来对样本数据进行归一化,完成归一化后的样本数据将自动保存至MATLAB的工作区以备后续ANFIS工具箱的调用。
在MATLAB中调出anfisedit工具箱,进入FIS编辑器并新建一个Sugeno型模糊推理系统,依据上述输入量和输出量创建一个三输入单输出的系统。同时And Method设置为prod,Or Method设置为probor,Defuzzification设置为wtaver[11]。通过anfisedit工具箱中的训练数据加载功能将经过归一化处理后的训练数据加载进工具箱,如图3所示。

图3 加载样本数据后的ANFIS编辑器界面
FIS的生成方式设置为Sub.clustering法,且具体参数设置保持原始缺省值。建立完成后的ANFIS控制系统内部结构如图4所示。
由图4可知本系统结构采用多层前向神经网络,各层所属任务及向下一层传递的信息均不同:
第一层为输入层,3个输入点分别代表上述3个输入量。
第二层为模糊化层,覆盖每个输入量的均是6个模糊子集。
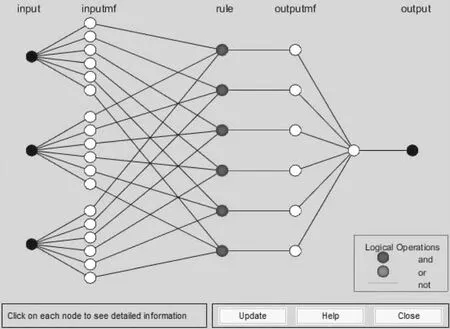
图4 Sugeno型ANFIS系统结构
第三层为模糊规则层,各输入量的模糊子集互相交叉生成6条模糊规则。
第四层为模糊推理层,依据生成的6条模糊规则生成6个输出量的输出函数。
第五层为清晰化层,从ANFIS控制系统输出清晰化后的输出量。
ANFIS编辑器根据训练数据自动选择输入量的隶属度函数类型为高斯型,输出量为线性函数。初始FIS状态下的各输入量对应的隶属度函数曲线,如图5所示。
在图5中,将anfisedit工具箱中的各输入量的6个模糊子集分别进行重新命名。此时各输入量的论域均为[0,1],同时由图5可见,由于以实测数据为基础,故各输入量的隶属度函数划分具有较高的不均匀性。
anfisedit工具箱通过神经网络对输入的训练数据进行推算,得出6条一一对应的模糊规则为:
① IF(SOC ise1)and(Visf1)and(Zisr1)then(Kisu1)
② IF(SOC ise2)and(Visf2)and(Zisr2)then(Kisu2)
③ IF(SOC ise3)and(Visf3)and(Zisr3)then(Kisu3)
④ IF(SOC ise4)and(Visf4)and(Zisr4)then(Kisu4)
⑤ IF(SOC isev5)and(Visf5)and(Zisr5)then(Kisu5)
⑥IF(SOCise6)and(Visf6)and(Zisr6)then(Kisu6)
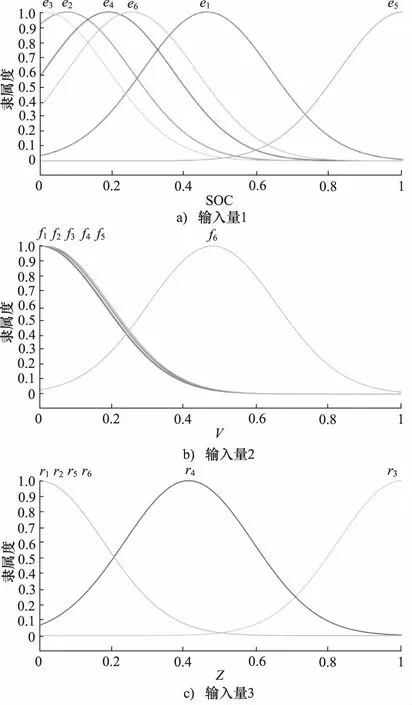
图5 训练前ANFIS控制器隶属度函数划分
3.3 初始ANFIS的训练
在训练初始ANFIS之前需要对各控制参数进行相应的设置:训练算法为BP反向传播算法和最小二乘法相结合的混合算法,而训练次数为20次,训练误差阈值为0。完成初始ANFIS的各项控制参数设置后开始初始ANFIS的训练,最终得到的误差-训练次数关系动态曲线如图6所示,其中横坐标为训练次数,纵坐标为误差。
由图6可见,ANFIS的训练误差在训练次数接近20次时不再发生变化,并最终停留在0.017567,因此,训练次数设定为20次较为合理。
3.4 生成训练后的ANFIS
训练结束后进入anfisedit工具箱的隶属度函数编辑页面,如图7所示, ANFIS经过对训练数据的自学习后,依据训练数据中的最优输出值,各输入量的隶属度函数的模糊子集形状发生明显变化,即隶属度函数被重新划分。此时的ANFIS具有了自适应性,且目标性更强,更易于实现最优的控制效果。将训练后生成的ANFIS控制器保存至MATLAB工作区,以便后续仿真模型的调用。

图6 训练误差变化曲线
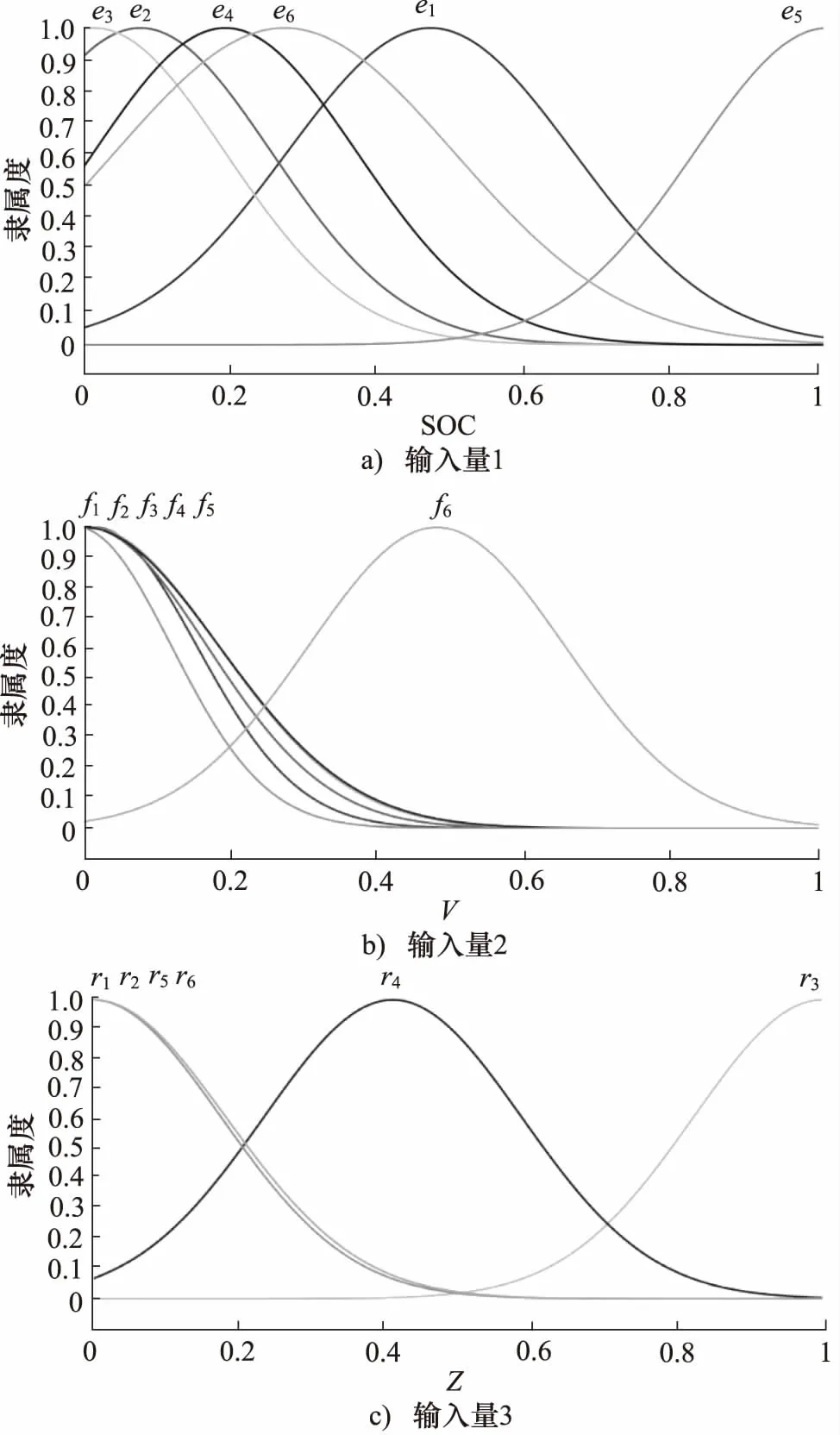
图7 训练后ANFIS控制器隶属度函数划分
4 仿真分析
从MATLAB工作区调用经过训练的ANFIS控制器,并将其载入到联合制动系统仿真模型中,同时选择以下6种工况进行仿真分析。
工况一:初始制动车速10 km/h,制动踏板下探幅度15%,初始再生蓄能器压力15 MPa,初始电液蓄能器压力10 MPa。
工况二:初始制动车速20 km/h,制动踏板下探幅度15%,初始再生蓄能器压力15 MPa,初始电液蓄能器压力10 MPa。
工况三:初始制动车速30 km/h,制动踏板下探幅度15%,初始再生蓄能器压力15 MPa,初始电液蓄能器压力10 MPa。
工况四:制动踏板下探幅度15%,初始制动车速20 km/h,初始再生蓄能器压力15 MPa,初始电液蓄能器压力10 MPa。
工况五:制动踏板下探幅度50%,初始制动车速20 km/h,初始再生蓄能器压力15 MPa,初始电液蓄能器压力10 MPa。
工况六:制动踏板下探幅度100%,初始制动车速20 km/h,初始再生蓄能器压力15 MPa,初始电液蓄能器压力10 MPa。
(1) 不同初始制动车速时,即在工况一、二、三情况下,采集各工况下的再生蓄能器压力曲线,仿真结果对比如图8所示。
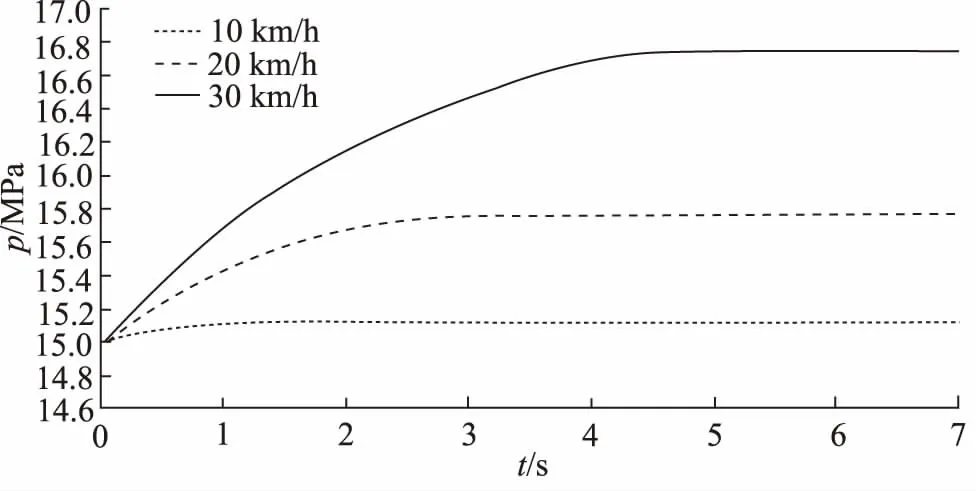
图8 不同初始制动车速时的仿真结果
(2) 不同制动踏板下探幅度时,即在工况四、五、六情况下,采集各工况下的再生蓄能器压力曲线,仿真结果对比如图9所示。

图9 不同制动踏板下探幅度时的仿真结果
由图8、图9可见,在ANFIS控制器的控制下,初始制动车速越快,再生蓄能器压力越高,且均在5 s之前达到稳定值。踏板下探幅度越大, 再生蓄能器压力越低,且均在3 s之前达到稳定值。仿真结果表明,基于自适应神经模糊控制的联合制动系统的反应速度迅速,控制性能较高。
为将仿真结果进行量化,引入以下评价指标[12]。
车辆动能:
(5)
式中,m—— 汽车质量,kg
v—— 汽车末速度,km/h
v0—— 汽车初速度,km/h
液压蓄能器能量:
(6)
式中,V1—— 蓄能器初始体积,m3
V2—— 蓄能器末体积,m3
p1—— 蓄能器压力,MPa
β—— 气体多变过程指数,为无量纲,此处取1.4
能量回收率:
(7)
根据式(5)~式(7),将普通模糊控制以及ANFIS控制2种控制策略下的各对应评价指标进行对比,结果如表1所示。
由表1可见,基于ANFIS控制下的联合制动系统,在6种不同工况下回收的液压能以及能量回收率均高于普通模糊控制下的相应结果,且初始制动速度越高,回收的液压能和能量回收率就越高,而制动踏板开度越大,回收的液压能和能量回收率也就越高。此外,对比结果也表明车辆动能的变化量只与车辆初始制动车速有关,而与控制策略无关。

表1 不同控制策略下的仿真结果对比
5 硬件在环试验
5.1 试验基本原理
如图10所示,搭建联合制动系统试验台架,并将台架各实物部件与dSPACE的扩展板连接,然后通过在模型中添加相应转换接口模块来将扩展板与仿真模型进行连接,最终实现仿真模型与实验设备的结合。最后将修改后的模型编译进dSPACE的控制软件Controldesk,然后启动试验设备进行硬件在环试验。

图10 联合制动系统试验台架
5.2 试验结果分析
(1) 对不同初始制动车速时的工况一、工况二、工况三条件下的联合制动系统进行硬件在环试验,并采集各工况下的再生蓄能器压力曲线,所得仿真与试验结果对比如图11所示。
(2) 对不同制动踏板下探幅度下的工况四、工况五、工况六条件下的联合制动系统进行硬件在环试验,并采集各工况下的再生蓄能器压力曲线,所得仿真与试验结果对比如图12所示。

图11 不同初始制动车速时的试验与仿真结果对比
由图11和图12可见,初始制动车速越大,制动踏板下探幅度越小,试验曲线与仿真曲线越接近,而初始制动车速越小,制动踏板下探幅度越大,试验曲线波动越明显,这是由低车速紧急制动造成的,但此时的波动亦在可接受范围内,仿真曲线与试验曲线基本一致。因此试验结果证明了仿真结果的可靠性,以及基于自适应神经模糊控制策略的正确性。
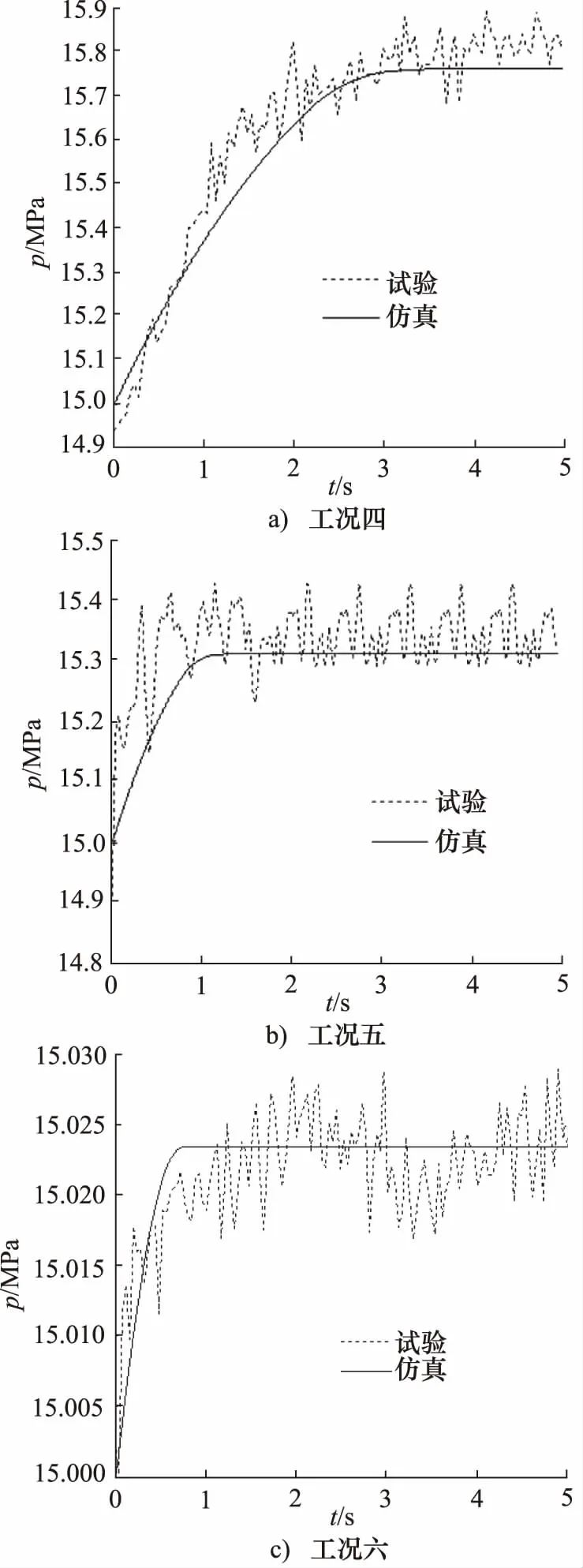
图12 不同制动踏板下探幅度时的试验与仿真结果对比
6 结论
(1) 与普通模糊控制策略相比,ANFIS控制器在制定隶属度函数以及模糊规则时的自适应性和目标性更强,更易于实现最优的控制效果;
(2) 硬件在环试验与仿真的结果表明,采用ANFIS控制器的装载机联合制动系统的能量回收率得到提升;
(3) 基于ANFIS的联合制动系统控制器有效提高了整车的控制性能和经济性能,为相关控制器的优化设计提供了依据。
