液驱多维力加载系统的CMAC-PID复合控制
2020-03-13赵劲松王春发徐嘉祥马志雷赵子宁
赵劲松 王春发 杨 涛 徐嘉祥 马志雷 赵子宁
(1.燕山大学河北省重型机械流体动力传输与控制实验室, 河北秦皇岛 066004;2.浙江大学流体动力与机电系统国家重点实验室, 浙江杭州 310027;3.燕山大学机械工程系, 河北秦皇岛 066004)
引言
目前在工程中对某构件进行力学性能检测时,主要采用单轴拉压力检测,然而复杂的构件在实际工程中需要承受复杂应力环境,采用传统单轴拉压力检测容易使构件检测数据不充分[1]。以并联机构为主体的多维力加载系统可以有效复现构件所处的复杂应力环境,相比于串联机构具有承载能力强、无累计误差等优点[2]。与此同时,多维力加载系统也存在一些不足,如各通道输出力存在交联耦合力,控制精度有待提高等问题[3-5]。
PID控制器是工业控制中使用最普遍的控制器,具有原理简单、使用方便和鲁棒性较好等特点,然而PID控制器在机理复杂、时变和强非线性的控制系统中随动性较差[6-7]。为弥补PID控制器的不足,引入小脑模型神经网络控制器(Cerebellar Model Articulation Controll,CMAC),CMAC早期主要应用在机器人控制中,如机器人行走、视觉跟踪、机器人运动学、动力学控制等领域。HU等[8]把CMAC引入到机器人行走的控制中,用以提高机器人行走的抗干扰性。郭红梅等[9]采用CMAC与PID并行控制的方法,解决四旋翼无人机强耦合问题,提高四旋翼无人机姿态跟踪效果。岳学磊等[10]将CMAC与PID控制器结合构成CMAC-PID复合控制器,用以提高无刷直流电机控制精度,减小超调量。因而分析CMAC与PID控制器结合所构成的复合控制策略,对多维力加载系统控制特性的影响意义重大。
本研究在多维力加载系统三自由度力控工况下,对比CMAC-PID复合控制器与PID控制器的控制性能。通过仿真、实验,验证了CMAC-PID复合控制器在降低通道间耦合力,提高多维力加载系统力控精度的有效性。
1 多维力加载系统建模
1.1 机构动力学建模
本研究以Stewart平台为多维力加载系统的主体结构,由上平台、下平台、伺服作动器以及胡克铰组成,作动器通过胡克铰与上、下平台连接,如图1所示。多维力加载系统输出的广义空间作用力,可分解为沿x,y,z轴的力Fx,Fy,Fz和绕x,y,z轴的力矩Mx,My,Mz。

图1 多维力加载系统示意图
多维力加载系统进行周期力加载试验时,由于上平台位姿呈周期性变化,系统的惯性力不可忽略。因此,该多维力加载系统平移方向力平衡方程可简化为:
(1)
式中,F′ —— 多维力加载系统和被试工件相互作用力
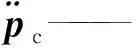
Ln—— 单位向量矩阵
mB—— 上平台质量
g—— 重力加速度向量
多维力加载系统转动方向的力矩平衡方程为:
(2)
式中,M′ —— 多维力加载系统与被试工件间相互作用力矩
IB—— 上平台坐标系下系统转动惯量矩阵
ω—— 世界坐标系下动坐标系角速度
T—— 上平台坐标系与世界坐标系之间旋转变换矩阵
B—— 上平台铰点动坐标矩阵
考虑到伺服作动器活塞杆惯性力,活塞杆与液压缸转动惯量,活塞杆重力,液压缸重力,整个并联机构的动力学方程为:
(3)
式中,Jf,F—— 并联机构力雅可比矩阵
Ms—— 广义质量矩阵
Cs—— 科式向心项矩阵
Gs—— 重力项矩阵
Fo—— 多维力加载系统广义输出力矩阵
由于Ms为非对角阵,各通道输出力存在耦合现象。
1.2 液压动力元件建模
受安装空间限制,多维力加载系统中采用伺服阀控非对称缸的单通道力控系统。与伺服阀控对称缸相比,伺服阀控非对称缸具有系统固有频率不同,正反向运动的开环增益不同等特点[11],在对控制系统进行建模时需要综合考虑此类因素。其物理模型主要由伺服阀、伺服放大器、非对称液压缸、拉压力力传感器、位移传感器、等效负载、控制器等环节组成。
通过构建伺服阀控非对称缸单通道力控系统模型,对系统进行时域特性分析,用以判断多维力加载系统系统的稳定性及动态响应性能。单通道力控系统原理图如图2所示。
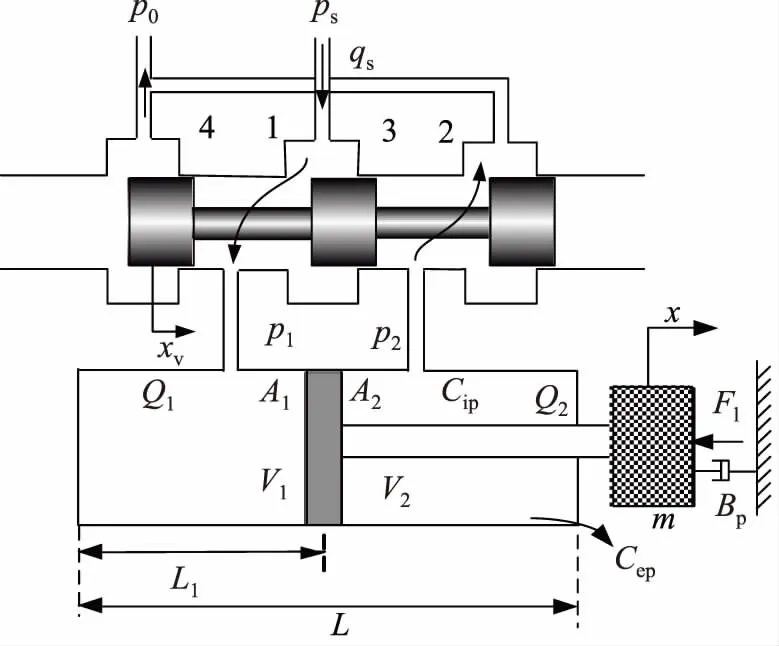
图2 单通道力控系统原理图
定义非对称缸活塞两端受力面积比为:
(4)
式中,A1,A2分别为无杆腔、有杆腔活塞杆面积。
定义负载压力为:
(5)
式中,p1,p2分别为非对称缸无杆腔、有杆腔油液压力;FL为上平台负载等效在各通道外负载力。
定义负载流量为:
(6)
式中,Q1,Q2分别为非对称缸无杆腔、有杆腔流量。
当系统液压固有频率取最小值时,活塞杆处于:
(7)
式中,L,L1分别为活塞杆总长度、无杆腔长度。若在这一点能够满足系统工作需要,使系统达到稳定状态,则系统在其他工作点也能稳定工作,因此选取此点进行建模。
考虑非对称缸正反向运动时开环增益不同,分别列写伺服阀流量方程、液压缸流量连续方程、液压缸力平衡方程,其拉式变换为:
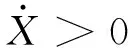
(8)

(9)
式中,Xv—— 伺服阀阀芯位移
Kq1,Kq2—— 分别为活塞杆正向移动、反向移动时的流量增益系数
Kc1,Kc2—— 分别为活塞杆正向移动、反向移动时的流量压力系数
Cop1,Cop2—— 分别为活塞杆正向移动、反向移动时的等效泄漏系数
Ctp—— 活塞杆正、反向移动时的综合泄漏系数
Bp—— 非对称缸黏性阻尼系数
m—— 活塞杆等效质量
k—— 力传感器刚度
X—— 非对称缸活塞杆位移
βe—— 非对称缸体积弹性模量
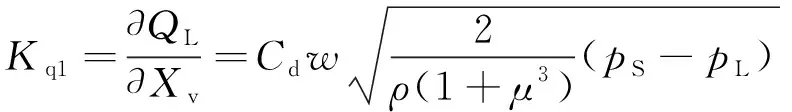
(10)

(11)
(12)

(13)
(14)
(15)
(16)
式中,Cd—— 流量系数
w—— 伺服阀节流口的面积梯度
ρ—— 油液密度
ps—— 供油压力
Cep—— 液压缸外泄系数
Cip—— 液压缸内泄系数
忽略Cop1与Cop2,则阀控非对称缸系统基本方程可为:
(17)
Fl=kX
(18)
此时阀控非对称缸动力机构及负载的控制方框图如图3所示。
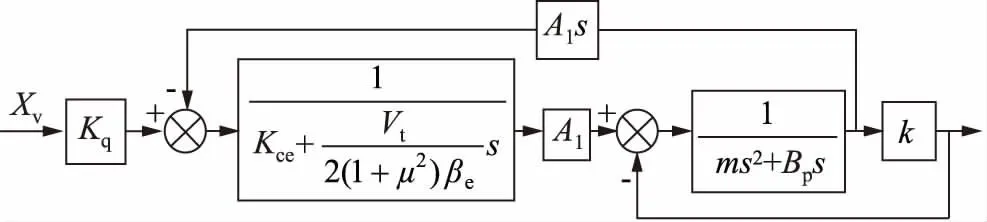
图3 阀控非对称缸动力机构及负载的控制方框图
由图3可以得出,伺服阀阀芯位移与活塞杆输出力之间传递函数为:
(19)
电液伺服阀在建模时可设为二阶振荡环节:
(20)
式中,Kxv—— 伺服阀增益系数
ωsv—— 伺服阀固有频率
ξsv—— 伺服阀阻尼比
由于伺服放大器的频宽,远高于系统液压固有频率,所以可以将伺服放大器等效成为比例环节建模,可表示为:
(21)
式中,Ka为伺服放大器增益系数。综合考虑其他环节建模可得,单通道力控系统传递函数框图如图4所示。
2 CMAC-PID复合控制器设计
2.1 CMAC网络结构
CMAC是J.S.Albus[12]在1975年根据小脑皮层工作特点提出的一种表格查询自适应控制器,这种控制器能够很好的处理不确定性与非线性问题。与其他神经网络算法相比,CMAC响应速度快、结构简单且占用内存小。CMAC网格结构由输入空间、存储空间和输出空间组成,储存空间可分为实际储存空间和虚拟储存空间,可以实现由输入空间到输出空间的映射。CMAC网络结构图如图5所示。
在输入向量量化过程中,输入值根据量化级数激活输入空间的量化子空间,如输入si∈[a,b],可得输入向量量化值为:

图4 单通道力控系统传递函数框图
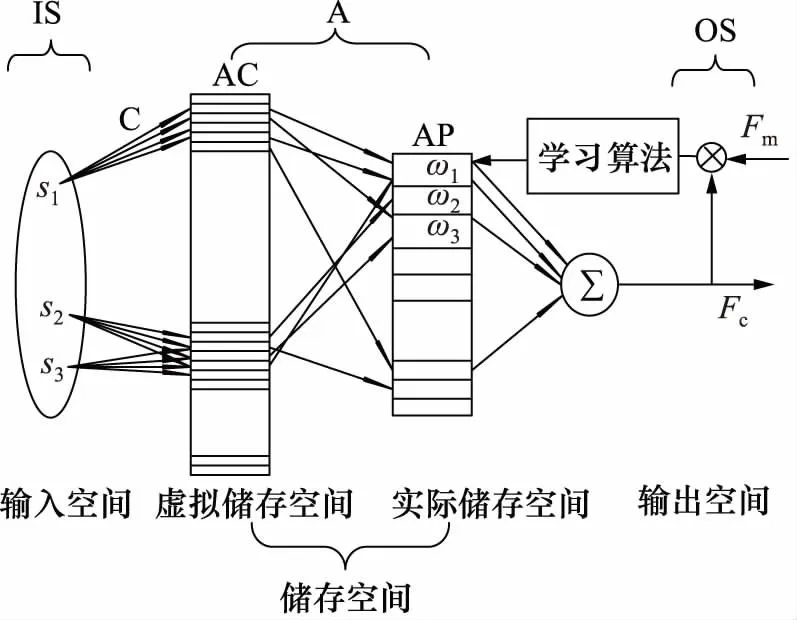
图5 CMAC网络结构图
(22)
式中,smin,smax—— 输入的最小,最大值
M—— 量化级数
在输入空间的输入向量向虚拟存储空间进行映射时,由输入空间的量化子空间激活虚拟存储空间对应储存单元,重叠的虚拟存储空间被激励,映射到虚拟存储空间的输入向量为:
RP=S(uP)=[s1(up),s2(up),…,sc(up)]T
(23)
sj(up)=1,j=1,2,…,c
(24)
式中,c为泛化参数。
由虚拟储存空间向实际储存空间进行映射时,大多采用杂散编码形式,易使多个地址相互重叠。在输入为一维空间的前提下,采用一对一映射方式可以有效提高映射精度。
输出空间输出值为实际储存空间存储单元权值w的加和,输出值为:
(25)
在算法学习过程中,CMAC网络通过最小均方规则对所得权值进行修正,权值调整公式为:
(26)
e(t)=r(t)-y(t)
(27)
式中,r(t) —— 给定信号
y(t) —— 反馈信号
由梯度下降法知,网络权值调整公式为:
(28)
wj(t)=wj(t-1)+Δwj(t)+
α×(wj(t-1)-wj(t-2))
(29)
wj=[w1w2…wc]
(30)
式中,η—— 学习效率
α—— 动量因子
CMAC网格精度与学习效率、动量因子两参数的选择有关,同时随量化级数的增加而提高,量化级数越高所需内存就越大,一般取量化级数M为泛化参数c的10倍及以上,这样才能取得较好的逼近非线性函数的效果。
2.2 CMAC-PID控制器结构设计
CMAC-PID复合控制器采用CMAC做前馈控制[13],可以提高系统的响应速度和控制精度[14-15],用PID控制器保障系统的稳定性,两种控制器结合构成复合控制。其复合控制结构如图6所示。
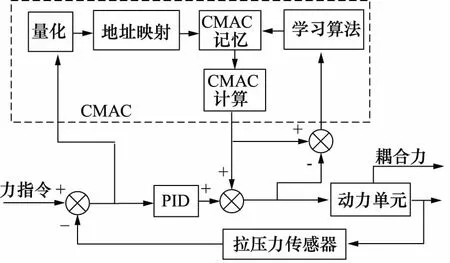
图6 CMAC-PID复合控制器结构图
3 仿真分析
3.1 仿真参数设定
根据多维力系统机构动力学模型、液压动力元件模型及其他环节模型,利用MATLAB/Simulink软件,进行多维力加载系统系统建模,各环节仿真参数见表1。
3.2 静态加载仿真对比分析
对不同控制器作用下多维力加载系统进行静态力、动态力仿真时,首先调节多维力加载系统单通道PID参数,将单通道静态力、动态力响应调至最佳,然后保持PID参数不变,设计CMAC神经网格,进行CMAC-PID复合控制与PID控制下广义空间各力加载通道静态力、动态力加载。
对多维力加载系统进行阶跃力加载仿真时,同时给定Fx,Fy,Fz方向各800 N阶跃力信号。通过仿真,得出CMAC-PID复合控制器与PID控制器作用下仿真曲线对比图,如图7所示。其中,图7a为Fz响应曲线对比图。图7b为Fy响应曲线对比图,图7c为Fx响应曲线对比图,图7d为Mx响应曲线对比图。

表1 多维力加载系统仿真参数
由图7可知,与PID控制器相比,在CMAC-PID复合控制器作用下,Fz,Fy,Fx响应曲线超调量由分别降低了89%,95%,100%,响应时间分别降低了50%,65.7%,15%,由强耦合产生的Mx降低了76.4%。
3.3 动态力加载仿真对比分析
对多维力加载系统进行正弦力加载仿真时,同时给定Fx,Fy,Fz方向各500 N/Hz的正弦力信号。通过仿真,得出CMAC-PID复合控制器与PID控制器作用下仿真曲线对比图,如图8所示。其中,图8a为Fz响应曲线对比图。图8b为Fy响应曲线对比图,图8c为Fx响应曲线对比图,图8d为Mz响应曲线对比图。
由图8可知,与PID控制器相比,在CMAC-PID复合控制器作用下,Fz,Fy,Fx响应曲线幅值衰减分别降低了70.8%,81.1%,86.3%,相位滞后分别降低了41.1%,29.5%,69.5%,由强耦合产生的Mz降低了78.6%。
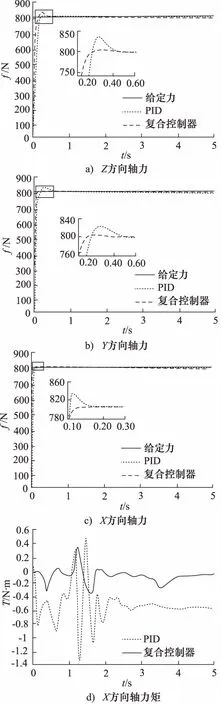
图7 阶跃力加载仿真对比图
4 实验分析
4.1 实验方案
多维力加载系统主体结构实物图如图9所示。多维力加载系统数据采集及控制系统如图10所示。
上位机通过MATLAB/Simulink进行编程,编译后传送至下位机进行实时控制,并且可以用于监控系统的工作状态、接受操作人员的控制指令,控制系统完成实验任务。下位机可以进行实时闭环控制,并且可以将控制信号通过控制板卡输出,其中板卡ACL6126发出-10~10 mA电流信号控制伺服阀,板卡PCI1716可以控制电磁换向阀,当系统出力或关节液压缸出力超过拉压力传感器量程时进行卸荷,起到保护作用。PCI1716也可以采集拉压力传感器信号,并将信号传输给下位机,对液压缸输出力构闭环控制,进而实现液压缸输出力的精确控制。

图8 正弦力加载仿真对比图

图9 多维力加载系统实物照片
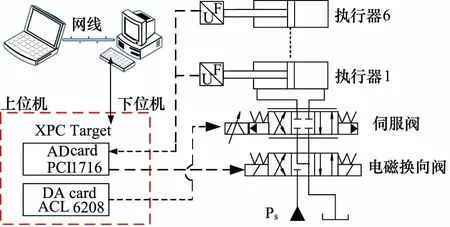
图10 多维力加载系统数据采集及控制系统
4.2 静态力加载实验对比分析
对多维力加载系统进行阶跃力加载实验时,同时给定Fx,Fy,Fz方向各800 N阶跃力信号,其控制器参数调节参照仿真过程。通过实验,得出CMAC-PID复合控制器与PID控制器作用下实验曲线对比图,如图11所示。其中,图11a为Fz响应曲线对比图。图11b为Fy响应曲线对比图,图12c为Fx响应曲线对比图,图11d为Mx响应曲线对比图。
由图11可知,与PID控制器相比,在CMAC-PID复合控制器作用下,Fz,Fy,Fx响应曲线超调量分别下降了39.7%,0,78.6%,响应时间分别下降了42.8%,72.3%,53.6%,稳态误差进一步减小。由强耦合产生的Mx降低了72.2%,下降明显。
4.3 动态力加载实验对比分析
对多维力加载系统进行正弦力加载实验时,同时给定Fx,Fy,Fz方向各500 N/Hz的正弦力信号。由实验可得CMAC-PID复合控制器与PID控制器作用下响应曲线对比图,如图12所示。其中,图12a为Fz响应曲线对比图。图12b为Fy响应曲线对比图,图12c为Fx响应曲线对比图,图12d为Mz响应曲线对比图。
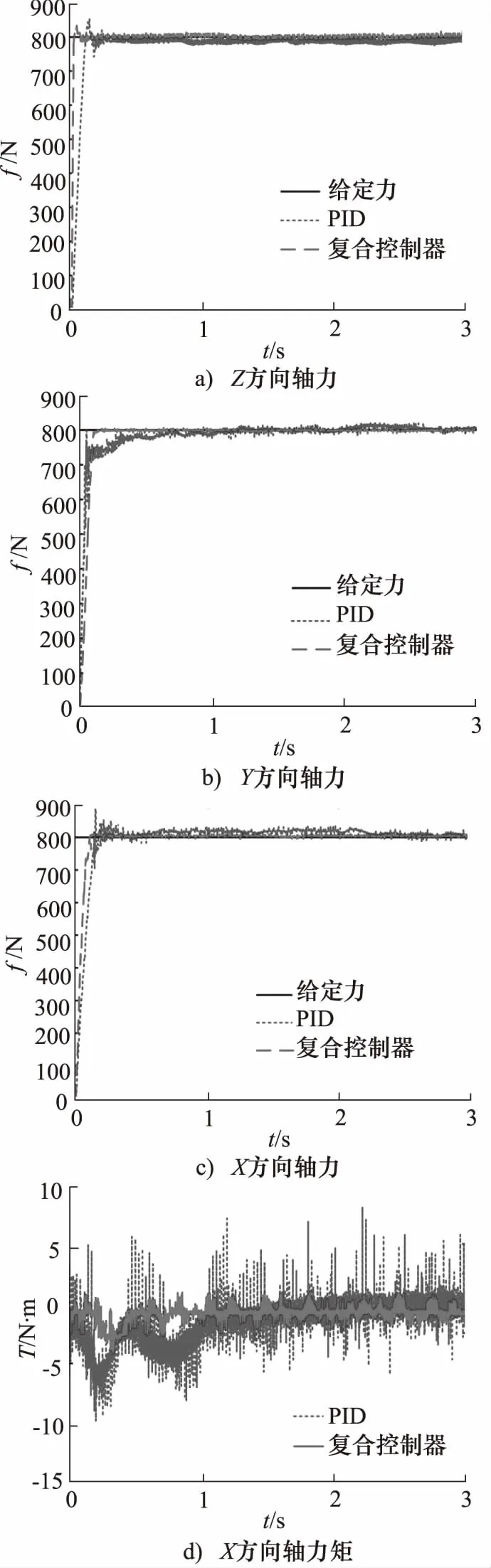
图11 阶跃力加载实验对比图
由图12可知,与PID控制器相比,在CMAC-PID复合控制器作用下,Fz,Fy,Fx响应曲线幅值衰减上分别下降了86.5%,84.9%,86.1%,在相位滞后上分别降低了51.4%,47.1%,35.1%。由耦合力产生的Mz降低了66.6%,且较为稳定。
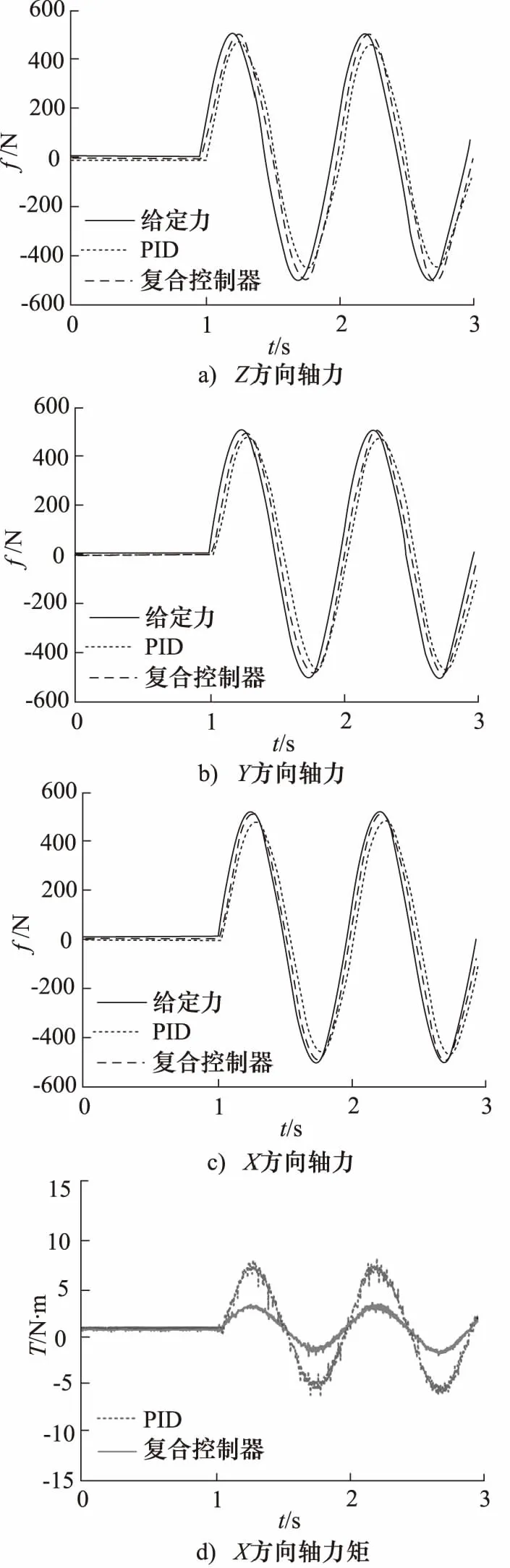
图12 正弦力加载实验对比图
5 结论
(1) 为削弱多维力加载系统通道间强耦合力,同时提高力加载跟随性,引入CMAC控制器,提出CMAC-PID复合控制策略;
(2) 通过多维力加载系统动力学建模,验证了强耦合力的产生原因;
(3) 对多维力加载系统进行仿真和实验研究,研究结果表明:采用静态力加载时,与PID控制器相比CMAC-PID复合控制器作用下稳态误差大幅度减小,系统响应速度、控制精度明显提高,强耦合现象明显改善;采用动态力加载时,正弦力信号响应曲线幅值衰减、相位滞后大幅度减小,由强耦合导致的力冲击现象明显改善。
本研究以液驱并联多维力加载系统为载体,验证了CMAC-PID复合控制策略的有效性,为CMAC-PID复合控制策略在多维力加载环境模拟领域的实际应用奠定基础。
