基于L-K双混沌系统的彩色位级图像加密算法

马 聪 李国东

(新疆财经大学应用数学学院 新疆 乌鲁木齐 830012)

0 引 言

密码学是研究信息安全、通信安全的重要工具，图像加密在互联网的传播安全中起到了重要作用。由于混沌是一种运动轨迹有界、无规律可循的非线性动力学系统，其具有很强的初值敏感性、遍历性、随机性以及难以预测等特点，近几年成为信息保密领域上的重点研究内容[1-3]。季诺然等[4]提出用QR码与混沌序列结合的方法加密图像，将密文图像嵌入到二级Contourlet变换的子带中，能够很好地保护数字图像信息。谢国波等[5]提出了一种基于像素置乱和比特替换的混沌图像加密算法，提高了算法的加密速度，但是算法简单安全性不高。柴秀丽等[6]提出了一种自适应在位级进行操作的加密算法，采用自适应方法加密，提高了算法的安全性。盛苏英等[7]利用耦合映象格子与位级图像相结合并进行逐位扩散，加密算法性能较强，但是不能抵御暴力穷举攻击。Zhang等[8]使用比特级置换的基于混沌的对称图像加密方案，加密安全性高。Zhou等[9]设计了一种利用量子交叉操作和5D超混沌系统的比特级量子彩色图像加密方案。

针对传统加密算法精度有限、安全性不高、加密空间小等不足，本文提出了通过双混沌系统，先对位级进行一次加密，再联合像素级进行二次加密。通过仿真实验表明该算法克服了精度有限、结构单一、加密空间小等问题，具有很高的安全性、抗统计攻击性等优点。

1 理论基础

1.1 Liu混沌

Liu混沌系统是一类含有平方非线性项的混沌系统[10]，其动力学方程如下所示：

(1)

式中：a、b、c为系统参数，h、k为控制参数。当满足条件a=10、b=40、c=2.5，k=1、h=4时系统表现出混沌行为。为了增加密钥空间的复杂性，消除混沌序列的随机性，Liu混沌映射初值采用随机选取的方法，将一维Logistic映射迭代1 000次，在1 000次以内随机选取三个值作为Liu混沌映射的初值，选取结果为x0=0.797 6、y0=0.311 4、z0=0.488 3。一个混沌系统的奇异吸引子在相空间是整体有界的，Liu混沌系统的奇异吸引子是一类具有无穷嵌套层次的自相似几何结构。经过20 000次迭代后的奇异吸引子和相位图如图1所示。

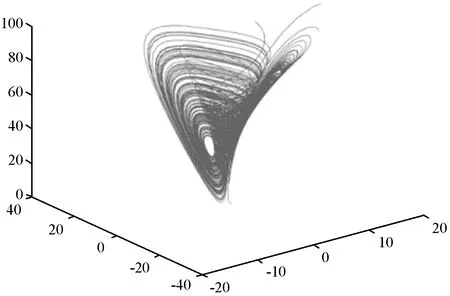
(a) 奇异吸引子

(b) x-y平面

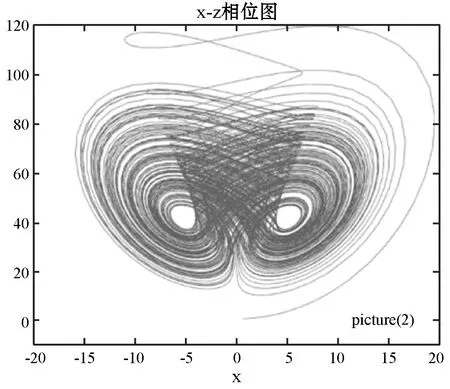
(c) x-z平面

(d) y-z平面图1 Liu混沌奇异吸引子及相位图

1.2 Kawakami超混沌

超混沌系统的动力学具有更加随机、相空间更大等优势，将混沌运用在加密体统中能有效地提高加密性能。Kawakami超混沌是1979年由Kawakami和Kobayashi提出的首个研究自同态的模型，Kawakami映射的动力学表达式如下：

(2)

式中：c、d为控制参数。c=0.1、d=1.6时系统处于超混沌状态，Kawakami超混沌的初值选取一维Chebyshev迭代1 000次以内的两个随机数，x1=0.401 3,y1=0.100 7，Kawakami超混沌迭代1 500次的奇异吸引子如图2所示。

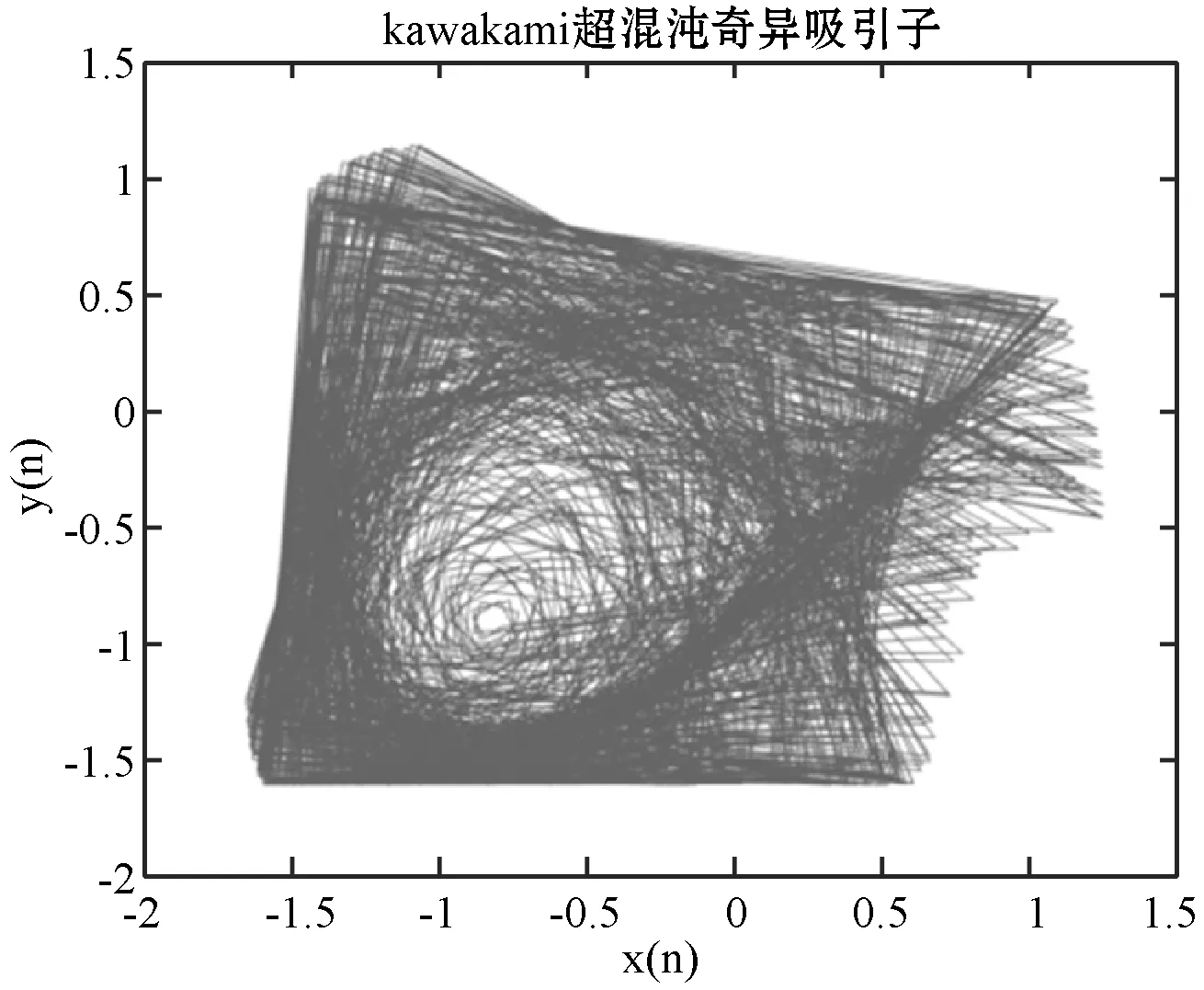
图2 Kawakami超混沌奇异吸引子

2 L-K双混沌系统的彩色图像加密算法

加密算法流程如图3所示。

图3 加密算法流程图

加密算法采用置乱-扩散-置乱-扩散的结构，首先将明文图像转换为R、G、B三个通道，将三通道中每个像素值分别进行二进制转换，这时每一个通道可以看作是由8个m×n的0和1序列组成的矩阵，即R(x,y)={R1(x,y),R2(x,y),…,R8(x,y)},不同位平面包含的信息量不同[11]，如表1所示。

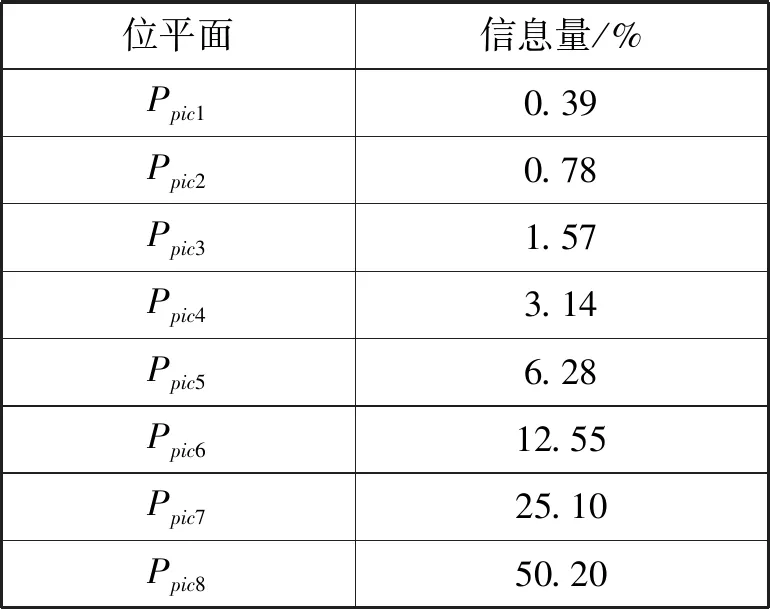
表1 不同位平面信息量

由表1可以看出，高三位包含了主要的图像信息，位数越低，所包含的信息量越少，因此将高三位的每一位单独作为一个加密图像，将低五位的位平面向左移位异或构成一个加密图像，采用低五位和高三位分别置乱、交融扩散的方式进行第一轮加密。同时为了消除不同层之间的相关性，进行了第二轮置乱-扩散操作。

1) 一次置乱-扩散算法。

按照浮点算法将3×m×n的彩色图像分为大小m×n的R层、G层、B层图像。

以R层的加密过程为例，将R层分解为8个位平面，鉴于高三位包含了主要的图像信息，因此将高三位分别单独作为一个平面，从高到低记为pic1、pic2、pic3，将低五位如式(3)所示方式向左移位异或合成一个位平面，记为pic4。

pic4(i,j)=P5(i,j)⊕P4(i,j)⊕P3(i,j)⊕

P2(i,j)⊕P1(i,j)

(3)

向左移位异或程序如下：

Bit4=WW(:,:,4);

%WW是Matlab读取的图像信息

Bit5=WW(:,:,5);

P1=bitxor(Bit5,Bit4);

P2=bitxor(P1,Bit3);

P3=bitxor(P2,Bit2);

P4=bitxor(P3,Bit1)。

步骤1将初值为k1的Logistic模型迭代k2次选取三个值作为Liu混沌系统的初值，并设置Liu混沌系统的参数。为了消除暂态效应，迭代S+1 000(S>m×n)次选取中间S个不重复的值，在S中截取三段m×n的混沌序列，得到序列xi、yi、zi。

步骤2采用Arnold置乱[12]k3次实现pic1-pic3的像素值位置变换，Arnold置乱思想是在矩阵中先做x轴方向的错切变换，再做y轴方向的错切变换，反复拉伸折叠；接着采用光栅扫描的方式将pic4变换成一维向量，对pic4位级采用索引位置置乱混淆的像素值位置，在S中任意截取m×n个的混沌序列构成一维向量，按降序排序，得到的序列为si={sm×n,sm×n-1,…,s1} ，并记录原序列在si中的位置为Tsi={Ts1,Ts2,…，Tsm×n}，按此位置对原序列进行变换，此时得到一个新的一维向量，转换成m×n矩阵即完成位级置乱。

步骤3将已经加密的高三位Pici(i=1,2,3)分别进行像素值求和得到sumIi，采用低五位pic4加密高三位的混淆扩散方式，对混沌序列按照式(4)进行标准化处理，迭代m次，得到m个混沌序列。

xi=floor(mod(xi×1014),256)yi=floor(mod(yi×1014),256)zi=floor(mod(zi×1014),256)

(4)

按照式(5)进行自适应扩散操作，Pic′(3)、Pic′(2)、Pic′(1)分别是xi,yi,zi的高三位。

(5)

然后，计算三个异或矩阵分别按位相加的结果，按照式(6)得到R层密文图像。

R′=(min+middle+max)mod 2

(6)

步骤4G层、B层采用相同的方法分别加密，再按循环异或得到最终密文图像，循环异或的函数为BitCircShift(A,k,m)。

C=R′⊕G′⊕B′

(7)

2) 二次置乱-扩散算法。

第一轮加密过程是基于位级层面进行像素值替代和扩散，为了消除层之间的相关性，增强加密算法的安全性，改进第一轮密文产生的像素值，在灰度图像上进行第二轮加密。

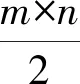
C1=mod(ceil(abs(x1i+y2i)×105)+C,256)

(8)

步骤2对所生成的超混沌序列进行取余操作，新的混沌序列结合密文图像像素值信息，使超混沌序列更具有随机性，改进方法如式(9)所示,

xi=mod(floor((sum(C1)/abs(xi))×106),256)yi=mod(floor((sum(C1)/abs(yi))×106),256)

(9)

步骤3采用Hilbert曲线对第一轮加密的密文图像进行置乱，Hilbert曲线的思想是把一个方阵矩阵分成4个小方阵，依次从左下角的中心出发向上移动到左上角的中心，再向右扫描到右上角的中心，向下到右下角的中心，按此顺序不断迭代扫描，直到遍历整个方阵,置乱示意图如图4所示。

图4 Hilbert置乱示意图

步骤4将Hilbert置乱后的图像记为Q，在扩散加密操作中，将图像纵向分为两半Q1、Q2，两半同时展开加密，最后合并得到完全扩散的密文图像。

(10)

3) 为了达到加密图像充分混淆的目的，重复步骤1)-步骤2)T次，T作为密钥保存，至此完成加密过程。

3 仿真实验

实验选用加密的经典图像Lena为对象，Lena图像的分辨率为256×256，大小为192 KB。采用Win10系统在MATLAB 2018b的环境下对该算法进行仿真，其中，Liu混沌的系统参数设置为a=10、b=40、c=2.5、k=1、h=4，Liu混沌映射的初始值为x0=0.797 6、y0=0.311 4、z0=0.488 3，Kawakami超混沌的系统参数设置为c=0.1、d=1.6，初值为x1=0.401 3、y1=0.100 7。除了上述密钥之外，本文算法的其余密钥为S=92 463、k1=0.3、k2=1 000、k3=99、k4=0.75、k5=999、T=5，仿真实验结果如图5所示。为了说明本文算法加密的实用性，使用分辨率为512×512，大小为1 MB的电子发票为例，在同样的操作环境下，使用相同的系统参数和系统初值进行加密，结果如图6所示。

(a) 明文图像 (b) 密文图像 (c) 解密图像图5 仿真实验结果

(a) 明文图像 (b) 密文图像 (c) 解密图像图6 电子发票加密

4 安全性分析

4.1 置乱度分析

置乱度是衡量像素值位置变化杂乱程度的重要指标，置乱度越大，说明图像混淆的越乱，攻击者不能识别真实内容，因此图像更加不易被破解，置乱度的取值范围为SM∈(0,1)，置乱度的数学表达如下：

(11)

X={xij}m×n表示明文图像，Y={yij}m×n表示密文图像，R={rij}m×n表示与明文图像大小相同的随机分布图像，选取最终密文图像进行置乱度分析，用本文算法得到的置乱度为0.992 8，接近1，说明本文算法的置乱效果很好，图像信息的安全性更高。

4.2 直方图分析

直方图分析结果如图7所示，可以看出，明文图像像素值分布参差不齐，而密文图像像素值频率分布比较均匀，难以找出原始图像的规律，说明加密后的密文图像对穷举攻击有很好的抵抗作用。

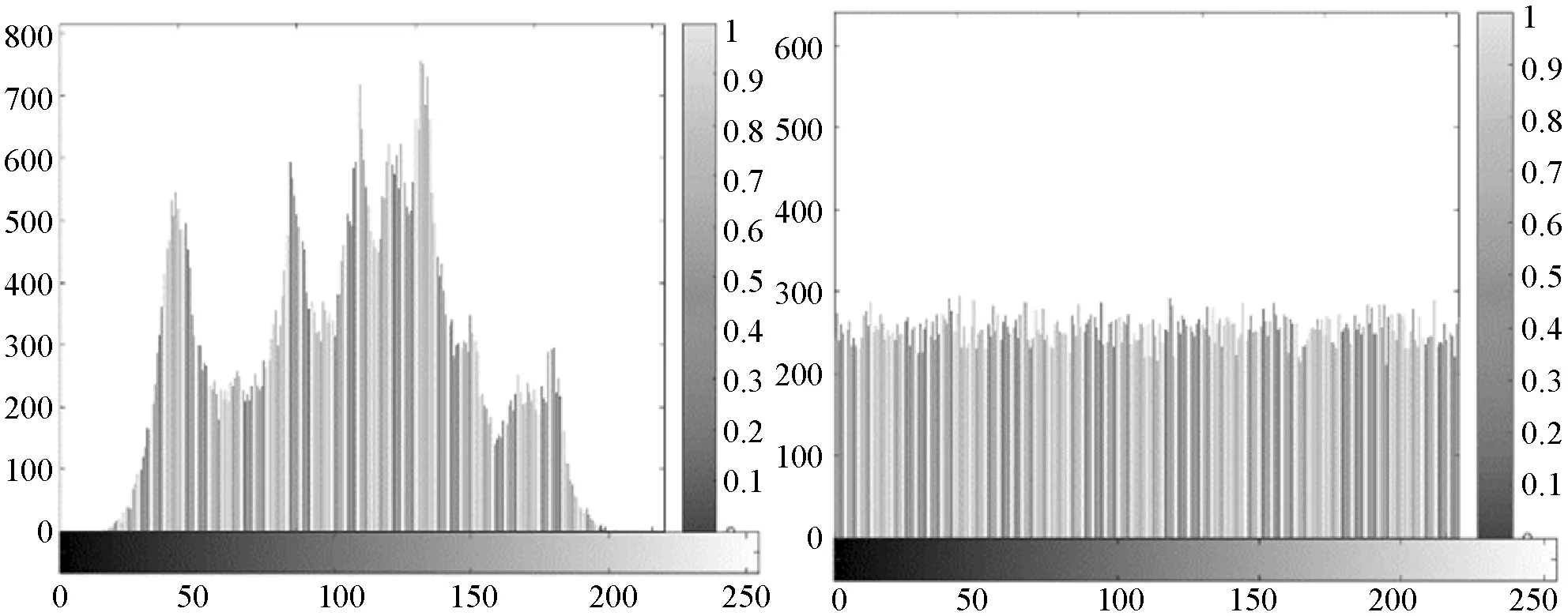
(a) 明文图像直方图 (b) 密文图像直方图图7 明文和密文图像直方图

4.3 密钥空间及密钥敏感性分析

彩色图像信息包含的数据信息量大，若密钥选取的较少，则无法满足安全性，密钥空间越大，密钥长度就越长，密文图像更能有效地抵御穷举攻击，密钥是传递者和接受者的媒介，将加密算法中的密钥传送给信息接受者，接受者就能根据密钥还原出原始信息。本文算法的密钥空间为1016×19=10304，密钥长度为log2(10304)，远大于128 bit，可见密钥空间很大，足以抵御穷举攻击。

本文的加密算法对密钥的依赖性非常强，在解密过程中，密钥微小的变化都不能得到正确的解密图像，对Liu混沌系统和Kawakami超混沌系统的初值进行2×10-14的微小变动时，即x0=0.797 6+2×10-14，x1=0.401 3+2×10-14，所得解密结果如图8所示。

(a) 错误解密(b) 错误解密 (c) 正确解密图8 敏感性测试

4.4 明文敏感性分析

像素变化比率(简称：NPCR)显示的是不同像素点个数占全部像素点的比例，表明当明文中有一个像素值发生变化时密文图像中像素值变化的比率，NPCR越接近100%，说明明文像素值的微小变动都会大幅改变密文信息。D1表示密文，D2表示明文，公式如下：

(12)

归一化平均改变强度(简称：UACI)显示的是两幅图像全部相应位置像素点的差值和最大差值的比值的平均值。UACI的理想值是接近 33.463 5%，这时对明文的细微改变敏感性强烈，计算公式如下：

(13)

对明文图像中任意一点像素值(100,101)进行微小变动为(101,101)，此时NPCR和UACI分别为99.78%和33.37%，均非常接近理想值，对比文献[13]和文献[14]，结果如表2所示。

表2 NPCR和UACI值

4.5 相邻像素相关性分析

在一幅图像中，其像素值之间存在一定的相关性，根据式(14)，截取1 000对像素点(x,y)进行分析，计算结果如表3和图9所示。可以看出，明文图像相邻像素的相关性比较高，呈现出明显的线性相关性，相关系数接近1，而密文图像各方向像素之间相关系数均在0左右，说明本文加密算法达到了理想效果。

(14)

式中:

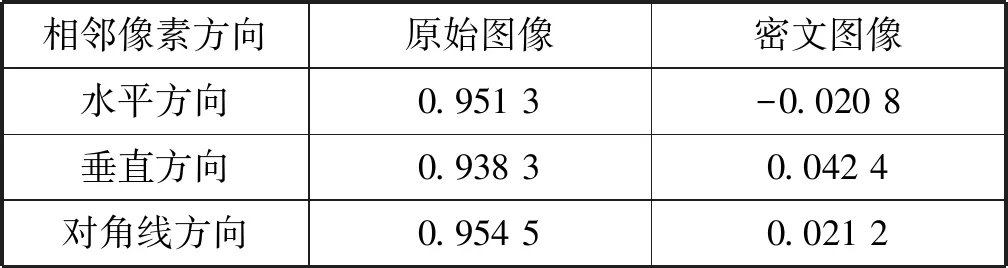
表3 明文和密文图像相邻像素间相关系数

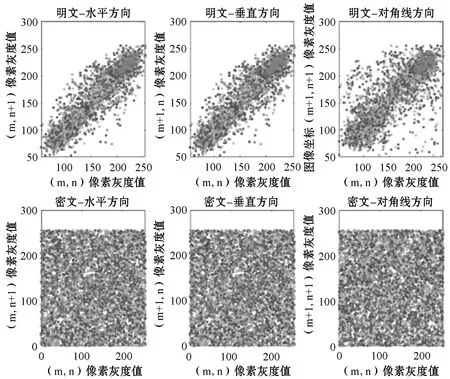
图9 明文和密文图像相邻像素相关性

4.6 信息熵分析

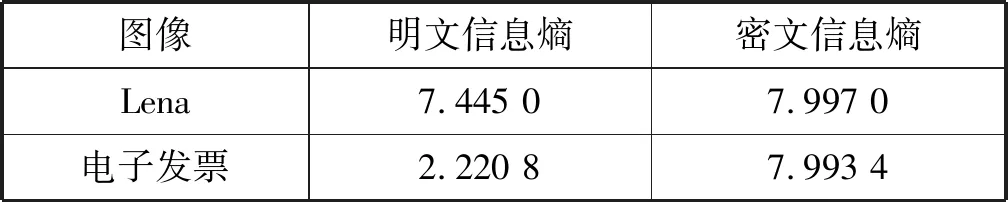
根据Shannon定理[15-16]信息熵的理论，信息熵反应了一个序列的随机性，信息熵越大，随机性越强，灰度值分布越均匀。当图像中各灰度值出现的概率相等时，图像的信息熵最大，256个灰度级的灰度图像信息熵的理想值为8。为了体现本文算法的优越性，对Lena图像与电子发票的明文与密文信息熵进行对比，根据式(15)计算信息熵的结果见表4。可以看出，经过本文算法加密的图像信息熵都非常接近理想值，表明本文算法能够有效地抵御穷举攻击，加密效果很好。

(15)

5 结 语

本文将混沌理论用于图像加密领域，该算法主要特点是：先将Liu混沌系统用于位级图像，所得到的加密图像作为下一轮加密的载体，第二轮改进密文图像为像素级，并将Kawakami超混沌系统用于像素级加密，采用置乱-扩散-置乱-扩散的结构，分别在位级平面和像素级平面进行加密。实验结果表明，该算法能很好地抵御各种暴力攻击，密钥空间大，加密算法的安全性高，并且该算法解决了混沌加密的单一性，提高了加密的实时性，加密效果较好，在网络安全、信息传输、移动支付等方面具有广阔应用前景。