基于兴趣相似度传递的增强LSH统计预测算法
2020-03-13夏小娜
夏小娜 邹 麒
1(曲阜师范大学统计学院 山东 曲阜 273165)2(曲阜师范大学信息科学与工程学院 山东 日照 276826)
0 引 言
个性化推荐是大数据和在线应用的关键技术。通过捕捉用户的行为偏好与目标需求,自主为用户提供合适的服务。这里涉及两个需求背景:一是用户知道自己需要的具体是什么,二是用户并不知道。这两方面都需要有效的推荐策略。推荐时需要综合考虑用户自身的潜在需求,也要考虑受邻近用户的影响。但无论是面对怎样的需求背景,当大量的服务结果呈现在用户面前时,用户并不能客观评估排序潜在的大量可供选择的服务。基于统计预测的推荐策略帮助用户从海量候选结果中提供有用和有效的建议,或者做有意义的引导和启发。
协同过滤是实现个性化统计、预测和推荐常用的方法之一,它对群体进行搜索,从中找出与用户兴趣偏好近似的其他用户作为“兴趣近邻”,对近邻所偏好的相关内容进行分析和考察,将它们组合起来,计算近似度和推荐权重,构造出排序的候选列表[1]。
在对大数据集进行分析并生成推荐列表时,基于物品的过滤推荐方法明显要比基于用户的更快,但存在维护物品相似度表的额外开销。基于物品的推荐和基于用户的推荐,对于数据集的稀疏性处理存在差异,但算法的本质是类似的[2-3],在搜索邻近用户时,以基于用户或物品的相似度为基础,所实现的推荐效果取决于相似度度量的准确性和有效性,以及关于相似度空间搜索和计算过程的能力。邻近用户的“邻近”体现为用户间关于目标的近似选择,以此所体现的近似兴趣偏好,是围绕用户兴趣借助算法实现的用户邻近域界定,即为“兴趣近邻”[4-5]。
有关在线平台的服务推荐,无论是基于用户的推荐还是基于物品的推荐,相关的评分向量都是高维的,在高维数据空间中做到快速地定位相似的用户或者物品,一般情况下有两种解决思路:最近邻域检索和近似最近邻检索。因检索过程是个NP问题,因此通常采取近似最近邻方式。LSH(Locality-Sensitive Hash)[6]就是其中有效的研究方法。LSH的含义表征为将高维空间中邻近的点HASH映射到低维空间后仍距离较近,原本较远的点映射后仍具有较远的距离[7]。本文改进LSH应用模型,充分计算用户需求域的邻近关联信息,结合用户自身的潜在偏好趋向,构造自主的统计预测机制,设计了ILSH算法。
1 相关工作
基于分布式敏感哈希,设计隐私保护和可拓展的服务推荐方法[8]。有效降低实时推荐的运算复杂度,提高评分数据在高维空间中的相似性查询效率;通过运用两个LSH策略分类高维数据[13],加入增量聚类算法,批量合并相似度矩阵以合并离线聚类算法;LSH两级结构可以提高检索效率[15],将提取的特征外包给云服务器还需要做深入的研究,以便于减轻数据所有者和数据用户的负担;进一步,使得LSH用于视频的异常检测方法[17],将正常活动散列到多个特征桶中,过滤异常活动,以此实现在线更新程序融入适应视频场景变化的LSH框架。
基于邻近搜索机制,可实现多对象优化算法和局部敏感哈希的协同,解决“一对多”“多对一”动态选择和传递问题[9-10]。利用LSH发现真正感兴趣的事件,加快集群发现过程,保持聚类质量[11]。但该方法并没有应用于多个社交媒体数据集,无法比较同一事件在多个平台的效果,方法还需要充分检验以扩展到更复杂的情形。
LSH在Web服务中也得到了有效运用。针对Map-Reduce中聚类大规模数据集时的有效分布式密度峰值问题[12],设计LSH进化算法,以支持用户指定所期望的近似准确度,减少清洗数据和计算消耗;设计基于MapReduce编程模型的LSH并行集合相似度关联方法,可以减少计算相似度时需求比较的次数;实现LSH在WoS(Web of Science)和Scopus匹配中的应用[16],实现检测精确匹配,利于衡量高频数据的重叠情况。
SLH已得到了广泛应用,许多有关SLH的研究,多半是局限于某一领域或者特定数据集参数的调优,或者直接用于部分数据的处理[18],并没有从SLH数据结构和算法流程上进行调整和改进,在应用过程中,同样也带来了其他没有解决的问题。
SLH已得到了广泛应用,许多有关SLH的研究,多半是局限于某一领域或者特定数据集参数的调优,或者直接用于部分数据的处理[18],并没有从SLH数据结构和算法流程上进行调整和改进,在应用过程中,同样也带来了其他没有解决的问题。本文从SLH设计结构出发,扩展优化算法,在提高统计预测运算效率的前提下,提高兴趣相似度的有效传递。
2 局部敏感哈希
2.1 基本定义
定义1敏感的函数族
给定一族哈希函数,是一个从欧式空间到哈希编码空间的映射。如果以下两个条件都满足,则称此哈希函数为敏感的函数族[12]。
(1) 若p∈B(q,r1),则PrH[h(q)=h(p)]≥p1;
(2) 若p∉B(q,r2),则PrH[h(q)=h(p)]≤p2。
定义中B表示的是以q为中心,r1或r2为半径的空间,图1是该定义的坐标系分布描述。
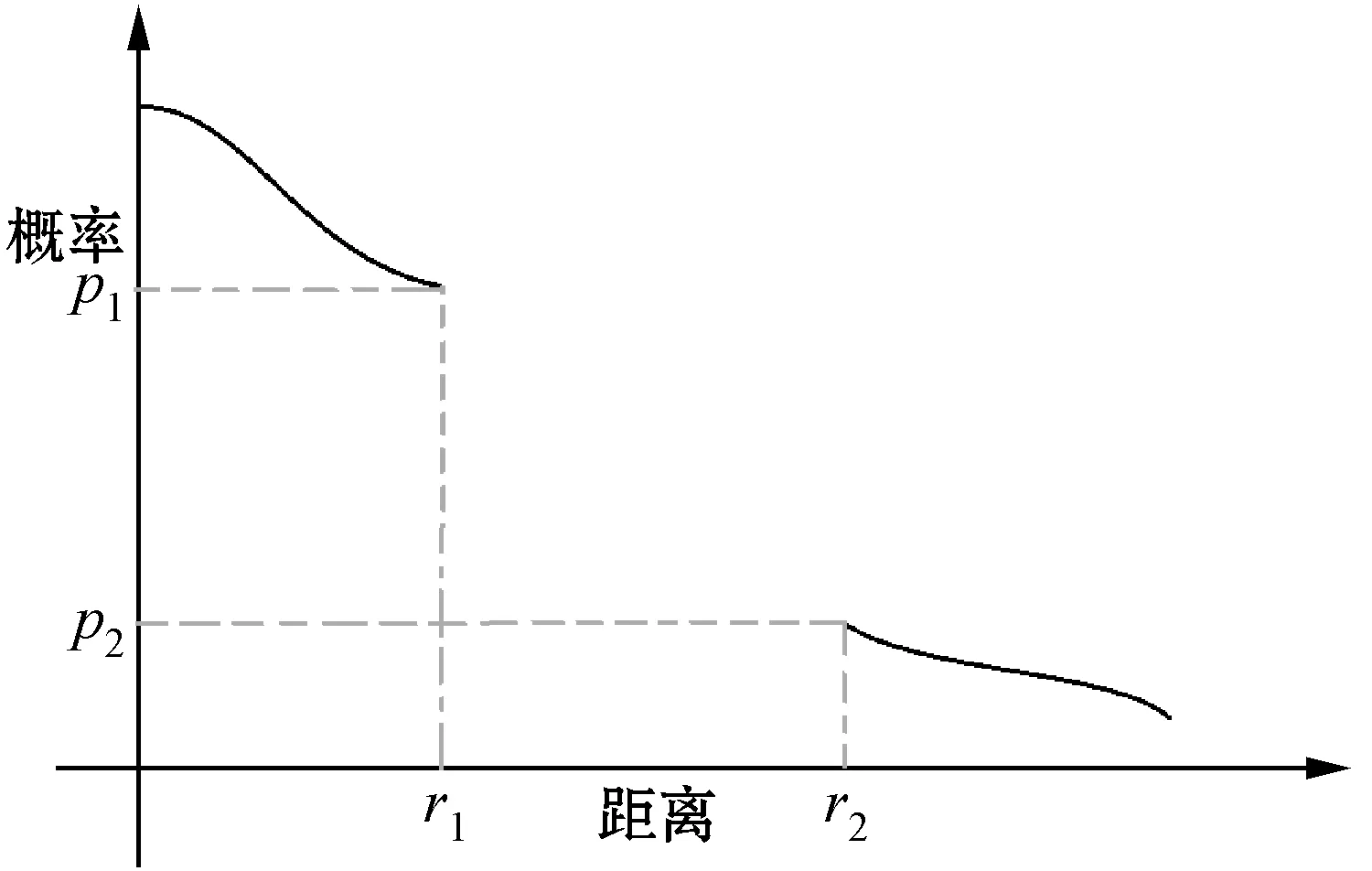
图1 定义1图例
定义2给定数据集S及相关的局部敏感哈希族x,y∈S,若数据对象x,y∈S成立,应满足定义为[13]:
Ph∈H[h(x)=h(y)]=sim(x,y)
(1)
上述两种定义的定义角度不同使得这两种定义在形式上差距很大,但是本质上是一致的,即越相近的数据对象发生哈希冲突的概率越高。
2.2 基本思想
在进行预测推荐时,无论是user-base还是item-base,预测过程的相似度计算其本质都是基于物品的评分向量,由用户和评分形成矩阵,具有高维的特点。要实现快速寻求相似的用户或者物品,需要围绕用户或者物品进行近邻检索。
LSH的核心理念是通过一组哈希函数,把相似的数据对象哈希到相同的哈希桶中,越相似的对象被哈希到相同桶中的概率越高。这些桶中的数据对象构成目标候选集,从而过滤掉大量的相似概率很低的数据对象。
一般情况下,使用HASH技术有效避免冲突,如使用HashTable实现与Redis的一致性哈希过程。若经过Hashing后,两组数据具有相同的HASH VALUE,则LSH认为同两对象是具有相似性的。这样,对每一次近似近邻的查询过程只需要对待检测的对象进行同样的哈希过程,直接从对应的HASH VALUE特征桶中找到相似的对象。
建立一个哈希函数族,每个函数随机生成不同的边界,边界之间形成区域。每个函数进行向量运算,生成一条有向线,如图2所示,这些有向线的集合即是哈希族。生成有向线的条数是穷举过程,目的是找到一个合适的位置,最终被圈在同一区域的点将视为相邻的。

图2 LSH算法思想的几何图形解释
LSH运算快,可以跨平台实现合作推荐,而不破坏用户的隐私。但LSH随机分域过程也可能存在错误。解决这个问题有两个思路:一是使用多个独立的哈希表,进行多次区域分割;二是推荐前的多检索策略,对于每一次检索进行评分预测,求取平均。
2.3 增强局部敏感哈希
局部敏感哈希的定义中不难看出,LSH虽然是近似最优技术,但是并不能保证计算结果的精确性,通过LSH我们能得到一个或多个Hash表,一次哈希会有很大的可能性将非相似的数据哈希到相同的哈希桶中,这种将非相似数据对象哈希到相同哈希桶中的情形称为纳伪(False Positive)。同时未将真正相似的对象哈希到相同哈希桶中的情形称为拒真(False Negative)。为了保证局部敏感哈希的查询质量,需要尽量降低False Positive和False Negative,也就是实现LSH的增强。常用的增强LSH的方法有使用多个独立的哈希表,运用AND、OR、XOR等操作以及这些操作的级联运算。
增强局部敏感哈希的执行过程体现为:
输入: “user-item”评分记录,pool_size代表每个哈希表所对应哈希函数的个数,hash_count是哈希表的个数。
输出: 具有hash_count个数目的哈希索引结构。
过程:
Step1算法初始化。将“user-item”评分记录转换为“user-item”评分矩阵,具有m个用户、n个项目的评分矩阵Dm×n表征为:
对于一个用户,其评分记录可以表示为向量uk=(itemk,1.q,itemk,2.q,…,itemk,m.q),其中itemk,l.q(1≤l≤n,1≤k≤m)表示用户k对于物品的评分,若该用户从未评议过该项目则该评分为0。
Step2LSH构造。对于每个用户u∈U,根据既定的哈希函数族{hk(u)}将评分记录向量uk映射到哈希空间中。hk(u)计算公式表示为:
(2)
式中:v是一个m维向量(v1,v2,…,vm),(1≤i≤m),其中vi的取值范围为[-1,1],运算符∘表示对两个向量进行点积运算。
对于式(2)可以用一下物理模型进行描述:
向量v是一个对高维空间进行分割的超平面,LSH的过程即是将分布在高维评分空间中的用户评分点集进行区域划分,基于前文中关于LSH基本思想的阐述,如果两个点相似,则会有极高的概率被超平面划分到同一个区域当中。
Step 3LSH索引构建。对于Dm×n中的每一个评分向量uk=(itemk,1.q,itemk,2.q,…,itemk,m.q),利用哈希函数进行映射,并对每个哈希表进行分桶构建索引。
Step 4用户的兴趣相似性检索。有关用户的兴趣相似性检索,只需将hash_count个哈希表中处于一个桶中的所有用户的并集作为待预测目标用户的兴趣最近邻集合。在此基础上,运用上述三步,计算目标最邻近用户的在线哈希族函数个数N,找到规模等于N的哈希桶,将用户作为相似的候选“近邻”放进哈希桶。
3 ILSH统计预测算法
现实中的推荐系统的物品远远多于用户,而对于单个用户而言,其评分向量往往是极其稀疏的。单纯通过LSH算法找到目标用户的相似用户进而对所有物品进行无差别的加权相加预测评分,并没有考虑到用户会对特定的产品存在一定的爱好偏差这一基本消费心理。因此,本文的ILSH只将相似用户对相似物品进行平均加权取值,用以描述用户对特定物品的爱好偏差。
设定待预测目标用户u的最近邻集合表示为U,目标物品i的最近邻集合为I,Rvi是近邻用户v对物品i的评分,则用户u对i的预测评分为:
(3)
基于改进LSH(后文用ILSH表示)的统计预测算法主要分为四个步骤,伪码描述如算法1-算法4。
算法1构建LSH-family
Hash_count: 哈希表的个数
Pool_size: 每个哈希表中哈希函数的个数,即哈希值
Dimensions: 评分向量维度
H(·): LSH函数族
Fork=1toHash_count
Forg=1topool_size
Forl=1toDimensions
Pkgl=random[-1,1]
EndFor
vk=(Pkg1,Pkg2,…,Pkgdimensions)
EndFor
Hk=(v1,v2,…,vpool_size)
EndFor
算法2分别对user和item构建索引
u(j):用户j的评分向量
i(k):物品k的评分向量
Hu(·):根据用户评分向量建立的LSH-family
Hi(·):根据物品评分向量建立的LSH-family
Users:用户列表
Items:为物品列表
/*根据用户评分向量和物品评分向量建立不同
维度的LSH-family和哈希表*/
Foru(j)inUsers
Hj(u(j))=(v1·u(j),v2·u(j),…)
Ubucket[Hj(u(j))]·append(userj)
Fori(k)inItems
Hk(i(k))=(v1·i(k),v2·i(k),…)
Ibucket[Hk(i(k))]·append(itemk)
算法3相似性检索
Utarget: 目标用户
Itarget: 目标物品
Forx=1toHash_count
hvu=Hu(Utarget)
uset+=Ubucke[hvu]
EndFor
Fory=1toHash_count
hvi=Hi(Itarget)
Iset+=Ibucket[hvi]
Endfor
EndFor
算法4统计预测评分
similar_ratings=rating[uset,:]
similar_ratings=similar_ratings[:,Iset]
p_rating=similar_ratings
[similar_ratings.nonzero()]mean()
4 实 验
4.1 训练数据集及评价指标
ILSH算法的实验数据集选自University of Minnesota的GroupLens课题组提供MovieLens(http://grouplens.org/datasets/movielens/),涉及6 040个用户关于3 706部电影的评议投票,共包括1 000 000个评分记录,设定电影的评分数值分布在区间[0, 5]。评分越高,则表明某用户对某电影的兴趣偏好度越大。
有关用户的评分统计度量标准定位于平均绝对误差(Mean Absolute Error, MAE),通过计算兴趣偏好近似用户的评分与待评估的目标用户评分之间的偏差,根据此偏差大小预测准确性。平均绝对误差的数值越小,推荐准确性越高。假设待预测的用户评分表示为向量表达式p=(p1,p2,…,pm),实际的用户评分向量为r=(r1,r2,…,rm),则平均绝对误差为:
(4)
4.2 实验设计及结果分析
4.2.1pool_size和hash_count的选择
为了提高哈希的查询质量,尽量降低False Positive和False Negative,在实施中,通常会采用两种策略[14]:
(1) 在一个Hash表内使用更多的哈希函数;
(2) 建立多个Hash表。
本文实验主要考察pool_size和hash_count两个参数对实验结果的影响,训练过程如图3-图5所示。用PYTHON实现本文算法,从实验数据的训练结果中可以看出,当相关参数值分别设定为pool_size=7, hash_count=12, 所得到的MAE结果值最低,也是最好的实验结果。通过取不同的参数值训练数据可以看出,对于兴趣度相似或近似的用户,可以取得更好的检索准确率,从而确保较高的目标服务推荐质量,提高用户的满意度。
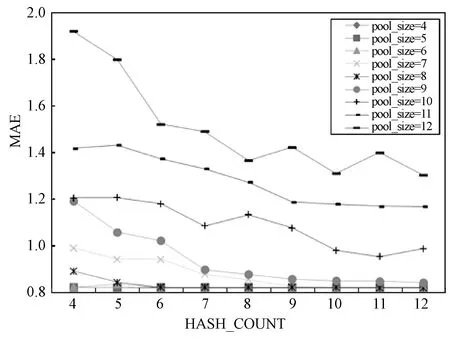
图3 不同参数对MAE的影响

图4 不同参数对MAE的影响
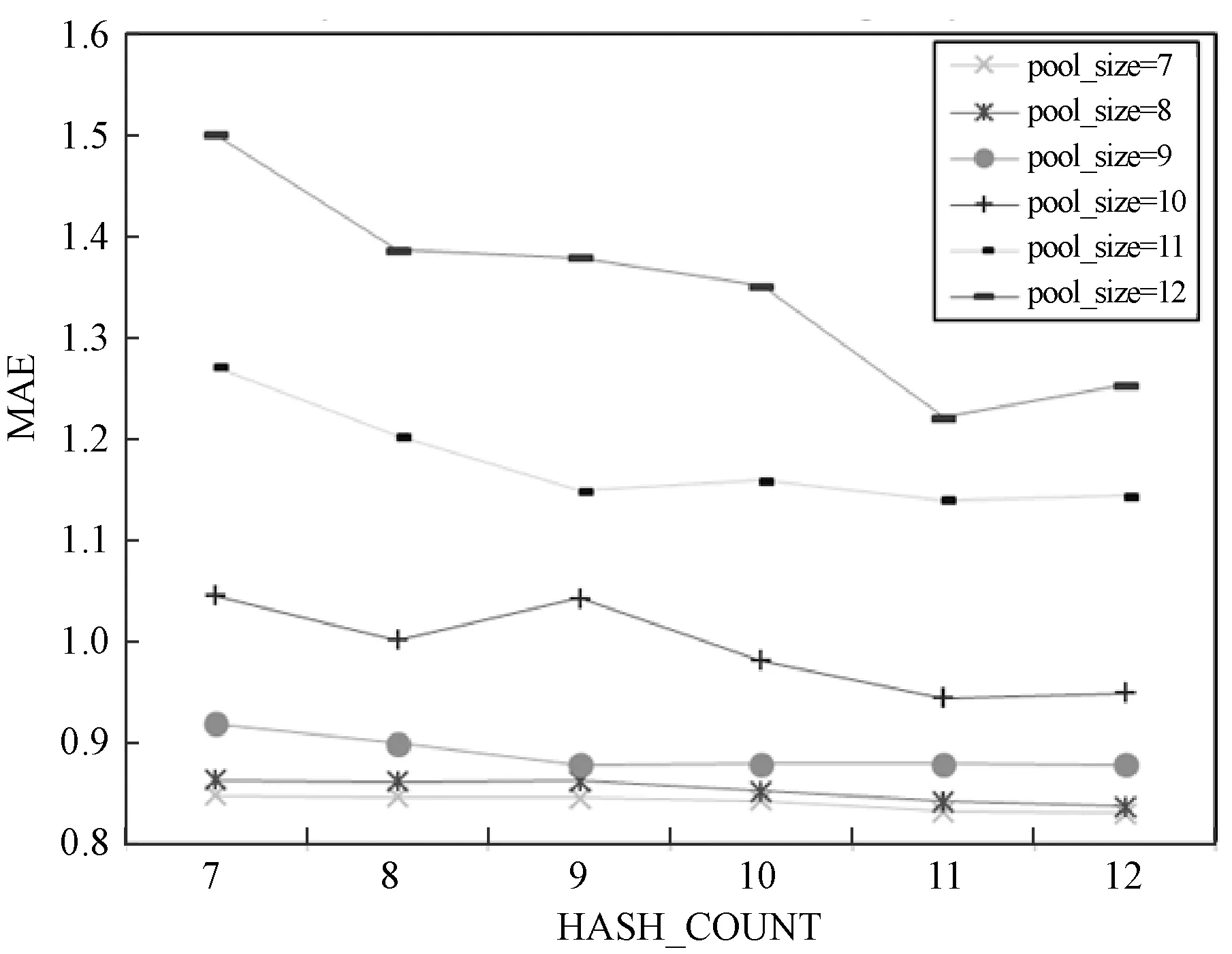
图5 不同参数对MAE的影响
4.2.2与传统基于用户/物品的协同过滤算法的对比
为检验ILSH算法的优势,在算法训练中,我们划定不同用户评分的稀疏数据矩阵展开针对性检验。稀疏数据并非无用数据,数据的稀疏度指的是不存在数据的多维结构的单元的相对百分比,在数据稀疏的前提下从多维结构中能否学习并挖掘出更多有效数据,是算法的一个重要衡量指标。这里我们设定稀疏度计量区间为[0.100,0.300],步长为0.025,在近似用户评分矩阵的删除数据比例上,比较用户评分矩阵的稀疏度所实现的数据获取效果,即对比本文提出的ILSH与传统的基于用户PCC(User-based Pearson Correlation Coefficient, UPCC)的协同过滤算法和基于物品(Item-based Peason Correlation Coefficient, IPCC)的协同过滤算法的MAE值。根据4.2.1节的实验结果,设定hash_count=12,pool_size=7。
实验结果如图6所示,当数据稀疏度逐渐上升时,UPCC、IPCC、ILSH的MAE都会有一定程度的上升,但本文提出的ILSH算法的MAE一直处于较小的水平,且比传统的UPCC和IPCC的MAE低很多。

图6 UPCC、IPCC、ILSH的MAE随着 数据稀疏度变化的对比
4.2.3ILSH与最新LSH改进算法的比较
为将ILSH同最新LSH算法的执行结果进行有效比较,采用了与4.2.1节相同的实验方案,选取不同的用户评分矩阵稀疏度,比较用户评分矩阵在不同的稀疏度下两种算法的MAE,实验对比结果如图7所示。
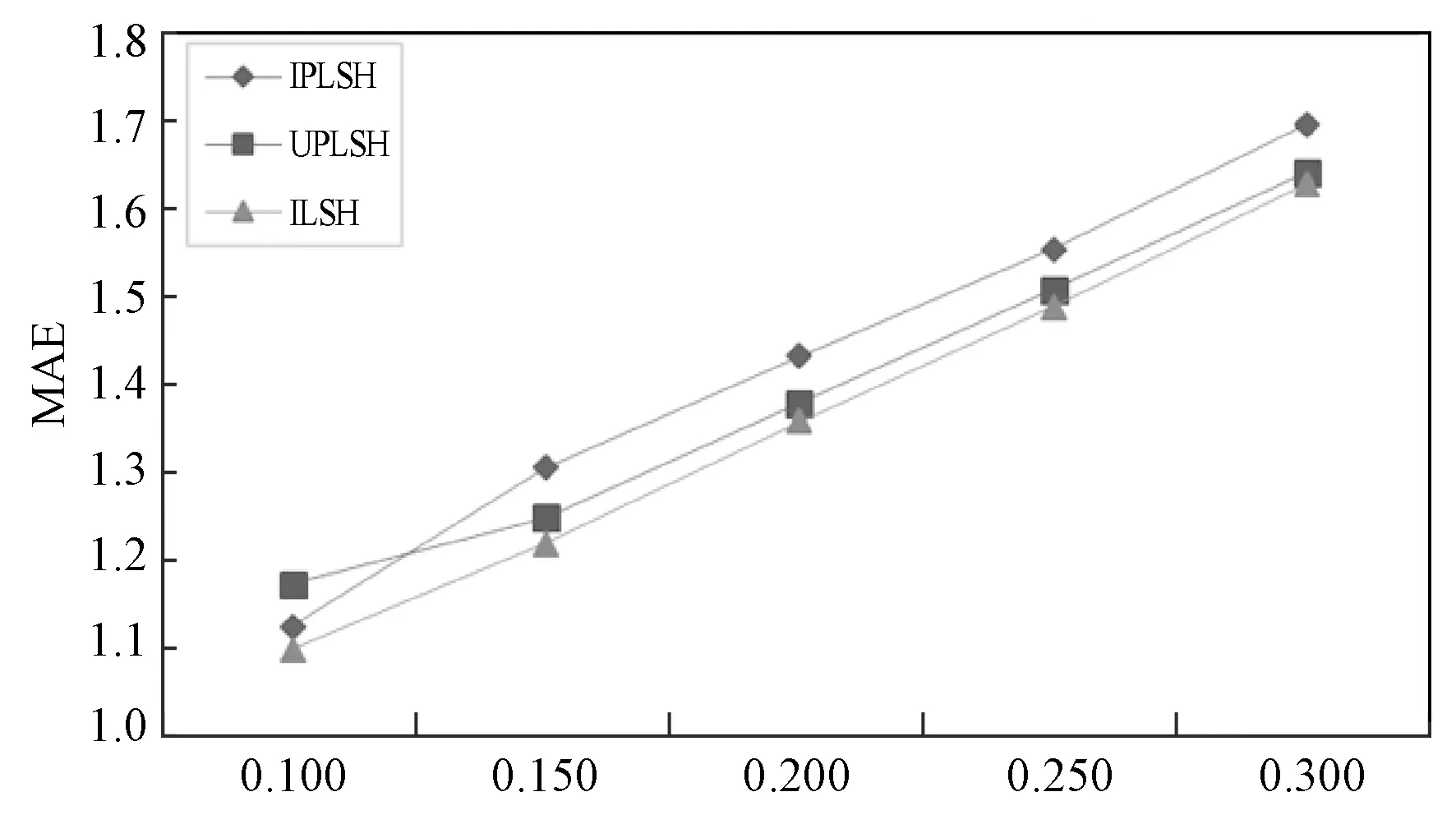
图7 相关LSH算法与ILSH算法的MAE应 对数据稀疏度的变化对比
从图7中可以看出,本文提出的ILSH算法的MAE值一直处于较低的水平且一直比IPLSH和UPLSH要低。这验证了ILSH算法的相对稳定性和准确性。
5 结 语
针对物品推荐体系中高维的用户评分数据以及物品选择和管理的数据稀疏性对推荐决策带来的影响,本文基于最新LSH优化算法提出了基于ILSH的统计预测算法。实验表明,本文提出的ILSH能很好地应对海量高维数据近似计算,有效减少数据稀疏度对统计预测精度的影响。今后将基于兴趣偏好的“近邻的近邻也是我的近邻”这一理论,结合机器学习算法提高用户兴趣统计预测结果的准确性和智能性。
