不可压壁湍流中基本相干结构
2020-03-13袁先旭陈坚强涂国华
杨 强, 袁先旭,2,*, 陈坚强,2, 涂国华
(1. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000;2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000)
0 引 言
壁湍流广泛地存在于自然界中,早在500多年前,意大利画家达芬奇便在他的画作中记录了这一复杂的流动现象。长期以来人们认为壁湍流是杂乱无序的,直到1967年,斯坦福大学Kline等[1]采用氢气泡示踪法证实了壁湍流中存在近似规则的低速条带结构(Streaks),如图1。这些条带结构在往下游演化的过程中会发生摆动,然后急骤破碎,进而伴随大量雷诺应力的产生[2]。Kline等将这一过程命名为“猝发”(Bursting)。
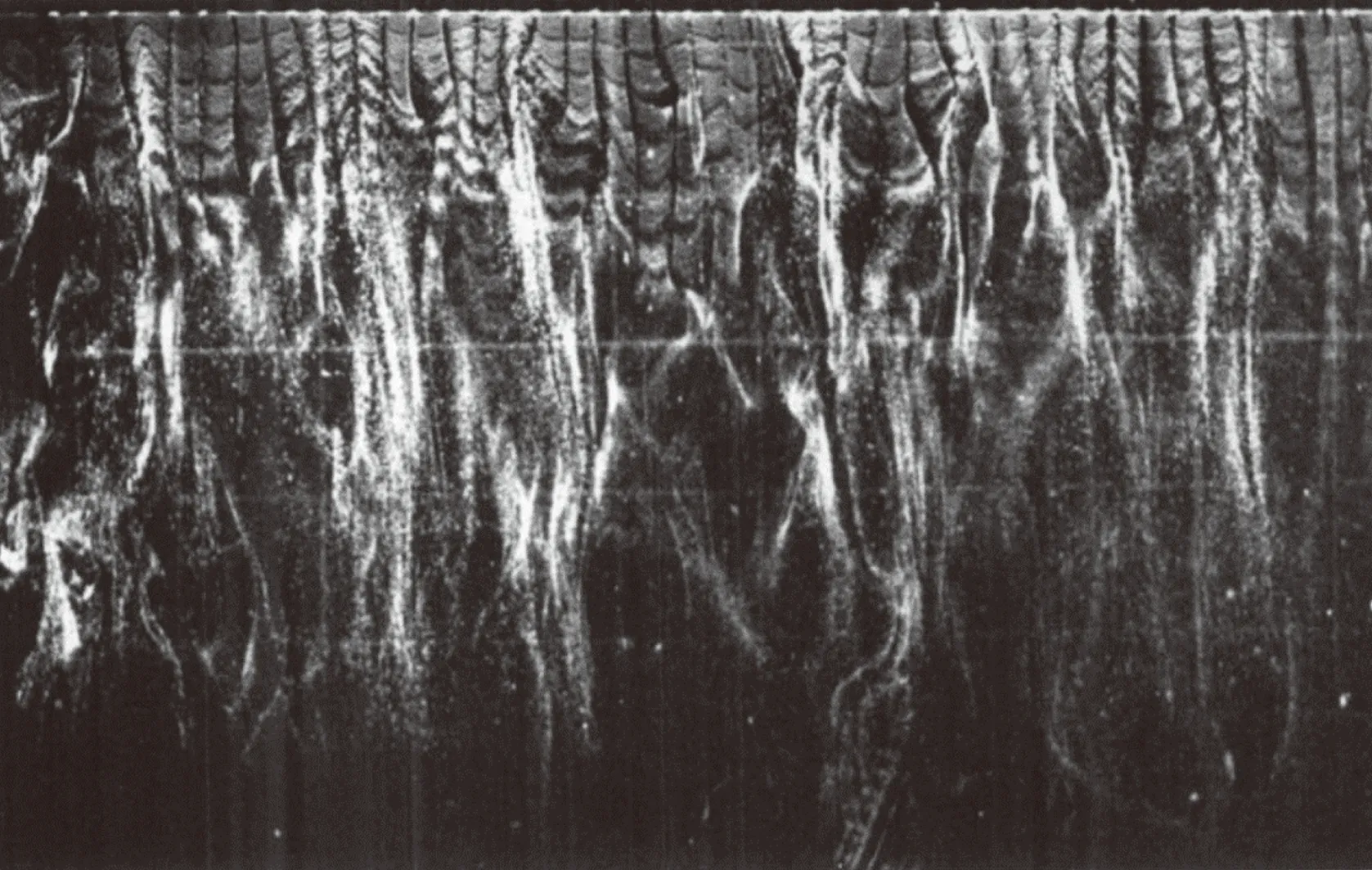
图1 氢气泡示踪的近壁条带结构[1]Fig.1 Hydrogen bubbles visualized near-wall streaks[1]
到1981年,Head和Bandyopadhyay[3]采用烟线示踪方法发现了壁湍流边界层中的流向涡结构。它们依形态分有发卡涡、马蹄涡、Ω涡等,分别对应于湍流演化的不同阶段和不同区域[4]。这其中最常见的就是发卡涡结构(如图2),它由正向和反向旋转的两条涡腿及头部组成,实际壁湍流中以不对称的形态为主,即通常无头部且只出现一条涡腿。同时发卡涡也可以抱团形成更大的涡包[5]。
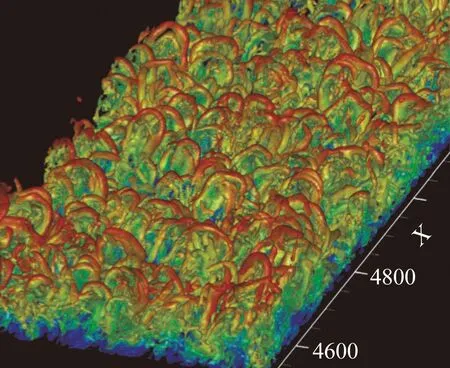
图2 直接数值模拟的发卡涡结构[6]Fig.2 Hairpin vortex structures from DNS[6]
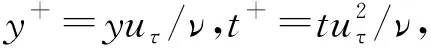
1 湍流结构的自相似
过去一个世纪的壁湍流研究中最大的发现之一是壁定律[7-8],即湍流边界层包含黏性子区(y+<5);缓冲区(5
Townsend[12-13]较早意识到壁湍流的对数律暗示着壁湍流中存在一系列大小与其中心离壁面距离成正比的附面涡结构,并给出了壁湍流中最早的统计模型(双锥模型,如图3)。通过假设湍流边界层中具有一系列不同大小的附面涡且它们具有相似的速度分布,Townsend成功地导出了无穷大雷诺数下流向平均速度的对数律,同时他还预测在无穷大雷诺数下壁湍流的流向和展向速度脉动也存在对数律,而法向速度和雷诺应力为常数。这一预测结果后来得到了实验[14-15]和DNS[16-17]的证实。Townsend的附面涡模型(AEM)后来得到进一步发展[18-20],Marusic & Monty[21]最近对这方面的工作进行了综述。需要指出的是Townsend的附面涡只是统计意义上抽象的湍流相干结构模型,它可以包含实际观察到的条带和流向涡结构。

图3 Townsend提出的壁湍流中的双锥模型[13]Fig.3 Double-cone model for wall-bounded turbulence proposed by Townsend[13]
Townsend的附面涡模型与Richardson[22]的能量级串具有一定的相似性。能量由最大含能涡进入系统,然后经过惯性子区尺度间能量的逐级传递,最终至Kolmogorov尺度完成能量耗散[23]。对于壁湍流,这种能量级串的过程发生在不同的壁面高度。由于壁面的约束,使得不同的壁面高度处的含能尺度和耗散尺度随高度发生变化。Jiménez[24]分析了高雷诺数壁湍流中的湍动能谱和耗散能谱,发现含能尺度和Kolmogorov耗散尺度随着高度增大而增大,而且两个尺度间的分离也随高度增加而增加,表明在更高的壁面位置需要经历更长的能量级串历程(如图4)。大部分能量在其生成高度完成耗散,但由于不同壁面高度处相干结构间的相互作用,能量也沿壁面高度发生传递。Townsend的附面涡模型反映了这一含能尺度的分布规律,同时,由于附面涡尺度随壁面距离发生变化,同一附面涡在较低高度是含能尺度,但在较高高度却可能也是惯性区尺度。

图4 壁湍流中沿壁面高度的能量生成与耗散能谱[24]Fig.4 Energy production and dissipation spectra along wall-normal distance in wall-bounded turbulence[24]
1.1 近壁区
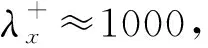

图5 壁湍流中条带和流向涡结构示意图[26]Fig.5 Schematics of streaks and streamwise vortices in wall-bounded turbulence[26]
Willmarth等[30-32]对壁湍流中的雷诺应力-u′v′进行了象限分析,依(u′,v′)的符号将雷诺应力分为Q1、Q2、Q3和Q4事件。旋转的流向涡在一侧将近壁的低速流体带到远壁区,形成上抛(Ejection),对应Q2事件;而在另一侧将远壁面的高速流体带到近壁区,形成下扫(Sweep),对应Q4事件。Q2和Q4事件是壁湍流雷诺应力的主要贡献者,且靠近壁面区(y+<12)由Q4事件主导,而远离壁面区由Q2事件主导[9]。这两个事件直接造成流向速度的法向梯度增加,形成壁面的高摩阻区域[33]。图5给出的条带和流向涡相干结构的分布能够很好地解释壁湍流中包括上抛和下扫在内的诸多实验观测到的现象。
1.2 远壁区
随着实验和计算技术的不断进步,壁湍流研究的雷诺数也在不断提高,如直接数值模拟的最高雷诺数已从Reτ=180上升到Reτ=8000[9,16-17,27,34-36],实验雷诺数目前最高已达到Reτ=O(106)量级[15,37]。从湍流统计量来看,高雷诺数湍流中最直观的反映是:湍流脉动量和能谱分布中除了内区峰值外,在外区也出现了一个新的峰值,且外区峰值能量随雷诺数增加逐渐升高(如图6)[38]。这一现象预示着高雷诺数湍流中外区相干结构的作用不容忽视,因此自上世纪末它们成为壁湍流研究新的热点。
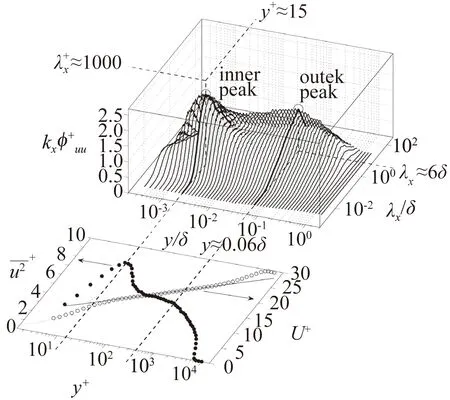
图6 流向速度脉动的一维预乘谱和统计平均量[39]Fig.6 One-dimensional pre-multiplied spectra and statistical mean of streamwise velocity fluctuations[39]
实验中很早就观察到在边界层的外缘存在大尺度的湍流结构,它们将边界层的湍流区和层流区沿法向分开,其大小为O(δ)量级[40]。Meinhart[41]通过PIV测量发现湍流边界层远壁区存在均匀的流向速度动量区,与近壁区的条带结构类似,但流向尺度为2δ~3δ,展向尺度为1δ~1.5δ,这一结构被命名为大尺度结构(LSM)。接着,Kim & Adrian[42]在Reτ=3175圆管流动测量中发现远壁区除了长度为2δ~3δ的大尺度结构外,还存在长度为14δ的超大尺度的湍流结构(VLSM)。Hutchins & Marusic[38]分析Reτ=O(106)大气边界层数据,也发现远壁区存在20δ的超大尺度结构,并将其称为超结构(Superstructures)。dellamo & Jiménez[43]对Reτ=550泊肃叶流动的DNS数据库分析发现其中存在长度大于5δ的超大尺度结构,且在更高雷诺数下变得更为清晰(如图7)[44]。Monty等[45]对平板边界层流动、槽道流动和圆管流动中的大尺度/超大尺度结构进行了综合比较,发现大尺度/超大尺度结构广泛地存在于这些典型流动的对数区和外区(远壁区)。

图7 高雷诺数壁湍流中的超大尺度结构[44]Fig.7 VLSM in high Reynolds number turbulence[44]
远壁区的这些大尺度/超大尺度结构在统计意义上存在自相似性[46-52],与Townsend的附面涡模型描述情形一致。关于远壁区大尺度/超大尺度结构的形成,Adrian 等[53]结合实验观测结果给出了解释:大量的流向涡聚集在一起会形成更大的涡团(如图7),涡团的上抛和下扫形成了大尺度的均匀动量区,而多个均匀的动量区又会进一步聚集形成更长的均匀动量区,即所谓的“Bottom-up”效应。但最新数值实验表明,外区的大尺度结构可以不依赖近壁的小尺度结构而单独存在[54-55],因此“Bottom-up”可能并非远壁区大尺度/超大尺度结构生成的机制,后面将继续论述这一点。
高雷诺数下,远壁区的这些大尺度/超大尺度结构对近壁区的动力学和统计学行为有着重要影响,主要表现为“叠加”(Superposition)和“调制”(Modulation)两种作用[39,56-57],即所谓的“Top-down”效应。由于大尺度/超大尺度结构的存在,近壁区的湍流速度脉动的峰值即便在黏性尺度下也不是固定不变,而是随着雷诺数升高不断增加[58-59]。这些大尺度/超大尺度结构对壁面摩阻有着重要贡献,在Reτ≈2000时贡献率已达20%~30%[60]。远壁区的大尺度结构对近壁区的小尺度结构的幅值、频率、相位、对流速度等均有影响[39,59,61-65],且高速大尺度结构和低速大尺度结构对近壁区小尺度结构产生的影响是不同的[66-68]。据此,Marusic等[69-71]提出了一种近壁流动参数的预测模型,仅通过测量远壁区流动量便可预测出近壁区的流动参数(如图8)。然而,Toh & Itano[72]认为近壁区的小尺度结构与远壁区的大尺度结构间的作用不是单方面的,而是相互依存影响的,即所谓的“Co-supporting”机制。目前,内外区不同尺度间的相互干扰仍是一个尚无共识的领域,有待进一步探索。
高雷诺数壁湍流是一个刚刚兴起的研究热点,里面有许多新的物理现象和开放性问题[73],感兴趣的读者可以参考最近的综述文章[5,24,37,74-76]。
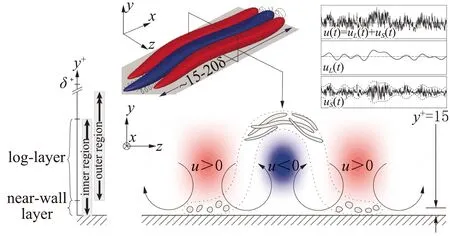
图8 内区和外区湍流结构相互作用[69]Fig.8 Interaction between turbulence structures in the inner and outer regions[69]
2 湍流结构的自维持
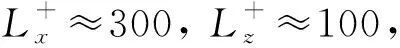
Mizuno & Jiménez[80]研究槽道湍流时人为地将壁面移除,在对数区施加约束条件,发现近壁区的湍流结构消失了,但对数区和外区的湍流结构和统计量几乎没有受到影响。这一结果说明,壁面的存在仅仅是提供湍流生成所需的平均速度剪切,且对数区的相干结构可以不依赖于近壁区相干结构独立存在。Hwang & Cossu[81]对此作了进一步证实。他们在对数区MFU中人为提高大涡模拟的Smagorinsky涡黏系数CS以抹去近壁区的湍流结构,发现对数区的湍流结构仍然能够自维持。Hwang & Cossu[54]在大槽道中采用同样的方法将近壁区和对数区的湍流结构都人为抹去,发现外区的大尺度湍流结构仍能自维持。由此说明壁湍流结构在各个壁面高度都能独立存在——壁湍流的自维持现象。
为了探寻壁湍流自维持的机理,Hamilton等[82]基于库特叶流动的MFU率先对缓冲区进行了研究,提出了壁湍流自维持的闭环(如图9)。这个过程描述如下:1. 由于“Lift-up”效应,流向涡激发出流向均匀的条带结构(线性过程);2. 流向均匀的条带由于瞬态增长或二次失稳变得蜿蜒最终破碎;3. 具有流向梯度的流场在非线性作用下生成流向涡(非线性过程)。湍流的自维持将前面实验和计算中所观察到的条带和流向涡紧紧地联系在了一起,两者互相依存,缺一不可。最近发现,缓冲区的自维持过程同样也适用于对数区和外区湍流相干结构[55,83],破坏三个环节中的任何一环都会造成流动的层流化。图10展示了对数区MFU中的一个典型的自维持过程。最近,Yang等[84]发现自维持过程也可以在Kolmogorov尺度上发生,但是此过程的能量生成量相对于能量级串过程的能量传递量是很小的。

图9 湍流自维持过程的闭环[82]Fig.9 Cycle of the self-sustaining process of turbulence[82]

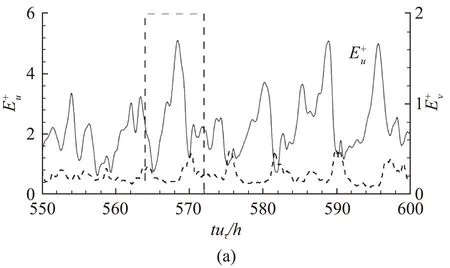
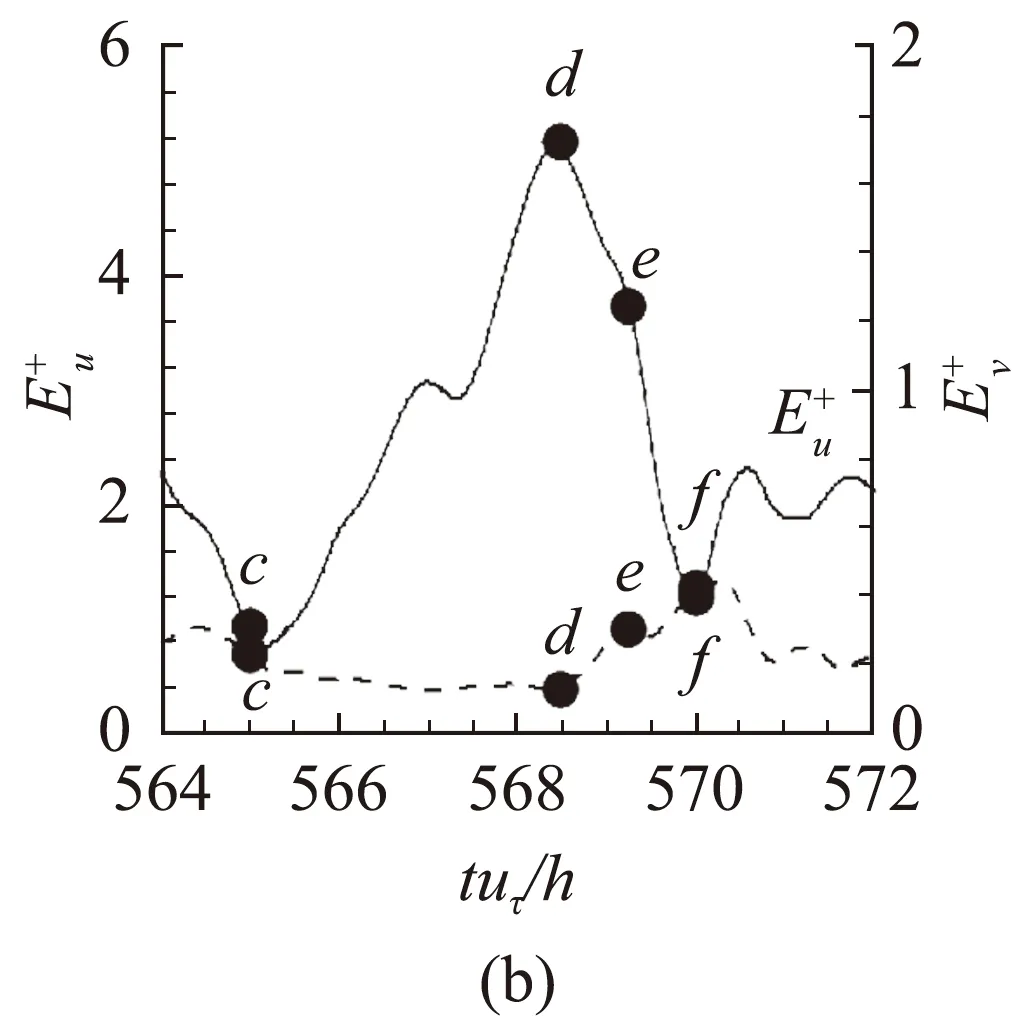
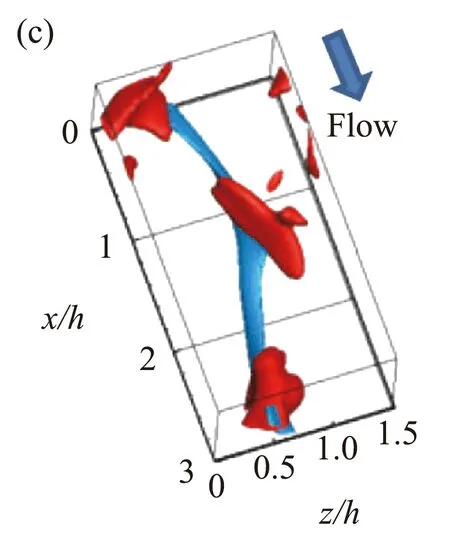
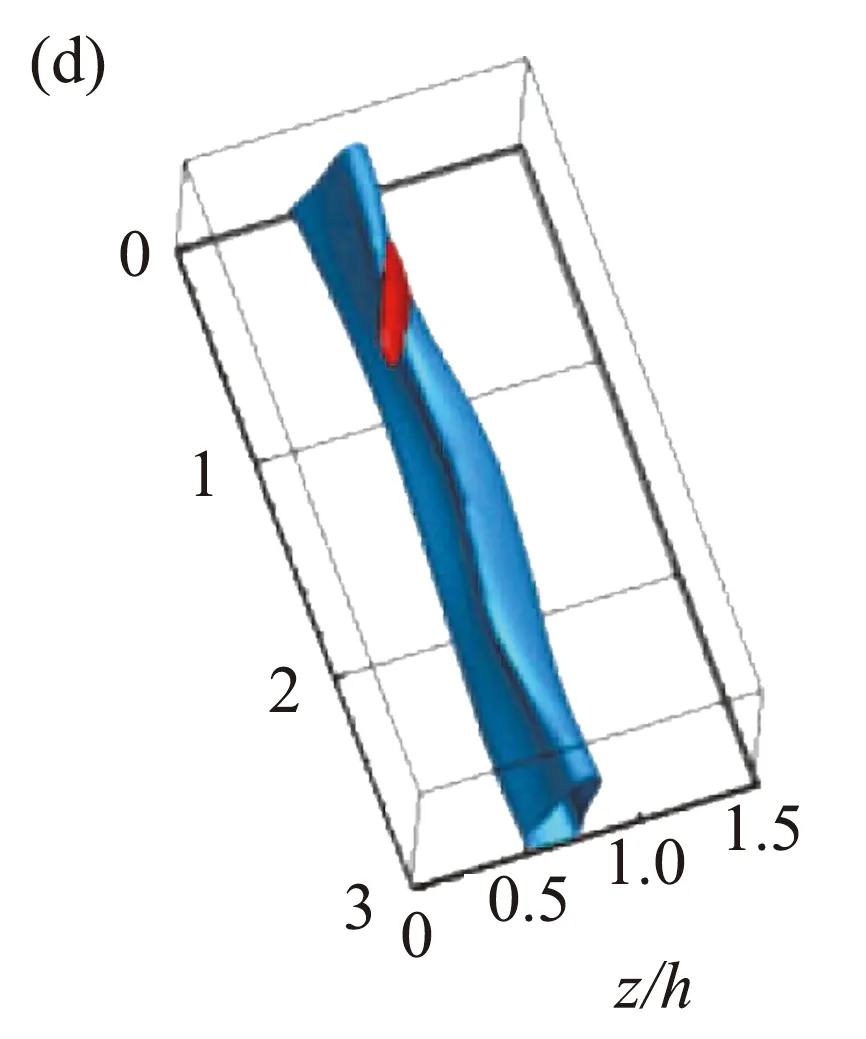
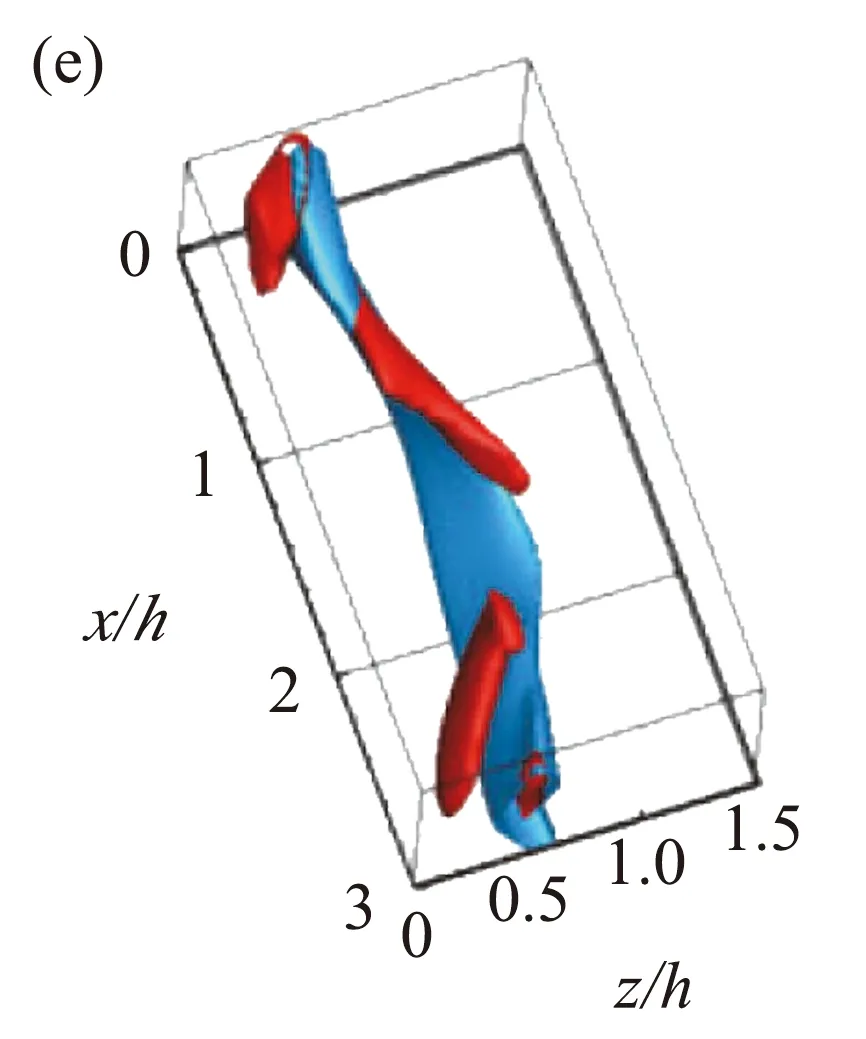

图10 对数区的自维持过程[83]:(a,b)流向和法向速度脉动能量随时间的演化;(c-f)典型时刻的条带和流向涡结构Fig.10 SSP in the logarithmic region[83]: (a,b) time evolution of streamwise and wall-normal velocity fluctuation energy; (c-f) streaks and streamwise vortices at typical instances
基于Townsend的附面涡模型,最近Hwang[50]提出了一个适用于内区、对数区和外区的湍流相干结构的统一框架:在给定壁面高度y,存在尺度为λx≈10λz,λz≈10y的条带(流向速度脉动量)和尺度为λx≈2~3λz,λz≈1~2y的流向涡结构(法向和展向速度脉动量);对于近壁区,y=10ν/uτ;对于外区,y=δ。每个壁面高度的条带和流向涡形成自维持的闭环。实验和计算中观察到的LSM和VLSM可以分别看作是外区的流向涡和条带结构。
2.1 条带的生成
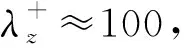
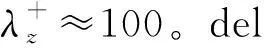

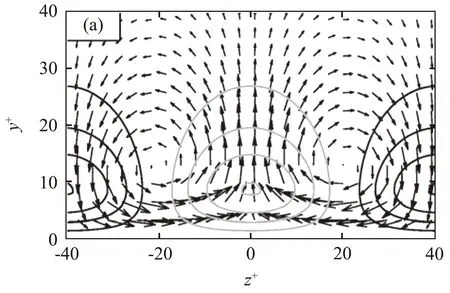
(a) 内区

(b) 外区[101]
2.2 流向涡的生成
流向涡的生成主要有两类解释[105]:一种是“Parent-offspring”机制;另一种是条带不稳定性(“Streak-instability”)机制。“Parent-offspring”机制更具有唯象性,需要预先有流向涡存在;而条带不稳定性机制是基于稳定性理论,不需要预先有流向涡存在,但需要有条带存在。
Brooke & Hanratty[106]通过观察展向和法向二维涡截面,发现流场中的流向涡通过下扫在壁面生成流向涡量进而演化成新的流向涡,类似于偶极子涡在壁面的反弹过程[107]。然而现在的研究更多地发现壁面的存在并不是壁湍流自维持所必需的[80],说明基于壁面的涡生成机制不是主要的。Zhou等[108]通过直接数值模拟观测到当流向涡超过一定的强度后,会在边部生成新的二次流向涡,然后二次流向涡又会生成新的三次流向涡。
从湍流自维持的角度,条带不稳定性机制更被接受。饱和的条带具有不同的失稳模态:反对称模态的失稳对应着交错排列的流向涡结构;对称模态的失稳对应着发夹涡结构,其中反对称模态失稳更为常见[109-110],也更为危险[111]。Schoppa & Hussain[112]详细讨论了基于当地稳定性理论的饱和条带失稳形成流向涡的过程。Schoppa & Hussain[86]发现湍流中实际满足失稳条件的条带所占比例很小,大部分条带是通过瞬态增长途径实现失稳的,称为条带的瞬态增长(STG)机制。图12展示了通过STG生成的流向交错排列的流向涡,与DNS结果十分类似(见图5)。

图12 STG生成的流向涡[86]Fig.12 STG generated streamwise vortices[86]
3 精确相干态
意识到湍流中的自维持后,Waleffe[110,113]尝试获得一个简化的数学模型来描述这一过程。他将滑移壁面条件下的N-S方程分解成流向速度部分(条带)和法向、展向速度部分(流向涡)。由于流向均匀的条带无法失稳形成流向涡,因此引入一个人为的体积力以维持流向涡。然后,Waleffe[113]逐渐降低体积力的大小至零,发现由于非线性的作用系统中出现了两个自维持的状态。Waleffe[114]进一步将这两个自维持态延拓到无滑移壁面条件下,获得了泊肃叶流动中的首个N-S方程的非线性解(又称不变解,见图13)。这一非线性解具有蜿蜒的流向条带和伴随两侧的流向涡结构,以一固定的相速度向下游传播(行波解),在相对坐标系下解的结构不发生变化,与Jeong等[26]从DNS湍流场提取的湍流相干结构(见图5)极为相似,因此这个非线性解被普遍认为是对湍流的自维持过程的精确描述[75]。鉴于此,Waleffe率先将这个非线性解命名为精确相干态(ECS,又称精确相干结构)[114]。从动力系统的角度看,ECS的种类有很多,包括湍流的平衡态、行波解、周期轨道及其包络等,湍流即是在这些ECS间穿梭[115-116]。Jiménez等[87]将ECS和MFU及全尺度湍流近壁区的统计量和猝发特征进行了比较,发现ECS可以作为一个简化的系统进行湍流研究。

图13 泊肃叶流动中的ECS[114]Fig.13 ECS in Poiseuille flow[114]
将ECS沿雷诺数进行延拓就可以获得一条分叉曲线,转折点为鞍-结点,是下支的鞍点与上支的结点汇聚的地方。在给定雷诺数下,上支ECS摩阻比下支ECS高很多,流向涡强度更大、条带更蜿蜒[114]。从动力系统角度看上支ECS是湍流区的平衡态/准平衡态,湍流运动轨迹在它附近停留一段时间后再沿其不稳定包络转移到另一个平衡态/准平衡态。下支ECS位于湍流与层流的分界面(Edge of Chaos),至少有一个不稳定的特征方向,从一侧施加扰动可以快速地到达湍流区,而从另一侧施加扰动可以快速地到达层流态(如图14)。如果下支ECS有且只有一个不稳定的特征方向,它也被称为边界态(Edge State)[117]。可见,ECS不仅是充分发展湍流里的基本相干结构,它也是转捩过程中的基本相干结构。需要指出的是,真正意义上的首个ECS是Nagata[118]分析库特叶流动的亚临界失稳时通过对泰勒-库特叶流动进行同伦变换获得的,随后Clever & Busse[119]在研究热对流问题时也通过同伦变换获得了相同的解,它与Waleffe[114]从自维持角度发现的泊肃叶流动中的ECS是同一族解,统称为NBCW解。同样采用人为体积力的方法[113],Faisst & Eckhardt[120]和Wedin & Kerswell[121]获得了圆管流动中的NBCW解。这样,ECS就将各种剪切流动中的充分发展湍流与转捩过程统一在了同一分析框架中。由于ECS通常是不稳定的,实际流动中很难观测到,但最终Hof等[122]通过精细的实验首次在圆管中拍到了ECS,证实了精确相干态的真实性。
ECS是从湍流自维持的角度考虑N-S方程的非线性解,而实际中这样含有流向涡与条带的三维相干结构在其它的理论中也有发现。比如,Hall & Smith[124]研究无穷大雷诺数下T-S波与流向涡的非线性作用时,发展了一套涡波干扰(VWI)理论。通过VWI理论获得的解其实是ECS在无穷大雷诺数下的渐近态[125]。McKeon & Sharma[126]将N-S方程的非线性作用视为一个随机力效应,发展了湍流的Resolvent分析方法,可以较好地反映壁湍动中一系列的相干结构[76]。最近,他们发现只需要几个Resolvent模态就可以构造出ECS[127-128]。
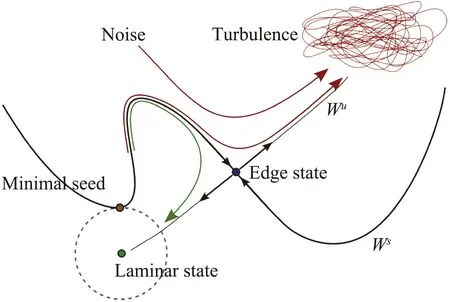
图14 态空间内的边界态示意图[123]Fig.14 Schematics of the edge state in the state space[123]
3.1 全湍流区
Kawahara & Kida[129]获得了库特叶流动中的首个周期轨道,完整地再现了湍流自维持中条带的生成破碎和流向涡的生长衰减过程(如图15)。从相空间看,湍流在这个周期轨道上停留了大量的时间,因此仅此单个轨道周期内的统计量(平均速度和速度脉动均分根)就与湍流统计量十分吻合。Jiménez & Simens[130]在MFU中通过衰减函数移除外区某一高度Δ+以上的湍流结构后获得了近壁区的低维度相干结构,与ECS十分相似:当Δ+>50时,此相干结构为一行波解;当Δ+>60,此相干结构为含有两个频率的周期轨道。Toh & Itano[131]采用打靶法发现了泊肃叶流动中的一个周期轨道。这个周期轨道是一个边界态,由两个典型的状态构成:一个状态只含有一个条带;另一个状态含有两个条带,两个状态的转换对应了猝发过程。Kreilos等[132]在渐近吸气边界层中也发现了类似的非定常边界态,并作了更细致的研究。低雷诺数壁湍流中像这样的ECS已有大量报道[133-135]。
由于外区的湍流结构存在自维持[54],Hwang等[136]尝试寻找外区的ECS。他们在Reτ≈1000泊肃叶流动中采用过度提高Smagorinsky涡黏系数CS的方法分离出外区的大尺度结构,并以此作为二分法的初始流场,进而获得了外区湍流的ECS。同样地,上支解相比于下支解对应的条带更蜿蜒,且流向涡强度更高(图16)。

图15 库特叶流动中的周期轨道[129]Fig.15 The periodic orbit in Couette flow[129]
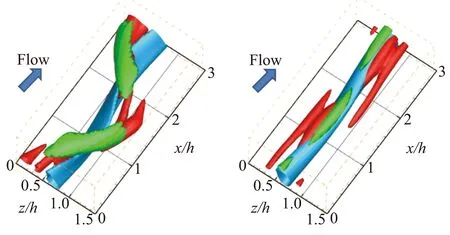
(a) 上支 (b)下支
图16 外区的ECS[136]
Fig.16 ECS in the outer region[136]
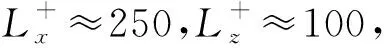
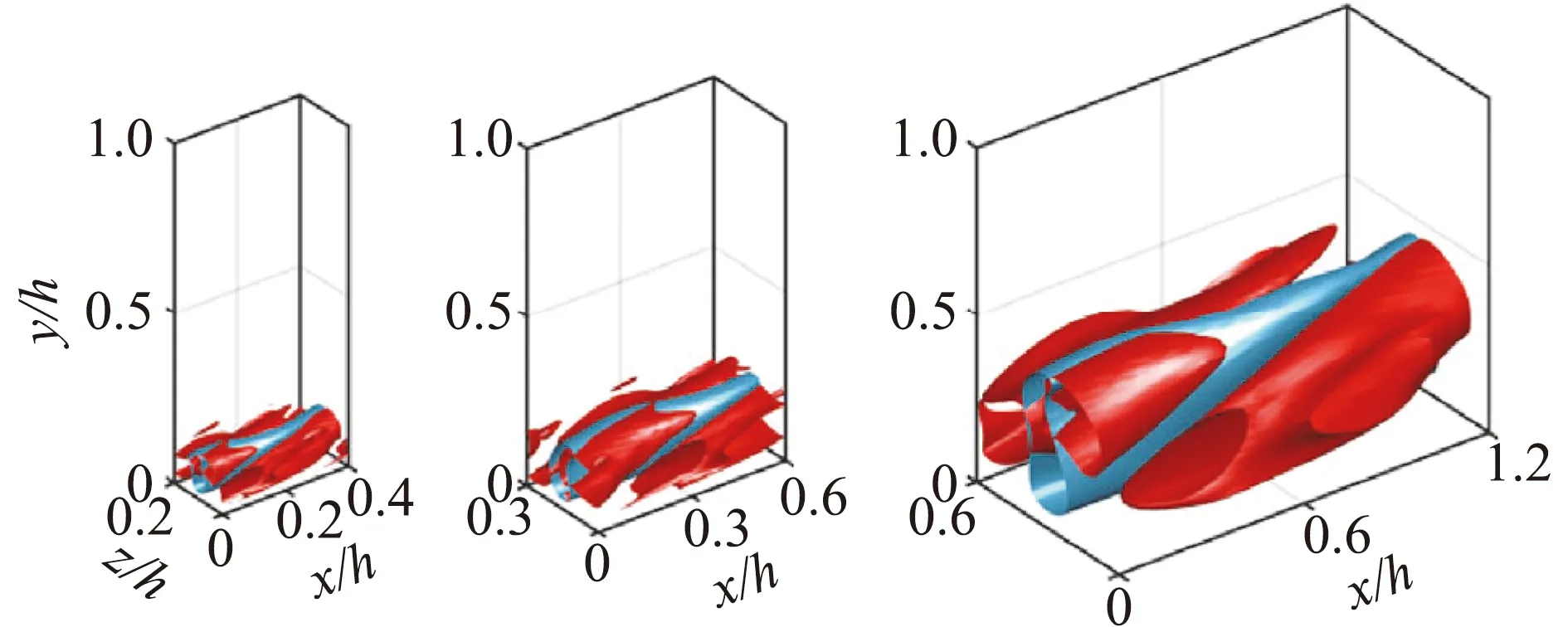
图17 法向局域化的ECS[137]Fig.17 Wall-normal localized ECS[137]
ECS可以具有不同的对称性。NBCW解满足平移-翻转对称性,对应于条带的反对称不稳定模态,因而获得的ECS含有沿流向交错排列的流向涡结构。Gibson等[135]通过在泊肃叶流动中引入不同的对称性,获得了一系列新的ECS。Itano & Generalis[145]和Deguchi & Nagata[146]获得了库特叶流动中具有展向镜像对称性的ECS,与发卡涡类似。Nagata & Deguchi[147]和Shekar & Graham[148]在泊肃叶流动中引入了展向镜像对称,也获得了发卡涡形式的ECS。图18展示了发卡涡形式的ECS[149]。

图18 发卡涡形式的ECS[149]Fig.18 Hairpin-like ECS[149]
当然,N-S方程描述的是一个高维的动力系统,其中存在的ECS非常多,所幸的是典型ECS的不稳定包络的个数并不太多,如果能够找到所有的这些典型的ECS构成的湍流的骨架,那么湍流的动力学行为就能很好地得以描述了[115]。Kawahara等[150]对湍流中ECS的重要性作了全面的综述。
3.2 转捩区
从ECS的角度看,转捩区湍流与充分发展湍流是相关联的,二者统一于非线性的N-S方程,这区别于传统的基于线化N-S方程的转捩研究。对于典型的壁湍流,库特叶流动和圆管流动是线性稳定的[151-152],泊肃叶流动的临界雷诺数是Rec=5772[153-154]。然而,通常实验中在Re≈1000就会发生转捩[155]。不可压边界层流动的临界雷诺数为Rec=520[156-157],当来流噪声较高时实验中也能观察到较低雷诺数的转捩。由于这些典型流动的转捩雷诺数要低于线性稳定性预测的失稳雷诺数,因此称为亚临界转捩;另外,由于这种转捩过程没有二维T-S波的增长过程,而是直接出现沿展向变化的条带结构,因此也称为Bypass转捩[158]。这种转捩途径给传统的基于小扰动的线性稳定性分析带来了挑战[159]。
从动力系统的角度看,流动可以看作由层流态经过一系列的Hopf分叉形成新的平衡态/准平衡态直至成为湍流,这也是早期Landau的观点[160]。然而,研究发现亚临界转捩并不是源自层流态连续的Hopf分叉,而是源于前面叙述的NBCW解的鞍-结点分叉[161-162]。图19显示了库特叶流动经过一系列的分叉(包括鞍-结点分叉、Hopf分叉、倍周期分叉和危机分叉)从NBCW解发展为湍流的过程。对于泊肃叶流动,存在二次平衡态[163-165],其失稳雷诺数为Rec=2900[166-167]。Ehrenstein & Koch[168]基于此二次平衡态失稳获得了三次平衡态,进而得到了更低的临界雷诺数Rec≈1000,然而,这个三次平衡态的存在有可能是由于他们计算中过度的截断误差引起的虚假解[147]。进一步地,对于线性稳定的库特叶流动和圆管流动,流动无法通过首次失稳获得二次平衡态。为此,Cherhabili & Ehrenstein[169]将泊肃叶流动中的二次平衡态延拓到库特叶流动中,发现其为展向均匀而流向局域化的孤立波形态;并基于此二次平衡态的失稳获得了三次平衡态,同样具有流向局域化特征,是不同于NBCW解的一族新的解。因此,从目前的认识来看,对于亚临界转捩,相对于层流态的直接失稳,湍流态更易源自鞍-结点分叉形成的ECS,也即Nagata所谓的无穷远处的分叉。考虑鞍-结点分叉后,对于泊肃叶流动、库特叶流动和圆管流动,其临界雷诺数分别降低到Rec=977[170],Rec=125[104,118],Rec=1250[120],均与实验观测到的临界雷诺数比较接近。

图19 库特叶流动中的亚临界转捩过程[171]Fig.19 Subcritical transition process in Couette flow[171]
鞍-结点分叉曲线下支的ECS(尤其是边界态)与亚临界转捩最为相关,其条带和流向涡的幅值与雷诺数分别满足Re0和Re-1的标度率[125,172-173],因此在高雷诺数下,来流中只需要很小的扰动就可以激发出自维持的ECS,进而使流动沿着ECS的不稳定包络进入湍流。由此生成的湍流的生命周期随雷诺数呈指数增长[174-176]。由于ECS广泛地存在于各种剪切流动中[141-144,177],这种转捩途径具有普适性,据此Cherubini等[178]提出了一条完全非线性的转捩途径(图20)。实际流动中,非线性最优扰动是触发湍流的最小能量种子(Minimum Seeds)[103,179-185],它也是由条带和流向涡构成,与边界态非常接近。从动力系统的角度看触发湍流的最小能量种子实际上是位于湍流与层流的边界靠近湍流态的一侧,在相空间里距离湍流态最近(图20);相对而言,线性最优扰动位于湍流与层流的边界靠近层流态一侧,因此其对湍流的激发效率要低于最小能量种子[103]。
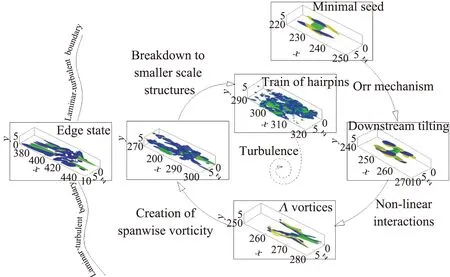
图20 边界层内的非线性转捩路径[178]Fig.20 A nonlinear transition path in boundary layer flow[178]
与最小能量种子形态一致,实际亚临界转捩过程中出现的扰动形态通常是局域化的,如湍斑[186-188]、湍带[189-192]等,它们将流动分成湍流与层流相间的状态。与之对应的是位于层流/湍流边界上的局域化的、不依赖于计算域大小的边界态,如泊肃叶流动[193-195]、库特叶流动[196-200],圆管流动[201-204]、边界层流动[123,205-206]、渐近吸气边界层流动[207-208]等。图21展示了圆管流动中一个典型的局域化的边界态(又称Puff)。对这些局域化的边界态的分析有助于深入理解转捩的动力学行为:比如,Reetz等[200]发现库特叶流动中倾斜的湍带其实是源自于NBCW解。圆管流动中的亚临界转捩过程也由于Puff的发现变得更为明晰:在低雷诺数下Puff是不随时间发展的平衡态,但随着雷诺数的升高,Puff在流向开始扩展,最终充斥整个圆管形成充分发展湍流[209-213]。
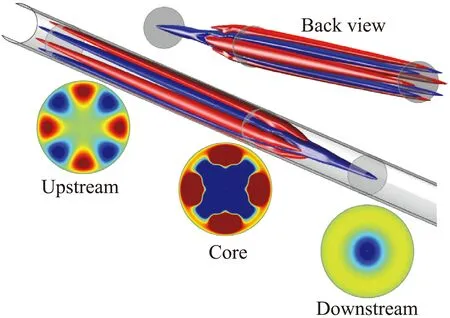
图21 圆管流动中局域化的ECS[201]Fig.21 Localized ECS in pipe flow[201]
4 总结与展望
壁湍流是一个复杂的多尺度系统,湍流相干结构的发现及研究极大地提升了我们对壁湍流的认识。经过一个多世纪的研究,近壁区的湍流行为被认识得已较为透彻。当前,高雷诺数壁湍流成为新的研究热点,一些新的流动现象,尤其是壁湍流中含能尺度的多样性问题更为凸显。基于目前对壁湍流相干结构的认识,其最核心的特征是不同壁面高度相干结构的自相似和给定壁面高度下相干结构的自维持。为此,关于近壁区湍流相干结构的一些性质、规律可以为对数区和外区的湍流相干结构的研究提供很好的借鉴。从湍流相干结构出发,Townsend的附面涡模型已经在壁湍流的数值模拟方面展现出了一定的生机。但与此同时,我们也应该看到,尺度分离/尺度干扰将是不可压高雷诺数壁湍流研究中不可规避的重要问题。
长期以来,湍流与转捩作为流体力学两个独立的分支分别开展着各自的研究,ECS的发现让非线性动力系统理论架起了统一研究二者的桥梁。亚临界转捩(乃至一般转捩的后期)湍斑/湍带中的相干结构与充分发展湍流中的相干结构是十分类似的,它们所对应的ECS也是一致的,均是由条带和流向涡构成的自维持单元。认识这些基本的ECS的性质有望后续精确地进行转捩路径和湍流运动轨迹的预测。Barkley[213]已经对圆管流动的亚临界转捩展开了卓有成效地模型预测。目前也有学者开始针对ECS开展湍流/转捩相关的控制研究,并获得了一定的效果[214-216]。但是我们也必须认识到湍流的高维特性,从动力系统角度实现湍流的预测仍然需要大量的工作。
最后,壁湍流相干结构的认识目前主要集中在不可压流动中,而可压流动中涉及到马赫数效应、温度效应等,其相干结构尤其是ECS可能出现不同于不可压情形的动力学行为,值得未来研究。
