点·线·网式分析攻克应用问题
2020-03-12王芳
王芳


【摘要】数学知识的学习方方面面都渗透着应用题教学,解决应用问题是考查学生能否运用所学数学知识解决实际问题的基本内容和重要途径.部分学生和教师在应用题的学习和教学中都存在着困惑,本文以北师大版七年级教材部分习题为例,阐述了初中数学应用题教学的六点实践策略,结合设计的应用题分析细项表格,引领学生以以点连线、以线结网的方式对典型例题进行点·线·网式分析,渗透着学生文字语言、图形语言、符号语言的相互转换能力,提升学生的数学建模能力.教师引导学生开展一连串环环相扣、由浅入深的探索,学习数学思维的方式方法,发展数学能力,才是学习数学的根本所在.
【关键词】等量关系;策略;点·线·网式分析
杜威指出:“学习就是要学会思维”“教育在理智方面的任务是形成清醒的、细心的、透彻的思维习惯”.[1]郅庭瑾也指出:“只有学会思维,学会创造性的思维才是最核心和最首要的”.[2]应用题学习贯穿于学生中小学阶段的各个知识板块,有效考查了学生的数学综合素养,但往往在此部分的学习中,学生总有雾里看花之感,本文记录了笔者在教学实践中对应用题教学的思考与感悟,与同仁分享,以期抛砖引玉.
一、初中数学应用题教学的意义
著名的荷兰数学教育家佛赖登塔尔说过:“与其说学习数学,倒不如说‘数学化”.数学知识的学习方方面面都渗透着应用题教学,解决应用问题是考查学生能否运用所学数学知识解决实际问题的基本内容和重要途径,学生需将多个数学知识点和一些简单的科技知识联系起来,将众多实际问题“数学化”.而“方程”就是刻画现实世界数量关系的一种重要的数学模型,亦是初中“数与代数”领域的核心内容之一.学生解决应用问题的过程,其实就是一个简单的数学建模的过程,通过解决数学应用问题,学生可以综合应用所学的数学知识,从而帮助他们发展抽象、概括等基本数学能力,积累提取信息、建立模型、验证结果等基本数学活动经验,进一步感受数学在生产、生活中的作用和价值.
二、初中数学应用题教学实践中存在的问题
从学生方面来说,存在的问题主要是学生综合运用知识的能力欠缺,这里不仅包括数学知识本身,还包括语文等其他学科的知识.语文知识不足,导致学生不能正确理解应用问题的文本所含的语义,从而不能够提取出有价值的数学信息进行整合;数学知识不够,导致他们不能够用数学的符号语言来概括、表达题目中的数学关系;生活常识、其他学科知识薄弱,导致他们不能够充分理解题目背景中所含有的意味,从而造成信息的缺失.从教师方面来说,存在的主要问题是教师对应用题的教学方法研究不充分,在对应用题进行分析时,对其中的思想方法研究不透彻,不能进行思想方法的归纳、总结与提升,经常就题论题,从而导致学生上课能听懂,下课不会做,更使个别学生放弃对应用题的学习.
三、初中数学应用题教学的实践策略
七年级是整个中学学习的起始,一元一次方程是七年级数学中非常重要的内容,一元一次方程的学习是后续所有方程及函数部分学习的基础,始终以转化思想作为主线贯穿其中,学习中体会数学建模的意义与方法是教师带领学生开启实践应用之门的金钥匙.以下以北师大版七年级数学上册第五章“一元一次方程”相关例题、习题为例,探讨如何帮助学生正确理解题意,理清多种数量间的关联,在繁杂的语言叙述中找到等量关系,从而利用方程解决问题.
对每个实际问题的分析,我们都可用以点连线,以线结网的方式,引导学生理解题意,选择科学合理的方式、方法,将问题“数学化”,具体操作可以从以下几方面开展:
1.牢记所学的周长、面积、体積等公式,利用公式找等量关系.
例1 墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:厘米).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各是多少厘米?(北师大版《七年级数学(上)》142页练习)
在彩绳由梯形变为长方形的过程中,虽然形状变了,但周长不变,可得等量关系:梯形周长=长方形周长,从而利用周长公式,列方程解决问题.
2.熟悉常见的数量关系,根据数量间的关系寻找等量关系.
如距离问题(包含相遇问题或追及问题)、工程问题、利润问题、配料问题、增长率问题、航行问题等,学生首先要看清题目属于哪类问题,头脑中应形成解答此类问题所需要的内容条件,相关数量间的数学关系,带着必要的知识储备解答问题.在同一题目中的几个等量关系中,深入分析未知量之间的内在关联,选择某些等量关系,用含一个未知量的代数式表示其他未知量,找准一个等量关系用以列方程.当然这就需要教师在教学这些问题时,要引导学生对问题中包含的重要的等量关系进行概括、梳理、总结,以成为后续学习的知识基础.
例2 一家商店将某种服装按成本价提高40%后标价,又以八折优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?(北师大版《七年级数学(上)》145页例题)
引导学生做如下分析:本题中出现成本价、标价、实际售价、利润多个量,而这几个量之间有什么关联呢?成本价×(1+40%)=标价 ①,标价×80%=实际售价 ②,实际售价-成本价=利润15元 ③,引导学生找到这三个关系后,发现关系①②中都含有多个未知量,但它们最终都指向了成本价这一未知量,实际售价=(1+40%)×成本价×80%,而将其代入关系③中,发现(1+40%)×成本价×80%-成本价=15,而这恰是含有同一个未知量和已知量的等式,它必是列方程的基本关系,所以可以设成本价为x元,用等量关系①②表示其他的未知量,用等量关系③列方程、求解.
3.辨析题中的关键字词,依照关键字词的提示寻找等量关系.
问题中反映数量间的和差关系、倍数关系,叙述中常有如下的提示:“一共有……”“……比……多(少)……”“……是……的几倍(几分之几)”“……比……的几倍多(或少)……”.我们可以由这些关键字词找等量关系,由等量关系间的内在联系设置合理的未知数,列方程.
例3 某文艺团体为“希望工程”募捐组织了一场义演,成人票8元,学生票5元,共售出1 000张票,筹得票款6 950元,成人票与学生票各售出多少张?(北师大版《七年级数学(上)》147页例题)
学生发现“共售出1 000张票,筹得票款6 950元”是关键语句,教师应通过以下问题来引导学生进行思考:“共”说明1 000张票包括哪几种不同的票?“票款6 950元”又是哪几种票款的和?归纳如下等量关系:成人票数+学生票数=1 000张 ①,成人票款+学生票款=6 950元 ②,8×成人票数=成人票款 ③,5×学生票数=学生票款 ④.根据上述4个等量关系,引导学生讨论如何设未知数,利用哪几个等量关系,表示其余的未知量,找准一个等量关系列方程,学生通过思考,可以得到以下三种不同解法.
解法一:设售出x张学生票,则有
5x+8(1 000-x)=6 950;
解法二:设所得学生票款y元,则有
y5+6 950-y8=1 000;
解法三:设售出学生票a张,成人票b张,则a+b=1 000,5a+8b=6 950.
学生在交流各自设未知数解决问题的不同方法时,发现设未知数的方法不同,方程的复杂程度也不同,因此,在设未知数时要有所选择.通过这样的活动引导,学生进一步积累了解决应用题的活动经验.
4.挖掘题目中隐含的信息,根据隐含条件找等量关系.
引导学生对题目中出现的已知量、未知量开展关联研究,通过读题、析题,让学生明白与找到的数量相关联的未知量有哪些,而这些隐含在题目中的数量间存在的等量关系是解决问题的关键所在.
例4 小刚和小强骑自行车去郊外游玩,事先决定早晨8:00从家里出发,预计每小时骑7.5千米,上午10:00可到达目的地.出发前他们又决定上午9:00到达目的地,那么每小时要骑行多少千米?(北师大版《七年级数学(上)》153页习题)
分析 若8:00出发,10:00到达,则用时2小时,又知原计划每小时骑7.5千米,可得路程为(10-8)×7.5千米,实际9:00到达,则用时1小时.在这一过程中虽然用时缩短,速度加快,但不变的量是距离,这里隐含了距离不变这一重要的条件,因此,利用原计划用时×原计划速度=实际用时×实际速度,列方程解决问题.
5.借助线段图,帮助分析等量关系.
在解方程中也有数形结合的思想,对行程问题,仅从字面意思理解,学生会感到较为抽象,教师教会学生画线段图进行分析,就容易很多.
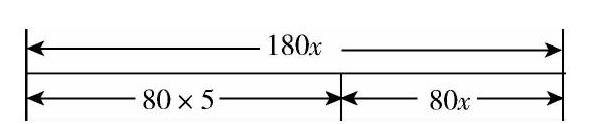
例5 小明每天早上要在7:50之前赶到距家1 000米的学校上学.一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他.爸爸追上小明用了多长时间?(北师大版《七年级数学(上)》150页例题)
在教学中,教师应先画出以下线段图,通过图形,学生能够清楚、直观地发现,此问题中爸爸追上小明时他们所走路程相等,小明5分钟后所用的时间与爸爸追赶他所用时间相同,问题迎刃而解.设爸爸追上小明用了x分,利用以上关系,可知小明所用时间,再利用行程相等建立方程,问题得解.
6.应用题中数量关系较多,相互间关系复杂时,可以利用列表格的方法分析各个量之间的相互关系.
合理的表格可以清晰地整理出多个数量间的逻辑关联,应用题教学中,教师要善于利用表格进行分析,教师应引导学生学习设计表格,尝试让学生自己列表分析,发展学生将实际问题中有关的特征信息进行筛选、加工为数学语言的能力.
例6 星星果汁店中的A种果汁比B种果汁每杯贵1元,小彬和同学买了3杯B种果汁,2杯A种果汁,共花了16元.A种果汁、B种果汁每杯分别是多少元?(北师大版《七年级数学(上)》149页习题)
题目中涉及多种数量,A种果汁的单价和杯数,B种果汁的单价和杯数,A种果汁比B种果汁每杯贵1元,共花了16元.可尝试列表如下:
教师接着提问:A种果汁、B种果汁的单价间有什么关系?如何设未知数?有了表格作为有力帮手,学生很快分析出等量关系,列出方程2(x+1)+3x=16.
在上述六种策略中,寻找资料信息中的关键字词,分析出的已知量、未知量是各个“点”,这些“点”由各类公式、数量关系式或隐含信息串成不同的“线”,“线”与“线”在数学思想方法的逻辑演绎下并成“网”.笔者设计了应用题分析细项表格,将各种解决问题的策略让学生理解透彻,在实践中体会数学化的过程.引领学生以以点连线、以线结网的方式对典型例题进行点·线·网式分析,渗透着学生文字语言、图形语言、符号语言的相互转换能力,提升学生的数学建模能力.
以下展示学生填写完整的表格,供参考.
问题类型追及、相遇问题
题目七年级一班列队以每小时6千米的速度去甲地.小明从队尾以每小时10千米的速度赶到队伍的排头后又以同样的速度返回队尾,一共用了7.5分钟,求队伍的长.
基于理解上的行动,才是最有效的学习行为.教师对现实材料的理解、钻研与再创造,结合所教班级学生的实际学情,选择贴切的教学方法和教学流程,才会使学生真正理解数学知识,感悟数学的理性精神,让学生在具体活动中学会检索、抽取数学信息,利用数学符号进行表达,形成抽象化、形式化的经验,甄别不同数学模型,调整、加工、完善数学模型,由此对所得结果进行解释和说明[3].教师引导学生开展一连串环环相扣、由浅入深的探索,学习数学思维的方式方法,发展数学能力,才是学习数学的根本所在.
【参考文献】
[1]约翰·杜威.我们怎样思維·经验与教育[M].姜文闵,译.北京:人民教育出版社,2005
[2]郅庭瑾.教会学生思维[M].北京:教育科学出版社,2001
[3]董林伟.从理解到行动:数学“四基”教学的若干思考[J].中学教学教学参考,2013(9),8-11.
