引入电压变速因子的反时限零序电流保护方案
2020-03-12李欧
李欧
(广东电网有限责任公司东莞供电局,广东 东莞 523000)
定时限零序电流保护能对各种不对称接地故障作出有效反应,具有整定原则简单、灵敏度高等特点,在电网中得到了广泛应用;但其保护范围受系统运行方式影响,动作时间固定,灵活性差,因而限制了定时限零序电流保护的进一步发展[1-11]。随着电网结构日趋复杂,定时限零序电流保护的整定配合愈发困难。反时限零序电流保护特性由于与负载故障特性相似,即故障电流越大,动作时间越小,在系统运行方式变化较大时也能自动配合,在很多场合下比定时限零序电流保护性能更为优越[12-19]。
传统反时限零序电流保护整定配合原则存在局限性:如果各处保护分别按选择性配合的要求进行整定,则计算过程繁琐复杂;如果全网采用统一的反时限特性公式和时间常数,则难以满足保护选择性的要求[20-24]。针对此问题,本文提出了一种引入电压变速因子的反时限零序电流保护,与修正的反时限特性曲线相配合,可以大大简化反时限零序电流保护的整定计算,同时使上下级反时限零序电流保护动作时间自动配合,并提高保护动作的选择性。
1 反时限零序电流保护的实现
1.1 反时限特性方程
根据国际电工委员会IEC 255-3的规定,常用反时限特征有一般反时限、非常反时限和极端反时限。反时限特性方程通用表达式为
(1)
式中:t为反时限动作时间;tp为时间常数;I*为保护处测得的故障电流与启动电流比值(电流标幺值);α和β为反时限特性参数,α和β共同决定反时限类型,取值见表1。对于不同保护的特性曲线,保护动作时间均随流过保护装置电流增大而减小。工程应用中,依据实际情况选取适合的反时限曲线。
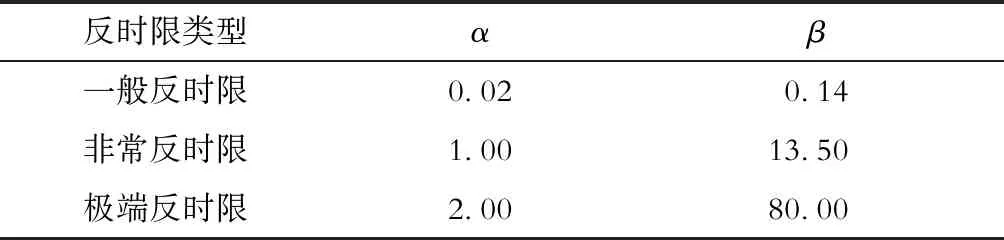
表1 不同反时限类型的α和β值Tab.1 Values of α and β in different curves
1.2 断线判据反时限零序电流保护的整定配合
本文以一般反时限为研究对象。由文献[16]可得,反时限保护的整定配合关系如图1所示。图1中,A、B、C、D为母线处,1、2、3为保护安装处,K1、K2、K3、K4、Ka、Kb为故障点,l为线路长度,te1为保护1在本段线路末端故障时动作时间,ts2为保护2在本段线路首端故障时动作时间,te2为保护2在本段线路末端故障时动作时间,ts3为保护3在本段线路首端故障时动作时间,te3为保护3在本段线路末端故障时动作时间,Δt为本段保护末端故障时和下一段保护首端故障时动作时间差,tⅡ为定时限Ⅱ段保护动作时间,Δt1为本段定时限Ⅱ段保护范围内末端故障动作时间与下一段反时限保护动作时间差,Δt2为本段定时限Ⅱ段保护范围内首端故障动作时间与上一段反时限保护动作时间差。
由图1(a)可知,保护上下级反时限特性曲线需逐级整定,即:首先整定末端曲线3(勿需与下级保护配合);其次在保护3开口故障时,以曲线3得出的动作时间ts3叠加上动作时间差Δt,即以ts3+Δt整定曲线2;曲线1的整定以此类推。
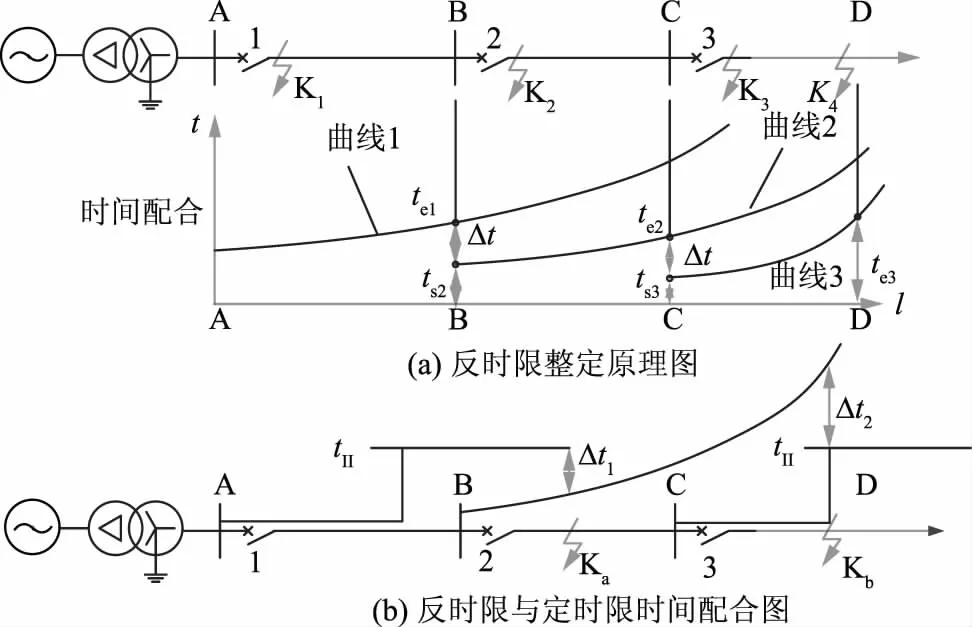
图1 反时限保护整定配合Fig.1 Setting and coordinating diagram of the inverse time protection
由图1(b)可知,以保护2反时限特性为例,定时限保护和反时限反时限保护时间配合要求:在各种运行方式下,保护1定时限Ⅱ段末端Ka故障时,需满足式(2);保护2定时限Ⅱ段首端Kb故障时,需满足式(3)。
(2)
(3)
式中:Ik1为Ka故障时流过保护2的电流;Ik2为Kb故障时流过保护2的电流。
对于1组确定的反时限曲线,相应的短路电流是否满足式(2)、(3),会出现以下4种情况:
a)式(2)、(3)均满足,反时限零序电流保护整定配合统一性满足;
b)式(2)满足,式(3)不满足,则反时限零序电流保护的时间常数偏小,增大最后一级线路末端的最小动作时间ten设定值(如图1中增大te3);
c)式(2)不满足,式(3)满足,则反时限零序电流保护的时间常数偏大,适当减小最后一级线路末端的最小动作时间ten设定值;
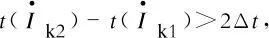
由此可见,传统反时限零序电流保护整定原则以及定、反时限保护的配合要求,虽然理论上可以很好地满足继电保护选择性的要求,但在实施中可能出现相互矛盾的情况。
1.3 反时限零序电流保护的工程应用
通过第1.2节的分析可知,反时限零序电流保护的局限在于:全网统一整定的计算过程繁琐复杂,灵活性差,有时甚至难以同时满足保护上下级时间配合与定、反时限保护时间配合的要求。为此,南方电网在反时限零序电流保护的应用中,不仅将启动电流Ip设定为统一值(300 A),也将时间常数tp设定为全网统一值(1.0 s),并且不考虑定、反时限时间配合问题。
220 kV以上电压等级系统的变电站通常都连接着接地变压器,母线接地变压器的分流作用使故障线路的零序电流大于非故障线路的零序电流;因此,即使采用相同的时间参数,下级保护的动作时间也快于上级保护时间,可以实现保护上下级之间的自然配合。尽管如此,保护的上下级动作时间配合完全依赖于母线接地变压器的分流,在某些特定条件下不能很好地满足保护的选择性,如母线接地变压器检修退出运行,即使不考虑定、反时限时间配合问题,也将给保护动作的可靠性和选择性带来挑战。
2 引入电压变速因子的反时限零序电流保护
中性点接地系统中发生不对称接地故障时,故障点零序电压最高,越远离故障点,零序电压越低。基于这一特点定义电压变速因子
(4)

将电压变速因子m引入式(1)特性方程的分母中,可以对现有的反时限零序电流保护进行改造,使其在全网采用统一的反时限特性及时间常数的条件下保证保护上下级拥有足够动作时间差,更好地满足保护的选择性与可靠性要求。
2.1 电压变速因子特性分析
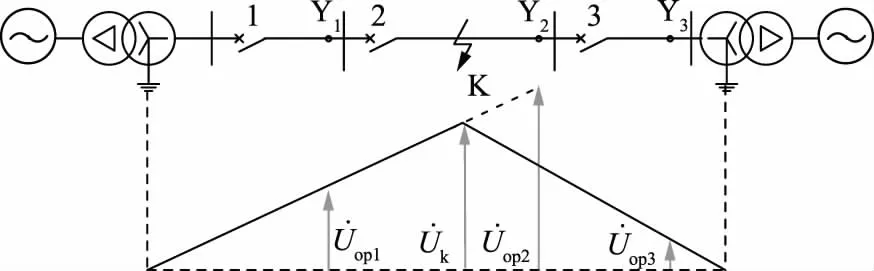
图2 发生不对称故障时的电压分布Fig.2 Voltage distribution with asymmetric fault
因此,将m引入反时限特性方程,可以实现保护区内故障加速、区外故障减速,保护出口附近故障时甚至可以瞬时切除故障。区外较远处故障时,由于电压变速因子m的修正,动作时间大大增加甚至不动作,可能造成下级保护失去远后备,但这可以通过修正电压变速因子引入方式进行纠正。
2.2 电压变速因子参数
(5)
若故障类型为单相接地故障,则
(6)
若故障类型为两相接地故障,则
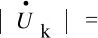
(7)
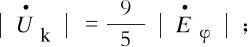
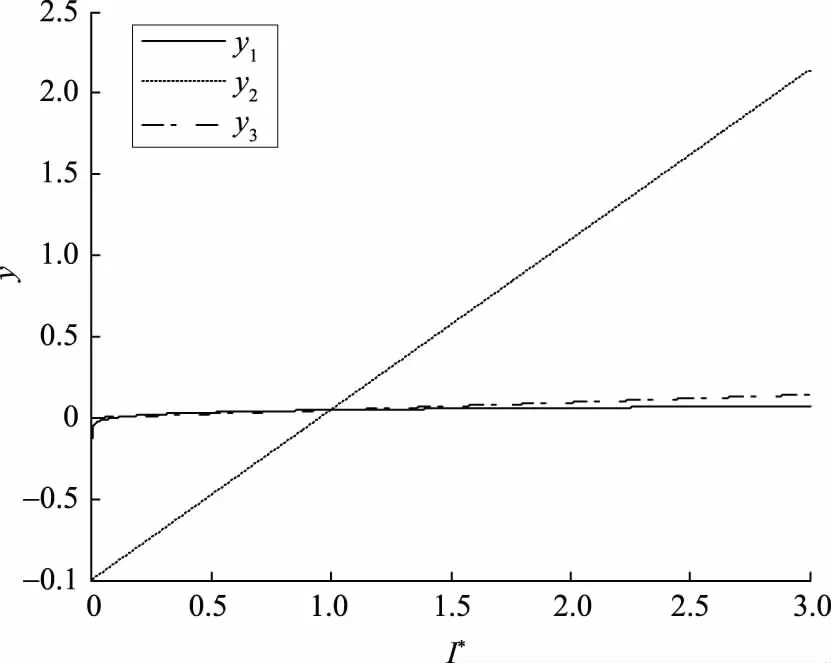
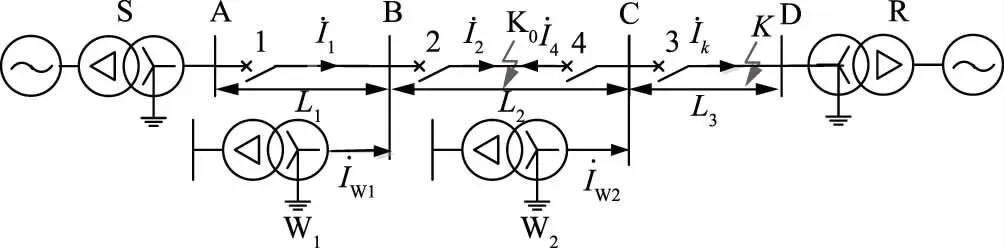
补偿电压的整定阻抗Zset的大小决定区内故障的划定范围,以本线路阻抗ZL为基准,分为3种情形,即Zset>ZL、Zset=ZL或Zset (8) (9) 式(8)、(9)中:ZS为系统阻抗;ZL1为保护1所在线路阻抗;Zset2、Zset2分别为保护1、2补偿电压整定阻抗。 表 2列举了m引入反时限方程的3种方式。 表2 电压变速因子m的引入方式Tab.2 Introducing way of voltage factor m 对电压变速因子不同的引入方式进行数学分析,结果如图3所示,其中y1、y2、y3为采用不同电压变速因子m引入方式时反时限动作方程分母值(见表2),y1=(mI*)0.02-1、y2=m(I*)0.02-1、y3=m[(I*)0.02-1]。 图3 y1、y2、y3随m变化曲线Fig.3 Changing curves of y1、y2、y3 with m 由图3可知:m>1时,max{y1,y2,y3}=y2,即“修正电流幂函数”的引入方式对反时限零序电流保护加速程度最大;m<1时,y1、y2均可能出现小于0的情况。 从希望故障快速切除的角度出发,选用“修正电流幂函数”的引入方式;从保证动作时间为非负的角度出发,选用“修正动作时间”的引入方式。通过数学分析可知:若选用“修正电流幂函数”的引入方式,上级保护m>1时,会使上下级保护的动作时间差减少,不利于保护的选择性动作;而选用“修正动作时间”的引入方式,既能对保护进行加速,又能增加保护上下级动作时间差,最终选用此种引入方式。 电力系统的短路一般不是金属性的,而是在短路点存在过渡电阻。 单相接地故障时,式(6)可改写为 (10) 式中Rg为过渡电阻。 同理,两相接地故障时,式(7)可改写为 (11) 考虑母线接地变压器的影响,将如图4所示的多级线路相连的输电线路在PSCAD中建立模型仿真,其中,ZS1、ZS0为送端系统正负序阻抗,ZR1、ZR0为受端系统正负序阻抗,Ip为启动电流,W1、W2为母线接地变压器,IW1、IW2为流过变压器的电流。送电端系统:ZS1=j23 Ω,ZS0=j40 Ω;受电端系统:ZR1=j56 Ω,ZR0=j115 Ω;两侧电势功角δ为30°。输电线路:正、负序阻抗相等ZL1=ZL2=(0.018 39+j0.263 9) Ω/km,零序阻抗ZL0=(0.141 3+j0.602 7) Ω/km。变压器额定容量100 MVA,电压500 kV,W1、W2短路占比为10%、50%。保护1、2、3所在线路长度L1、L2、L3分别为20 km、100 km、50 km。tp=0.5 s,Ip=300 A,Zset=0.85ZL。 图4 多级线路相连的输电线路Fig.4 Transmission line of multistage lines connected 保护3所在线路发生A相接地故障时的反时限时间特性如图5(Rg=0 Ω)、图6(Rg=100 Ω)所示,图5中U1、U2、U3分别为3种保护的测量电压。 图5 保护3所在线路A相接地故障时的反时限特性(Rg=0 Ω)Fig.5 Inverse time characteristicof protection 3 with A-G fault (Rg=0 Ω) 图6 保护3所在线路A相接地故障时的反时限时间特性(Rg=100 Ω)Fig.6 Inverse time characteristicof protection 3 with A-G fault (Rg=100 Ω) 由图6可以看出,当过渡电阻较大时,引入电压变速因子对反时限动作时间的修正作用较小。但方案设定m<1时,不对保护时间进行修正,因此不会对原有保护造成负面影响。 a)现有的反时限零序电流保护在工程应用上存在严重的局限性,如果各处保护分别按选择性配合的要求进行整定,则计算过程繁琐复杂;如果全网采用统一的反时限特性公式和时间常数,又难以满足保护选择性的要求。 b)提出了一种引入电压变速因子的反时限零序电流保护,通过分析电压变速因子的特性、参数和引入方式,详细阐述了该方案的具体应用。分析表明:该方案既能简化反时限零序电流保护的整定配合,又能较好地保证保护的选择性和速动性。 c)分析了过渡电阻对修正保护方案的影响,即高阻接地故障时,保护动作的速动性将受到挑战。对保护方案进一步优化,扩大变速因子的加速范围,并设定只有当电压变速因子m>1时,才引入m,对反时限保护只加速不减速,以达到躲高阻接地故障的目的,确保电压变速因子的引入不会对原有的反时限保护造成负面影响。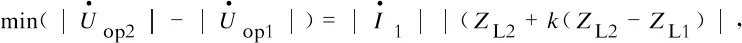
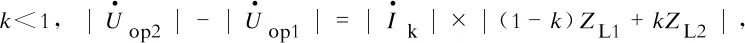
2.3 电压变速因子的引入方式

3 过渡电阻的影响及其对策
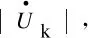


4 仿真验证

5 结论
