大失准角下SINS的KF/EKF2混合滤波对准

赵彦明，秦永元

(西北工业大学 自动化学院,陕西 西安 710129)

0 引言

捷联惯导系统(SINS)导航精度在很大程度上依赖初始对准精度[1]。传统的初始对准方法是利用静基座下重力加速度和地球自转角速率信息先完成粗对准[2]，再进行精对准。对于低精度惯导系统或系泊状态下舰载惯导系统粗对准误差较大，精对准是在大失准角条件下进行的。此时，SINS误差模型呈现强非线性，标准卡尔曼滤波(KF)不再适用，需要采用非线性模型和非线性滤波算法[2]。

针对大失准角条件下SINS对准问题，文献[2]提出了一种基于二阶非线性量测的二阶扩展卡尔曼滤波(EKF2)算法，可以在任意姿态条件下进行初始对准。文献[3]将容积卡尔曼滤波法(CKF)应用于SINS非线性初始对准中，提高初始对准精度。文献[4]提出了一种基于快速正交搜索(FOS)和KF的非线性参数估计方法。文献[5-6]给出了大失准角条件下的非线性对准模型，通过无迹卡尔曼滤波(UKF)完成精对准。文献[7]提出了一种改进的采用类高斯和重采样的粒子滤波算法(PF)，可以在大失准角的非线性、非高斯状态下完成精对准。文献[8]采用变换无迹求积卡尔曼滤波(TUKF)进行了噪声不确定和大失准角条件下SINS对准实验，结果显示滤波算法具有高精度、快速性和鲁棒性。目前的大失准角对准所采用的全状态非线性滤波具有滤波维数大、算法复杂、计算量大等缺点[9]。

本文提出了一种基于模型分解的KF/EKF2混合滤波方法，将基于欧拉平台误差角的非线性滤波模型分解为非线性部分和线性部分，分别采用EKF2滤波和KF滤波进行处理。实验结果表明，该方法可以有效减小计算量，改进实时性和稳定性。

1 非线性滤波对准模型

1.1 大失准角下SINS误差模型

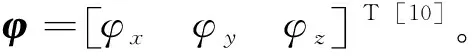
(1)

(2)

(3)

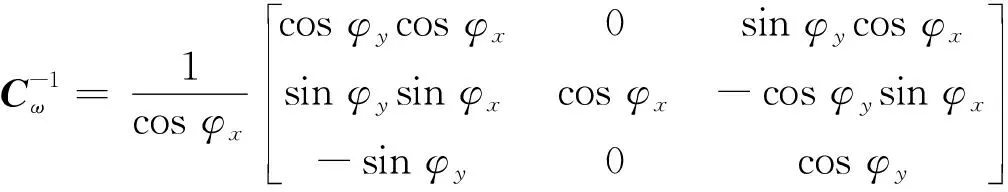
(4)

式中i=x,y,z。

1.2 准静基座大失准角初始对准滤波模型

对于IMU器件误差，将陀螺常值漂移和加速度计常值零偏扩充到系统状态中，状态向量选为

(5)

式中δvn为地理坐标系下速度误差向量。

结合式(1)、(2)可得用于非线性滤波的系统方程：

(6)

(7)

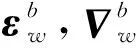
(8)

(9)

以SINS的速度输出作为观测量，则量测方程为

(10)

2 非线性滤波模型分解

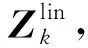
Glin(t)wlin(t)

(11)

(12)

(13)

(14)

(15)

(16)

式中gn为应力加速度矢量。

2) 非线性部分滤波模型。从式(6)中分离出状态非线性部分，整理可得非线性部分状态方程；而非线性部分量测向量为

(17)

可以分离出非线性部分的滤波模型：

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

3 KF/EKF2混合滤波算法

基于模型分解的KF/EKF2混合滤波过程如下：

KF滤波递推方程可参照文献[11]，重点将介绍非线性部分的EKF2滤波。

1) EKF2时间更新。非线性部分状态维数l=3，量测维数m=3。则非线性部分的EKF2时间更新公式如下：

(26)

(27)

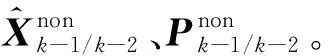
2) EKF2量测更新。由于非线性部分滤波模型的量测方程是线性的，所以EKF2量测更新与KF量测更新相同，具体算法见文献[11]。

4 仿真实验验证

4.1 仿真条件

为了分析滤波算法的性能，预设精对准初始误差和器件误差，生成航迹数据，采用蒙特卡洛(Monte-Carlo)仿真方法对KF/EKF2混合滤波精对准算法进行仿真，且与EKF2、UKF算法进行对比。

仿真条件：

1) 载体的位置为经度108.9 °，纬度34.2°，高度400 m；速度为0；三轴姿态设置为10°，0°，-180°。

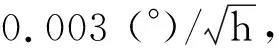
3) 在Monte-Carlo仿真中，初始失准角设置：俯仰和横滚角初始失准角服从[-20°,20°]区间上的均匀分布，方位角初始失准角服从[-40°,40°]上的均匀分布，共进行20次Monte-Carlo仿真，每次仿真时间为300 s。

4) 速度量测噪声设置为0.05 m/s，滤波周期设置为1 s，并对惯导速度、姿态进行反馈校正。对准精度用反馈校正后的姿态与真实姿态之差进行评估。

4.2 实验结果

图1～3分别为KF/EKF2混合滤波对准俯仰角误差(δφx)、横滚角误差(δφy)和方位角误差(δφz)。从图1～3可看出，KF/EKF2滤波对准的水平失准角收敛很快，方位误差角在150 s内收敛。达到滤波稳态后，KF/EKF2混合滤波精度为[0.004 37°, -0.005 186°, 0.105°]，接近静基座小失准角KF精对准的极限精度。

图1 KF/EKF2混合滤波俯仰角误差

图2 KF/EKF2混合滤波横滚角误差

图3 KF/EKF2混合滤波方位角误差

为了与传统全误差状态非线性滤波对准进行比较，文章分别用KF/EKF2混合滤波，全状态EKF2滤波、全状态UKF滤波进行仿真测试，统计3种方法对准误差的均方根值(RMS)，如表1所示。3种方法稳态精度接近，KF/EKF2和EKF2滤波的对准精度略优于UKF，KF/EKF2和EKF2滤波的精度相当。

表1 对准误差RMS统计对比

在CPU为Intel双核i5@2.6 GHz、4 GB内存的笔记本电脑上运行Matlab仿真程序，经测算KF/EKF2混合滤波算法单次平均滤波时间为14.701 ms(即滤波程序块的单次运行时间)，EKF2算法单次平均滤波时间为25.062 ms，UKF算法单次平均滤波时间为23.059 ms。可见KF/EKF2混合滤波的实时性更好。

综上仿真结果表明，KF/EKF2混合滤波对准的综合性能指标优于全状态EKF2、UKF等非线性滤波对准算法。

5 结束语

在惯性器件精度很差或强干扰条件下，SINS系统误差模型可能呈现强非线性，标准KF不再适用，需要采用非线性误差传播方程和非线性滤波算法(其中EKF2和UKF滤波最常用)。但非线性滤波算法存在计算量随着状态维数增加而急剧增大的问题，影响滤波稳定性和实时性。为了降低非线性滤波状态维数，减小计算量，本文提出了一种基于状态空间模型分解的KF/EKF2混合滤波方法，并且对其进行了蒙特卡洛仿真验证。实验结果证明， KF/EKF2混合滤波算法在计算量、实时性和对准精度等方面综合优于EKF2滤波和UKF滤波。