行波型球形超声电机定子的优化设计

郭 语，陆 庆，孙志峻，宋爱国

(1.东南大学 仪器科学与工程学院，江苏 南京 210096；2.金陵科技学院 机电工程学院，江苏 南京 211169；3.南京航空航天大学 机械结构动力学与控制国家重点实验室，江苏 南京 210016)

0 引言

球形超声电机是一种多自由度超声电机，因其具有响应快，定位精度高，断电自锁，抗干扰能力强及结构简单，易集成化等优点，受到越来越多的关注。它具有类似于球关节的结构形式，非常适合应用于机器人关节、人工眼球等领域，许多研究学者从不同结构形式、驱动控制机理和应用方式对其开展了相关研究。

球形超声电机的转子一般为球形，定子可采用不同的结构形式和激励方式。MASHIMO等[1]提出了一种3个环形行波定子共同夹持驱动1个球转子的球形超声电机，但尺寸和输出力矩较小。TING等[2]将一系列弯曲压电陶瓷沿半球形定子表面直线布置，通过在相邻压电陶瓷上施加适当的相位差分电压信号，在定子上产生行波并驱动球转子的多自由度运动。LU等[3]提出了一种三明治结构的多自由度球形超声电机，利用两个压电振子夹持1个球转子，利用定子激发出的5个振动模态使球转子具有3个转动自由度。赵淳生等[4]针对圆柱-球体多自由度超声电机的定子进行优化设计，保证定子的一阶纵振和二阶弯振的固有频率基本一致。张健滔等[5]提出了一种利用二阶面内振动模态工作的多自由度驻波超声电机，可实现球转子的3个转动自由度，但定、转子间的预压力仅通过球转子的自身重力提供，因此具有一定的应用局限性。SHI等[6]研制了一种面向人工眼球应用的球形超声电机，利用复合定子激发的轴向弯曲模态和面内非轴对称模态，通过4个驱动足产生的3种椭圆运动使球转子具有3个旋转自由度。王剑等[7]基于柔性板簧设计的三自由度球形超声电机具有多定子与球转子之间的自适应对心调节能力。

本文提出一种具有同步调心底座的球形超声电机，由3个环形行波型定子共同夹持驱动1个球转子，采用类似三爪卡盘的面螺纹机构实现3个定子的同步调心。利用有限元仿真软件对定子进行动力学分析与优化设计，对定子试制件进行了定扫频实验。

1 球形超声电机的结构与工作原理

球形超声电机主要由三爪卡盘底座、定子及其支架、球转子组成(见图1)。球转子被3个定子夹持，3个定子及其支架水平圆周均匀分布，每个支架内装有碟形弹簧、微型压力传感器等零部件，微型压力传感器用以检测定、转子间的预压力。现有采用类似结构的球形超声电机需要单独调节定子支架以改变预压力，操作繁琐且难以保证调节过程中转子球心的位置精度，本文采用的三爪卡盘底座在保证3个定子与球转子预压力同步调节的同时，实现转子的自定心。

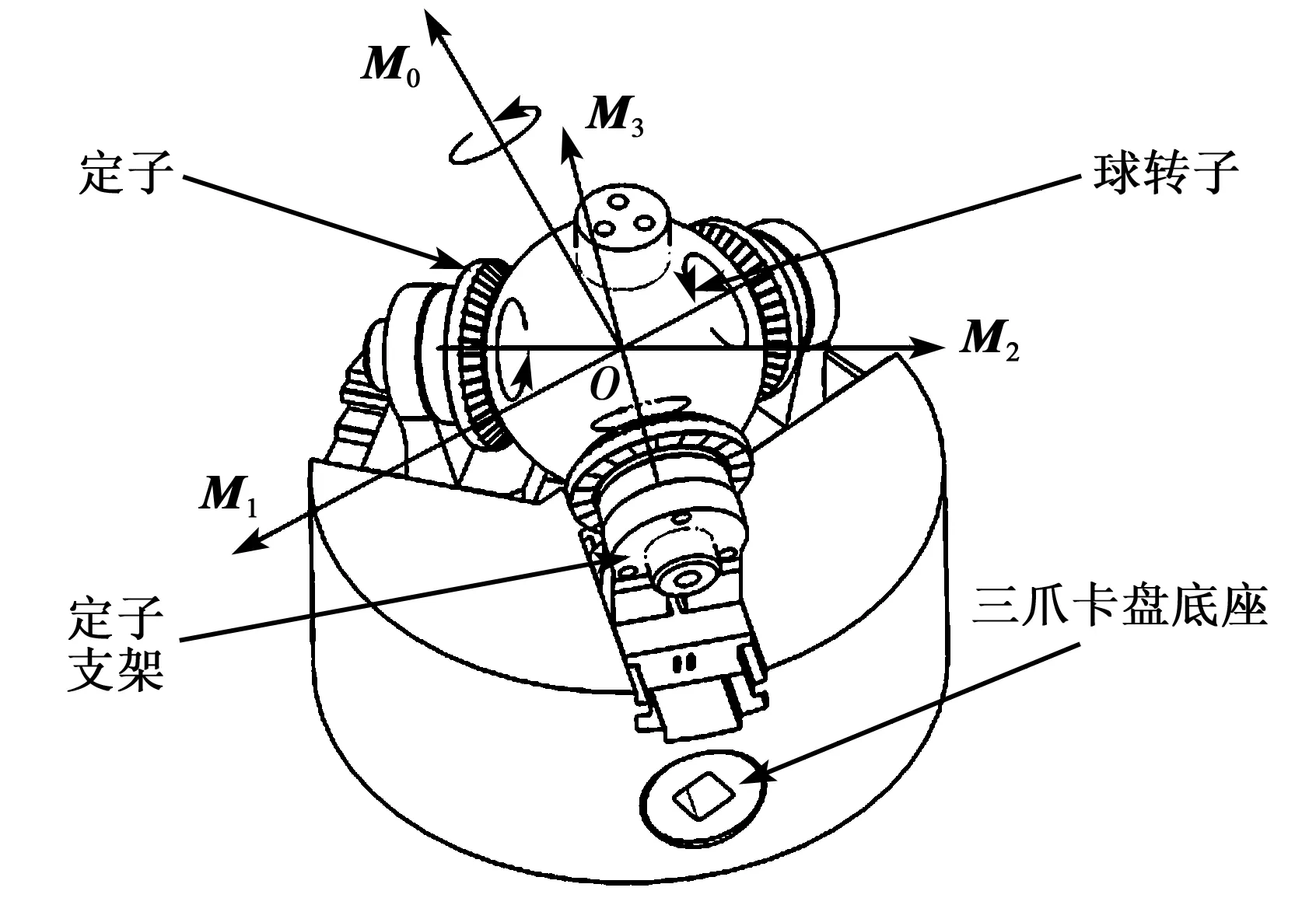
图1 球形超声电机结构

3个定子在与球转子接触位置作用有3个驱动力矩矢，分别为M1、M2、M3，3个力矩矢相交于球心处，根据矢量合成关系，可以合成为一个过球心的合力矩矢M0。通过改变3个超声电机定子的驱动作用，即改变M1、M2、M3的大小，从而在三维空间中改变M0的方向和大小，使球转子绕M0的方向转动。图2为1号定子与球转子的安装结构示意图。定子中心轴线与水平面夹角为α，则球转子所受的M0与M1、M2、M3之间的关系为

(1)

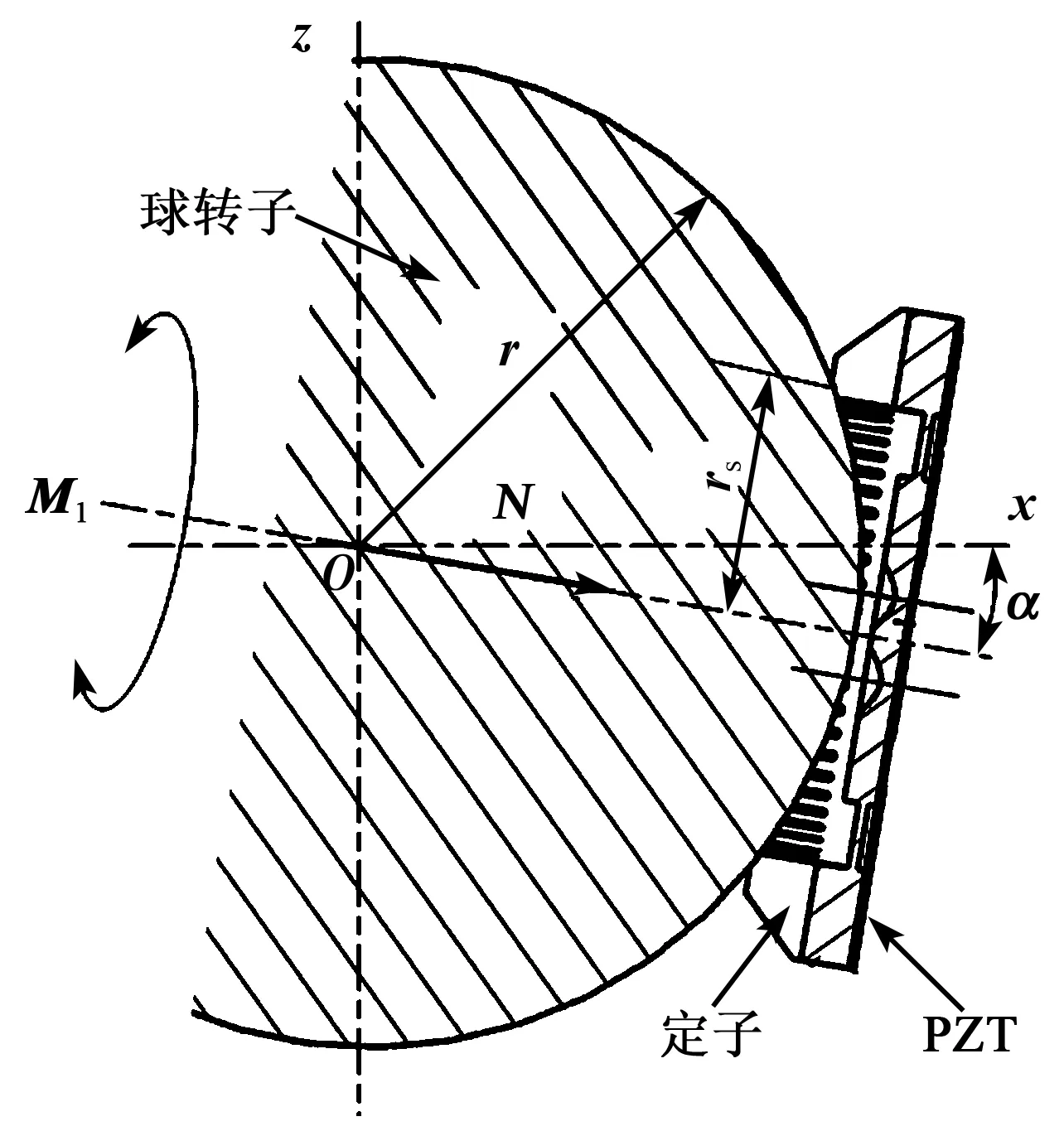
图2 单定转子安装结构

每个定子与球转子的接触部位为定子内缘一狭窄圆环面，设接触圆半径为rs，球转子半径为r，预压力为N，μ为定、转子间的摩擦系数，则第i个定子对球转子的理想驱动力矩为

(2)

考虑带载驱动时，定、转子间接触的粘滑效应，实际驱动力矩为

(3)

式中:ωsi为第i个定子表面质点椭圆运动的平均切向速度对应的转子角速度；ωri为实际球转子角速度矢量在第i个定子中心轴上的投影大小；cdi为第i个定、转子间和相对速度有关的动态库伦摩擦系数，由于接触力学的非线性，难以确定实际值。式(1)、(3)表明，球形超声电机的输出力矩主要受单个定子的性能及定、转子间的接触力学影响。由于定、转子间接触力学的非线性和复杂性，因此，本文主要通过对定子的优化设计提高球形超声电机的性能。

2 定子的优化设计

2.1 行波型定子的结构参数化

本文设计的球形超声电机定子为圆环结构，由锡青铜材质的金属基体和d33效应的PZT-4压电陶瓷组成。由于圆环结构具有轴对称性，因此，定子存在两相同频正交模态。在环形定子底部黏贴有两相极化分区的压电陶瓷片，通过施加空间与时间上分别相差1/4波长和周期的激励电压，激起定子弹性体的行波，从而使定子表面质点产生椭圆运动，在摩擦力的作用下驱动球转子转动。本文选择B07模态作为定子的工作模态，齿数定为工作模态中行波数的整数倍，以保证不同驱动点速度方向的一致性。该模态有7个波，因此齿数定为42，是波数的6倍。定子基体的参数化尺寸如图3所示，中间圆板通过3个螺纹孔与固定支架连接。为了减小固支对圆环振动体的影响，中间圆板和圆环振动体之间的连接厚度小于1 mm。圆环振动体上开有齿槽形成一定高度的齿，用来提高定子的驱动效果。图3中，h为总高，R为外环半径，h1为固定板厚度，p1为连接板厚度，p2为齿高，p3为齿宽，p4为齿槽宽，p5为齿外缘斜角。

图3 定子参数化结构

不同于常规圆环形行波超声电机定子主要依靠上端面实现驱动圆板转子，该定子通过其内缘的狭窄圆环面驱动球转子，因此多出p5这一结构参数。h、h1和R根据外形尺寸及定、转子间的安装关系确定并为固定值，在确定优化参数变化范围且应保证各参数变动时，结构内不产生干涉、尺寸负值等现象，固定尺寸和初定各优化参数初值及其范围如表1所示。

表1 固定尺寸、优化参数初值及其取值范围

2.2 定子的结构有限元分析

定子能否正常工作且满足性能要求，取决于以下几方面因素：

1) 工作模态是否远离干扰模态。

2) A、B两相频率是否一致。

3) 定子弹性体表面所激发行波的振幅和形态是否理想。因此，需要对环型定子进行模态分析以确定其工作模态和谐振频率，同时通过结构参数的调整，使工作模态与干扰模态尽量远离，这是超声电机设计中的关键。

4) 通过谐响应分析可以确定工作模态频率激励下产生的最大振幅。利用有限元软件对超声电机定子进行结构分析是目前最常用的手段。定子材料的相关属性如表2所示。

表2 定子材料主要参数

在ANSYS中建立初始参数尺寸的定子模型，划分网格、设置边界条件(内圈3个沉头孔施加固定约束、外圈自由)后进行模态分析，解算得到前100阶定子模态的频率和振型，并从中筛选出B07模态及其邻近模态，如表3所示。

表3 B07模态及其邻近模态

研究表明，工作模态与干扰模态频率相差大于2 kHz，干扰模态不会影响电机的正常工作[8]。根据模态分析结果，工作模态的两个简并模态共振频率较一致，和相邻前1阶干扰模态频率差仅有782 Hz，和后1阶干扰模态频率约有1.2 kHz的差值，易产生模态混叠，影响定子的工作性能。因此，需要对环形定子的结构进行优化，使其工作模态尽量远离干扰模态。

在对定子进行模态分析后，通过谐响应分析可检验定子在工作频率附近的简谐电压激励下的振幅大小，即定子的幅频特性。在谐响应分析中需添加压电陶瓷的压电耦合关系，其压电本构方程为[9]

T=cES-eE

(4)

D=eTS+εSE

(5)

式中：T为应力张量;D为电场强度张量;S为应变张量;E为电场强度张量;cE为恒电场下的弹性系数矩阵;e为压电常数矩阵;εS为介电常数矩阵。利用ANSYS软件模拟压电陶瓷驱动定子系统动力学方程为[10]

(6)

式中：Qu为节点位移矢量;Qφ为节点电势矢量;M为质量矩阵;Cs为单元结构阻尼矩阵;Cd为单元介电阻尼矩阵;Ks为刚度矩阵;Kd为介电常数系数矩阵;Kp为压电耦合矩阵;Fu为节点力矢量;Fφ为电荷矢量。对压电陶瓷施加激励电压峰-峰值为120 V，根据表3的数据，频率设为44～47 kHz，得到定子系统的幅频特性曲线，如图4所示。

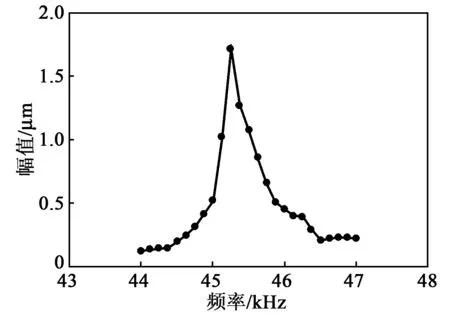
图4 定子系统幅频特性

由图4可知，定子驱动面的最大响应振幅约为1.7 μm。根据定子表面质点周向位移函数[2]：

uc(x)=(πWh0/λ)cos(ωt-nx)

(7)

式(7)对时间求导可得定子周向速度函数：

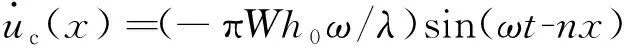
(8)

式中:W为纵向振幅;h0为定子弹性体基板厚度;λ为振动波长;ω为角频率;n为波数。式(8)表明，如果定子振幅较小，会造成周向速度低，纵向振幅过小甚至可能出现无法克服转子表面粗糙度而停转。因此，在进一步的优化设计中，需要尽量提高定子振幅。

2.3 定子结构的优化设计

超声电机定子的设计通常采用参数分析法，这种方法是一种试误法，需要较多时间来寻找合适的参数集。如果输入参数很多，那么要检查的配置数量可能非常庞大，且设计结果是次优的[11]。

响应面法是获得给定目标随输入参数变化的有效方法，在给定输入变量上提供性能的连续变化，精度可控制，有利于进一步优化。基于响应面法的优化设计原理是：首先确定每个设计变量的合理变化范围(设计空间)，利用概率采样挑选设计空间中的若干点并建立响应面模型(最佳拟合面)，最后采用优化算法进行全局优化[12]。

根据前述分析，确定定子设计的两个优化目标：

1) 工作模态频率尽量远离相邻干扰模态频率。

2) 定子表面质点振幅最大。

为了更有效地进行优化设计，在确定最终设计变量前应进行结构参数的灵敏度分析，以确定影响定子优化目标的关键因素。结合模态分析和谐响应分析结果及表1中所列参数，5个设计参数分别对定子振幅、工作模态频率、干扰模态频率1(相邻前1阶)、干扰模态频率2(相邻后1阶)的灵敏度分析结果如图5所示。

图5 设计参数的灵敏度

由图5可知，p1对振幅、工作模态频率和干扰模态频率2的灵敏度都较低。p2对振幅和模态频率的灵敏度都很高，且对工作模态的灵敏度高于干扰模态。p3对振幅和干扰模态频率1的灵敏度比工作模态频率和干扰模态频率2大，而p4对振幅的灵敏度较模态频率略大，p5对振幅的灵敏度较低，但对模态频率灵敏度有一定贡献。根据以上现象，最终的设计变量排除p1，保留p2、p3、p4和p5。建立对应的两个优化目标函数，为使目标函数尺度接近，进行了比例缩放并转换为无量纲数。

(9)

(10)

式中：Fw、Ff、Fb分别为工作模态频率、前1阶干扰模态频率、后1阶干扰模态频率。设定工作频率为40～48 kHz，则最终的优化模型为

(11)

采用非参数回归法建立优化参数的响应面模型，利用稀疏网格自适应加密抽取采样点，最终得到设计变量与目标响应的响应面模型。选取灵敏度较高的两个参数p2、p3分别对应G1、G2的响应面如图6所示。响应面的拟合质量可由误差决定系数反映，图6中的G1、G2响应面误差决定系数分别为98.93%和98.84%，表明所构造的响应面模型具有较高精度，可作为优化的近似对象模型。

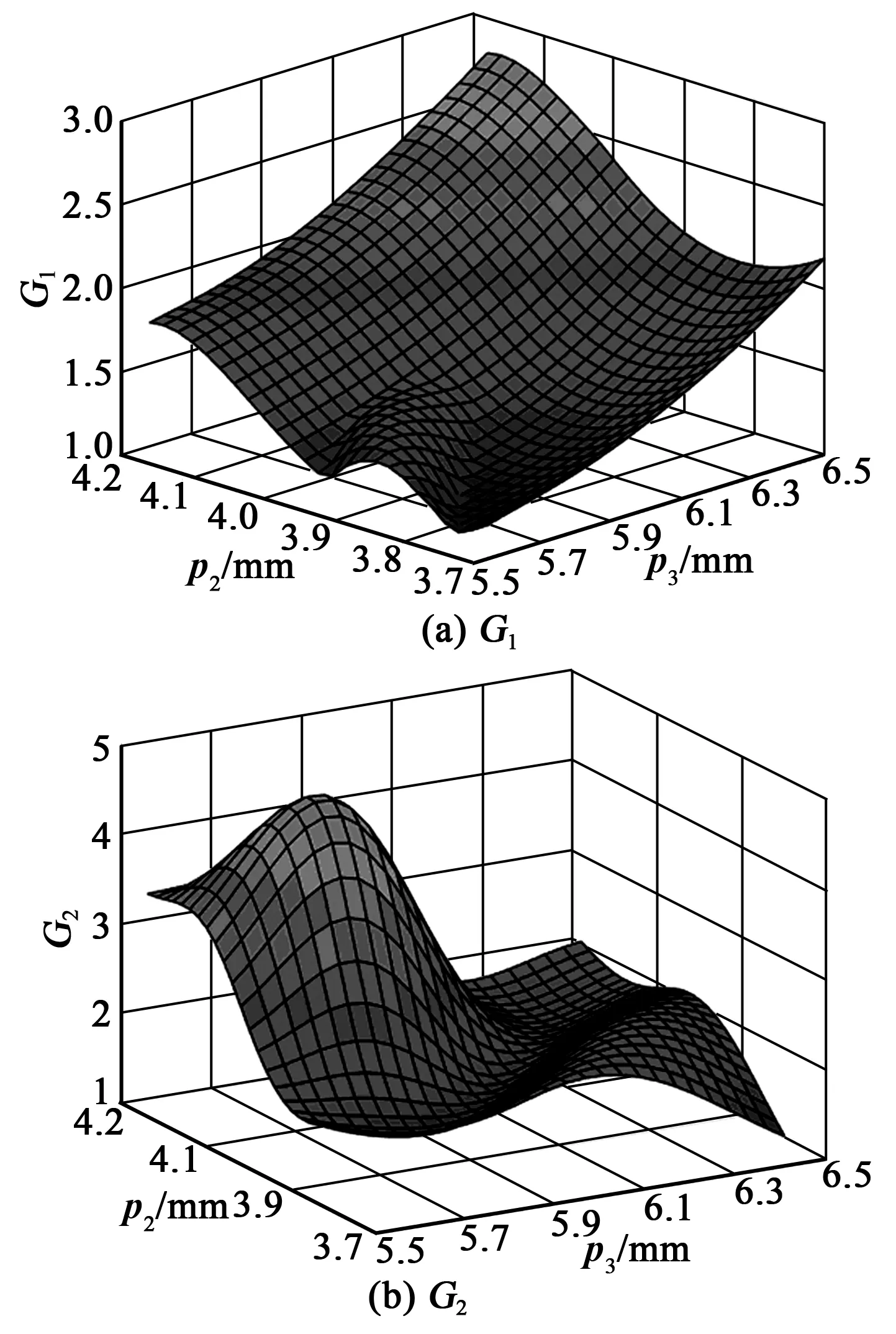
图6 部分结构参数对目标函数G1,G2的三维响应面

优化算法选择多优化目标的迭代遗传算法(MOGA)，该方法是一种全局优化算法，适合于多目标优化问题[13]。种群大小设置为100，最大进化代数取200。优化得到的Pareto前沿如图7所示。

图7 Pareto前沿

由图7可知，两个优化目标在较大范围内相互制约，需要根据不同的策略选择最终的非劣解。本文在选择优化结果时，以侧重模态分离为原则挑选优化参数，表4为优化前、后及修正结果的对比。

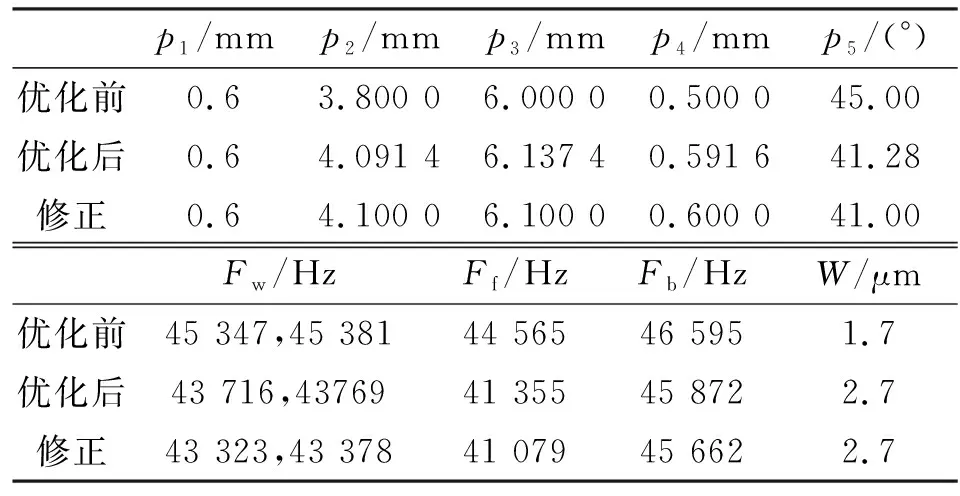
表4 优化前、后及修正结果对比

3 实验测试

试制了一个定子并黏贴好压电陶瓷片，利用二维激光测振仪对其进行定扫频实验，所加交变电压峰-峰值为120 V，电流为0.3 A，测试结果如图8所示。

图8 定子定扫频振动测试结果

由图8可知，定子B07模态A、B两相频率均为42.7 kHz，具有很好的模态一致性。定子纵向振幅约2.3 μm，具有良好的振动表现。模态频率值和有限元分析结果相差约0.6 kHz，误差较小。定频实验结果表明，在42.7 kHz频率下，均能激励出良好的A、B两相驻波，模态较纯，证明设计的定子结构合理可靠，可以产生良好的行波。

4 结束语

创新性的将三爪卡盘自动定心的特点应用在球形超声电机的夹持机构中。建立了单个定子对球形电机输出力矩的数学模型。运用有限元分析软件对定子结构参数进行灵敏度分析、模态分析和谐响应分析，并建立了基于响应面模型的多目标优化模型。优化结果成功实现了定子模态分离要求，并提高了表面振幅。定子试制件的定扫频实验测试结果也表明，本文设计定子所采用的优化方法是有效的，为多自由度球形超声电机的实现奠定了良好基础。