基于压电传感器的单一模态Lamb波损伤检测

周 凯，徐新生，武湛君

(大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024)

0 引言

超声兰姆(Lamb)波是一种在板类结构中传播的超声导波，它具有传播速度快,传播距离远及幅值衰减小等优点[1-2]，且Lamb波对结构整个壁厚上的损伤均较敏感[3]，故其可用于板类结构损伤快速检测中。

基于Lamb波的损伤检测技术已在金属和复合材料等板类结构中获得广泛的研究[4-5]，然而，由于Lamb波传播的多模态性，即在任意频率下至少有2个模态传播[6]，且结构损伤和边界都会反射Lamb波，导致实际的Lamb波信号由多个模态不同信号叠加形成，较复杂，因此，常用的Lamb波损伤检测技术需要基准信号[7-8]。由于外界温度、载荷和边界条件等因素均会对Lamb波基准信号造成影响，故对于某些工程问题难以提供准确的基准信号，这限制了Lamb波损伤检测技术的应用。

针对这个问题，本文提出了一种应用于板类结构的单一模态Lamb波无基准损伤检测方法，实验中通过单一模态Lamb波对铝板的损伤进行检测，从检测信号中识别出损伤反射信号，并根据损伤反射信号传播时间计算损伤与传感器的距离。对比实际距离，分析了由理论群速度与实验群速度不一致引起的计算误差，并提出一种改进的计算方法。

1 Lamb波传播特性

各向同性板类结构中的Lamb波包括对称Lamb波和反对称Lamb波，分别描述板的对称振动和反对称振动，其位移可统一为

u=g1(z)ei(kx-2πft)

(1)

w=ig3(z)ei(kx-2πft)

(2)

式中：g1,g3为位移沿壁厚分布规律的函数；z为板厚方向；u为面内位移；w为离面位移；x为波传播方向；k为波数；f为频率；t为时间。由式(1)，(2)可知，Lamb波沿x方向传播。对称和反对称Lamb波频率方程为

(3)

其中

(4)

(5)

式中:h为板厚的一半；λ，μ为拉梅常数；ρ为密度；式(3)中的上标+和-分别表示对称和反对称情况。

图1为根据频率方程计算得到厚3 mm的铝板群速度频散曲线。计算采用的铝板密度、弹性模量和泊松比分别为2 700 kg/m3、70 GPa和0.33。由图可知，在频率低于500 kHz时只有S0和A0模态存在，模态数较少，有利于实际应用。实际中常选取低频Lamb波对结构损伤进行检测。

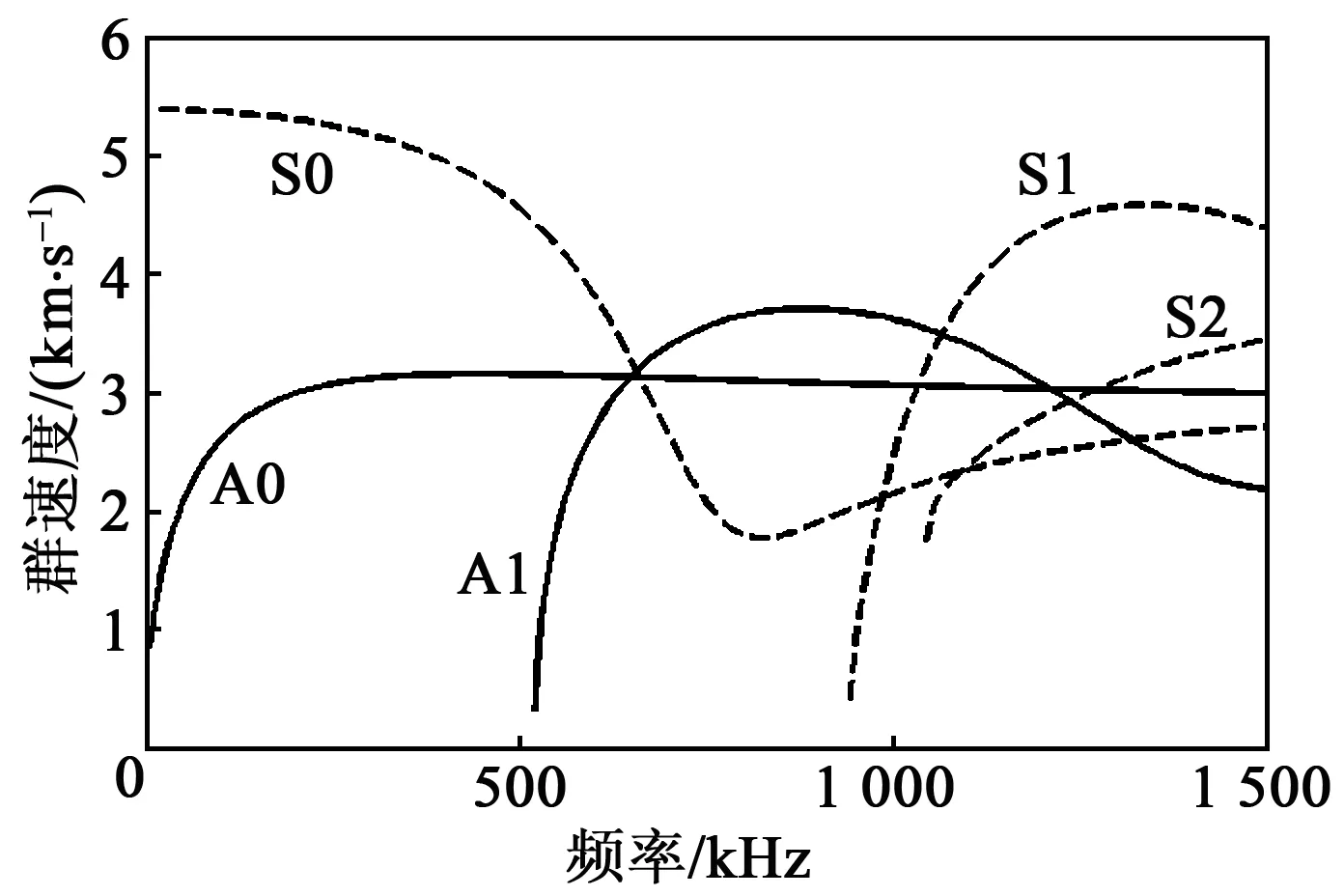
图1 壁厚3 mm的铝板群速度频散曲线

2 单一模态Lamb波损伤检测方法原理

基于单一模态Lamb波无基准损伤检测法是利用单一模态Lamb波对结构进行损伤检测，利用已知信息(传感器位置、边界等)判断检测信号中是否包含损伤反射回波，进而判断结构中是否存在损伤。若检测信号中包含损伤反射回波，可提取损伤反射回波传播时间，并根据损伤反射回波传播时间及对应的群速度计算损伤与传感器的距离。

3 铝板损伤检测方法

3.1 铝板损伤检测实验

图2 实验传感器及损伤位置图

3.2 单一模态Lamb波检测频率选取

传感器模型采用针应力模型[9]。采用表面粘贴的压电传感器激励Lamb波的应变幅值为[10]

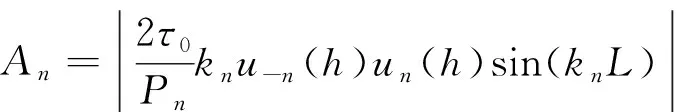
(6)

式中：A为幅值；P为与频率有关的因子；τ0为针应力载荷幅值；L为传感器长度的一半；n为模态，-n为沿反向传播的模态，即有k-n=-kn，此时，压电传感器粘贴于板上表面z=h处。

图3为在厚3 mm铝板中传感器激励的Lamb波各模态幅值随频率变化曲线。图中传感器长度为8 mm，铝板密度、弹性模量和泊松比与图1中一致，且对图中所示的Lamb波各模态幅值统一进行了归一化处理。由图可知，A0和S0模态幅值都随频率变化。低频时，激励的Lamb波是较单一的A0模态；在频率约为280 kHz时，激励的Lamb波为较单一的S0模态。实验中分别选取50 kHz和290 kHz作为单一模态损伤检测频率。

图3 在壁厚3 mm的铝板中各模态幅值随频率变化曲线

4 铝板损伤检测结果及讨论

4.1 损伤反射回波信号识别

图4分别为50 kHz、290 kHz和140 kHz频率下传感器接收到的Lamb波时域信号及包络图。图中D为含损伤板检测信号，S为损伤反射信号(含损伤板信号和无损伤板信号之差)，根据希尔伯特变换求得信号包络。由于传感器和边界位置已知，结合图1、3，可分别计算直达波和边界反射波理论传播时间，如表1所示。

图4 不同频率Lamb波时域信号及包络图

表1 直达波和边界反射波理论传播时间

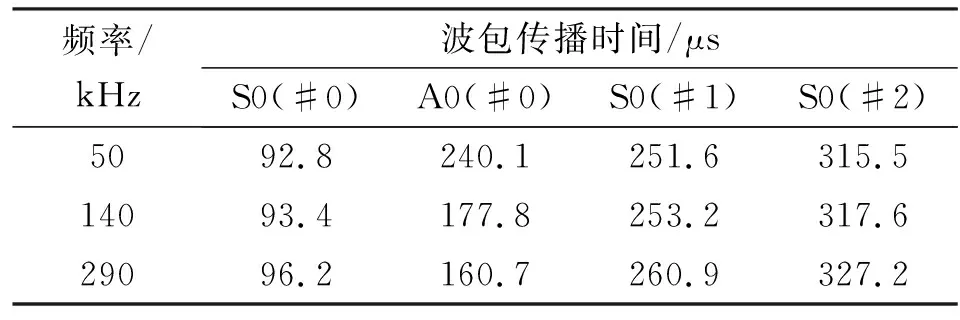
频率/kHz波包传播时间/μsS0(#0)A0(#0)S0(#1)S0(#2)5092.8240.1251.6315.514093.4177.8253.2317.629096.2160.7260.9327.2

表1中，S0(#0)表示直达S0模态，S0(#1)表示边界1反射S0模态，S0(#2)表示边界2反射S0模态，A0(#0)表示直达A0模态。波包传播时间根据对应频率下的群速度和传播距离计算得到，即

t1=l/vg

(7)

式中：t1为波包的理论传播时间；l为传播距离；vg为对应频率下的群速度。由于边界1、2反射的A0模态都超过了图4所示信号的时间范围，故不作考虑。图4中含损伤板检测信号中不同波包传播时间如表2所示，其中波包传播时间由波包的最大值对应的时刻及激励信号长度计算得到，即

t2=tmax-ts

(8)

式中:t2为实验中波包的传播时间;ts为激励信号时长的一半;tmax为波包最大值对应的时刻。

表2 含损伤板检测信号中不同波包传播时间

对比表1、2中传播时间可知，50 kHz时，波包1传播时间与直达A0模态和边界1反射S0模态较接近。根据图3可知，50 kHz下激励出的S0模态幅值较小，可忽略，此时可排除波包1是边界1反射的S0模态的情况，因此判断波包1是直达A0模态，波包2传播时间与直达和边界反射波都不符合，即判断其为损伤反射A0模态。290 kHz频率下波包1、3分别是直达S0模态和边界1反射的S0模态，波包2传播时间与直达A0模态较接近(相差约10%)。然而，根据图3可判断290 kHz下激励的A0模态可忽略，即可排除波包2是直达A0模态的情况，故可知波包2为损伤反射S0模态。频率为140 kHz时，压电传感器可同时激励出S0和A0模态，波包1～4分别被判断为直达S0模态、直达A0模态、边界1反射S0模态和边界2反射S0模态。

对比实际的损伤反射信号可知，在单模态(50 kHz和290 kHz)频率下，损伤反射回波及反射回波模态都被准确判断出来，但在140 kHz下,由于多模态的影响而产生了误判，S0和A0模态的损伤反射回波都未被识别出来。根据在50 kHz和290 kHz下单一模态检测信号判断结构中存在损伤，而根据在140 kHz下多模态信号判断结构中无损伤，这说明单一模态在这个方法中的优势。

4.2 损伤位置计算

根据损伤反射波传播时间可计算损伤与传感器的间距(ld)，直接利用理论群速度的计算方法为

ld=(vgtd-l)/2

(9)

式中:vg为群速度；td为损伤反射波传播时间。频率为50 kHz和290 kHz时损伤反射回波传播时间分别为425.4 μs和176.9 μs。通过式(9)计算得到ld分别为193 mm和209.5 mm，与实际ld(200 mm)之间的误差为3.5%和4.75%，引起误差的原因可能是实验中Lamb波的群速度与理论计算的Lamb波群速度不一致。为改进由群速度引起的误差，可利用直达波的传播时间对式(9)进行改进，即

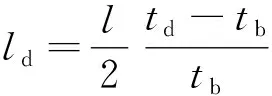
(10)

式中tb为直达波传播时间。根据式(10)可计算在50 kHz和290 kHz频率下ld分别为194.1 mm和198 mm，误差分别为2.95%和1%，均小于采用式(10)计算的误差。

5 结束语

针对板类结构，提出了一种基于单一模态Lamb波的无基准损伤检测法，并在铝板上进行损伤检测实验。根据压电传感器模型，选取50 kHz和290 kHz作为单一模态损伤检测频率，并分别从实际检测信号中识别出损伤反射回波。对比140 kHz下多模态情况，论证了单一模态在这个方法中的优势，即利用单一模态Lamb波可准确识别损伤反射回波，且可以判断损伤反射回波模态。根据损伤反射回波传播时间，并结合对应的群速度，计算出损伤与传感器的间距，结合实际距离分析了计算结果误差。针对理论与实验群速度不一致的问题，提出了一种改进的计算方法，有效减小了由群速度差异引起的计算误差，最终将计算结果误差降低到3%以下。