基于栈式降噪自编码器故障诊断方法研究

2020-03-12赵聪杰武博翔

科技与创新 2020年4期

罗毅，赵聪杰，武博翔

（华北电力大学控制与计算机工程学院，北京102206）

在复杂工业系统中，结构复杂，单一部件发生故障时，往往难以准确地判断其发生位置，进而可能造成严重的安全事故。传统的基于神经网络的故障诊断方法[1]多为浅层神经网络，难以适应当前复杂的工业系统故障诊断需求。

深度学习作为机器学习[2]的一个新发展方向，具有强大的处理复杂数据的能力，能自动学习、提取数据隐含特征，取得了较好的效果，已经在图像识别[3]、故障诊断[4]等领域取得了快速发展。

本文通过将深度学习理论应用于复杂工业系统故障诊断中，提出栈式降噪自编码器与核主成分分析算法相结合方法构建深度学习故障诊断模型。并在此模型基础上进一步对KPCA-SDAE 模型参数进行分析研究[5]，通过对不同激活函数和优化器等参数的设置，比较模型测试数据的准确率、训练速度等结果，得出不同参数设置对KPCA-SDAE 模型的影响，找出模型的最优参数设置。

1 KPCA-SDAE 的模型设计

1.1 核主成分分析原理

通过非线性映射函数φ将原空间数据X=（x1，x2，…，xm）映射到高维空间得到特征样本数据φ（X）=[φ（x1），…，φ（xm）]，可得：

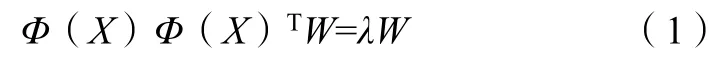
通过式（1），求得特征向量W=（w1，w2，…，wd），得到：

将式（2）带入到式（1）并左乘Φ（X）T得到：

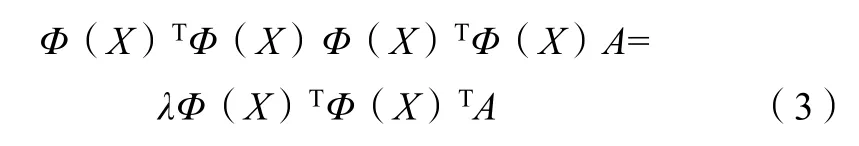
用核矩阵K 代替Φ（X）TΦ（X）得到：

通过式（4）求取高维空间下的特征值和特征向量，进而得到经过核主成分分析处理后的数据。

1.2 SDAE 网络结构

SDAE 神经网络由多层DAE 构成，将前一层DAE 的隐含层输出作为下一个DAE 的输入，通过DAE 叠加构建深度神经网络的模型。为了使SDAE 具有分类识别的功能，在SDAE 最后输出层加入了softmax 分类器，以实现系统故障的分类。

1.3 KPCA-SDAE 算法实现

本文先通过KPCA 对数据进行非线性化处理，挖掘数据非线性信息，提取故障特征，降低数据维数，将经过KPCA处理后的数据作为栈式降噪自编码器的输入数据。

栈式降噪自编码器将无监督自学习与有监督学习相结合，进行模型训练，对训练好的模型进行微调，提高模型故障诊断正确率。针对复杂工业系统故障特性，本模型为四层神经网络模型，第一层为输入层，二、三层为隐含层，第四层为分类层。

2 实验测试与分析

2.1 实验数据来源

本文选取TE（Tennessee Eastman）复杂工业系统[6]模型为实验仿真模型，对复杂工业系统进行故障诊断研究。选择TE 系统21 个故障中的6 个故障进行实验验证。这6 个故障中包含3 个阶跃故障、1 个随机故障、1 个慢漂移故障和1个执行器卡死故障，每个故障选取880 个训练数据，400 个测试数据。

2.2 测试方案

损失函数选取交叉熵函数，交叉熵函数在分类问题上具有广泛的优势，其数学表达式为：

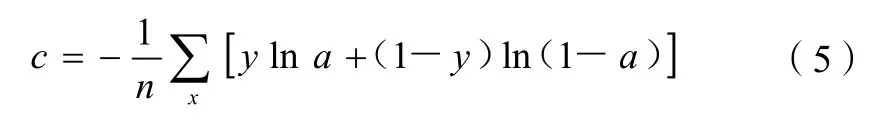
式（5）中：c 为模型的损失值；a 为预测值；y 为真实值的分类。

数据的标签选用one-hot 编码为数据标签，例如向量[1 0 0 0 0 0]表示故障1，向量[0 1 0 0 0 0]表示故障2，以此类推表示系统的故障。

2．2．1 激活函数的选择

激活函数选择不同，模型的正确率也会不同，选用Sigmoid 函数、Tanh 函数、Softplus 函数、Elus 函数以及Relu函数进行模型训练。

对于不同的激活函数，模型的训练速度和正确率会有差别，比较了不同激活函数对模型的影响。各激活函数下模型损失值比较结果如图1 所示。

图1 不同激活函数下模型损失值变化

由图1 可看出，以Relu 函数和Tanh 函数作为激活函数的的训练效果最优，损失值下降速度最快。其中，Elus 函数相比于Relu 函数和Tanh 函数虽有较好的优势，但损失值的下降速度要低于Relu 函数和Tanh 函数。Softplus 函数和Sigmoid 函数效果最差，难以寻到最优值，在本模型中具有一定的缺陷。

为了进一步验证激活函数对模型的影响，对各激活函数训练时间和正确率进行研究，具体如表1 所示。

表1 不同激活函数对模型的影响

表1 中，Softplus 函数的运行时间最长，正确率却只有91.75%，要低于其他激活函数，Relu 函数作为激活函数，运行时间是225.47 s，其正确率最高。Tanh 激活函数的正确率与Relu 函数接近，但是程序运行时间要高于Relu 函数，Sigmoid 函数的运行时间和Tanh 的运行时间相差不大，但是其正确率要低于Tanh 函数。

综合图1 损失值变化情况，Relu 激活函数在KPCASDAE 神经网络模型中具有较大的优势，选择Relu 函数作为模型激活函数。

2．2．2 优化算法的选择

优化算法代表着深度学习模型的优化方向，不断逼近最小偏差寻找模型的最优解。常用的优化器有GradientDescent算法、Momentum 算法、Adagrad 算法、Adadelta 算法、Adam算法等。

选用以上5 种优化算法对模型进行训练，比较各优化函数损失值变化，如图2 所示。

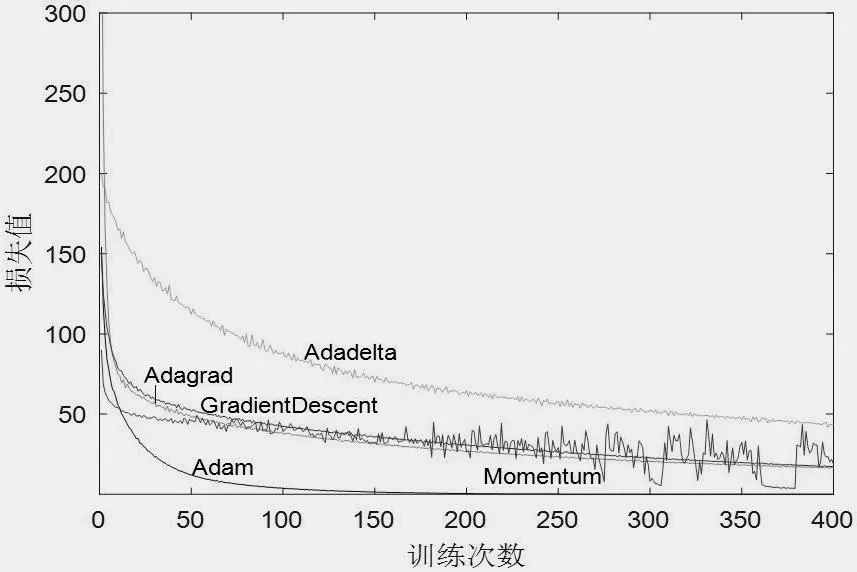
图2 不同优化算法下模型损失值变化

由图2 可以看出Adam 优化函数具有良好的寻优效果。其中，Adagrad 优化算法、GradientDescent 优化算法以及Momentum 优化算法寻优效果区别不大，比较相近，但是Momentum 优化算法在200 轮训练以后会发生波动，效果变差。Adadelta 优化算法优化效果最差，难以准确快速地寻优。为了进一步比较各个优化算法对模型的影响，对其训练时间和故障诊断正确率进行比较，如表2 所示。

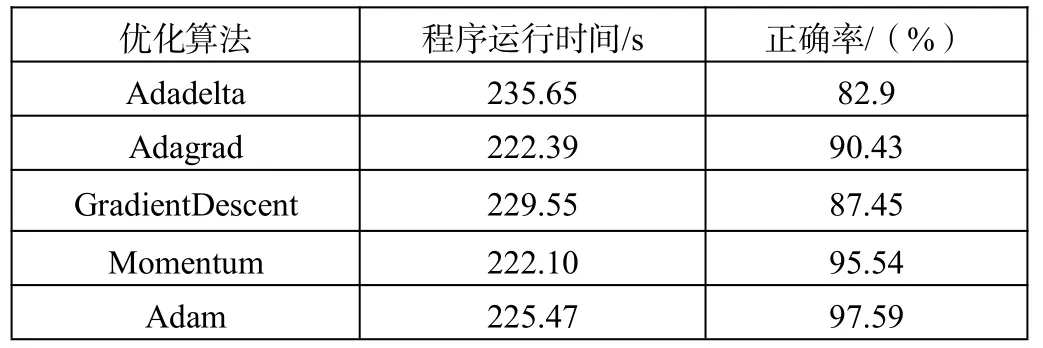
表2 不同优化算法对模型的影响

由表2 可看出，Adam 算法的正确率最高，准确性方面具有较大的优势。其中，Adagrad 算法和Momentum 运行时间都是222 s，Adagrad 算法的正确率要低于Momentum 算法，Adadelta 算法和GradientDescent 算法的正确率都在90%以下，在所选择的这5 个优化算法中具有一定的劣势，且Adadelta 算法的运行时间最长。综上所述，Adam 算法的运行时间虽然不是最短的，但其正确率要远高于其他算法，且通过图2 也可看出Adam 优化算法在本模型KPCA-SDAE 中的优化效果最好。

综上所述，Adam 算法和Relu 激活函数在KPCA-SDAE深度学习算法中能够有效地逼近最小偏差，其模型故障诊断效果最好，参数选择Adam 优化算法和Relu 激活函数，KPCA-SDAE 模型的性能最好。