原子分子光子系统的耗散相互作用和退相干

景 俊

（浙江大学物理学系光学研究所，杭州 310027）

1 引言

原子分子系统与量子化的电磁场或光子模式耦合的系统［1］无论在理论还是实验方面都是非相对论量子力学研究的主要对象和模型［2-4］.如果将系统拓展到人工原子、超导回路、离子阱、光子晶格、量子点等新量子平台［5-11］，那么它不仅涵盖了传统的原子分子物理和量子光学的主要内容，而且构成量子信息和量子调控的物理基础［12，13］.正如在单个二能级原子和单模激光场的耦合模型——Jaynes-Cummings模型中所观察到的，如果不考虑能量耗散和量子退相干效应，那么它的动力学是相干且可逆的.这正是薛定谔方程所描述的结果.

对人工原子，包括量子点、超导量子比特、里德堡原子，以及新颖电磁辐射源，包括激光、微波激射、同步辐射、微波源的广泛研究涵盖了从无线电波到远红外的频段与原子分子系统的耦合，从而在相当程度上再次引起人们对原子与光相互作用的兴趣.新的研究方法能够获得有关原子和分子结构以及动力学的更确切的信息、从而有助于控制原子和分子的内部和外部自由度、并且产生新的辐射形式.这些进展已经引来越来越多的物理学家、化学家、其他研究人员和工程师对物质和低能辐射之间发生的作用［14-17］产生兴趣.

本文的目标是为已经具有一定量子力学和原子分子物理基础的研究人员介绍在开放量子力学框架下研究原子与光相互作用的基础理论，特别是关于量子系统退相干动力学的描述理论——主方程.主方程及其等价方法构成了整合涉及物质―辐射相互作用的几乎所有物理方面的基本工具［18-23］.

2 开放量子系统与量子退相干

在量子力学基本问题方面，含时薛定谔方程以及冯诺伊曼方程已经在原则上提供了闭合量子系统的动力学方程.如果不计较开放系统的环境或者噪声对它的影响和作用，或者拥有对全部希尔伯特空间的计算能力，就没有必要在开放量子系统的框架下处理问题.但实际上对于大多数实际问题这两者都是无法做到的.

首先定义何为环境.在全量子框架下，环境是与量子系统相互作用的另一个量子系统，拥有足够多、足够复杂的自由度，以至于相对人们感兴趣的量子系统而言，是不受控制的.具有可操作性的处理方案的前提是通过测量或物理建模给出环境自由度的统计性质.这些性质包括且不限于玻色统计或费米统计、谱密度函数、关联函数、温度——如果它处在热力学平衡态下的话.然后通过理论推演，使得这些统计性质反映在受研究的量子系统的动力学方程中.

其次何为噪声.布朗运动中的涨落可以当作是一种经典噪声，按照涨落—耗散定理的要求，它具有一定的关联函数和谱密度函数，它们两者互为傅里叶变换关系.量子系统面对的噪声，可以是经典噪声，也可以是量子噪声.在物理上，两者都要符合涨落—耗散定理；在特定情况下，符合一定关联函数的经典噪声和量子噪声对系统的影响在系综统计后不可区分.因此有时可以用噪声取代环境自由度的全量子化处理.在纯量子框架下，噪声可以直接用环境算符以及耦合系数直接表达出来.就其效应而言，有时需要特别指出，哪些噪声造成了系统的退极化和能量耗散，哪些噪声不涉及能量损耗而直接反映出同一系综内不同量子系统在相位上的脱散.前者反映了原子分子系统的布居数在高低能态上的转移；后者代表了相位关联的消失.对量子系统而言，前者当然也同时引起系统间失去相位上的固有联系，但后者在许多文献中才被称为“纯量子的退相干”.

因此量子退相干本质上是一种量子力学效应，与经典耗散或随机涨落有所区别，虽然后者也会引起量子效应.在哥本哈根学派定义的量子测量假设以及后来由冯诺伊曼严格化后的量子测量理论中，不难发现退相干是量子测量的效应.测量仪器扮演了量子化的环境自由度的角色，系统根据与待测物理量配套的测量仪器指针态展开的本征基矢做随机投影.无论是读出结果的测量，还是不读结果的测量，指针态对应的本征基矢之间的相干项在测量后全部消失了.在广泛关注量子信息处理的前沿研究中，退相干显然是任何量子处理，特别是量子计算，或任何必须利用量子线性叠加原理优势的技术不可回避的问题.它在绝大多数时候显然是难以逾越的障碍.根据DiVincenzo为可行的量子计算机定出的必须满足的若干条件，量子系统的相干时间除以量子门的运行时间必须足够大，否则量子线路模型就没有实际价值.所以无论是量子物理的基本问题，还是量子前沿技术的发展，都需要人们重视退相干过程的基础研究，从而设计出提高量子相干时间的方案，或者要么回避、要么正面利用退相干效应.这里不对此做展开.

3 主方程的推导方法

现在进入技术性环节——如何建立开放的原子分子系统的退相干动力学主方程.“主”这个词意思就是关注某一少自由度或少体系统，而把其环境或不关心的希尔伯特子空间对该系统的作用考虑到方程的结构和参量中去，最后得到方程仅含有少自由度或少体系统的算符.假设初始时刻系统与环境是没有耦合的，即ρT（0）=ρS（0）⊗ρE（0），且整体哈密顿量可写为：

其中HS是系统的自由哈密顿量，HE是环境的自由哈密顿量，HI=∑iSi⊗Ei是系统与环境相互作用哈密顿量，这里的Si和Ei分别表示系统和环境的算符，Si代表第i种量子退相干通道.α用来衡量相互作用哈密顿量相对系统自由哈密顿量的相对幅度，一般符合微扰论的要求.为简单起见，以下在相互作用表象下进行推导，即对所有算符O，都有

首先从整体系统的冯诺伊曼方程出发（它总是成立的）：

然后对该方程做第一步马尔可夫近似以及玻恩近似，即将（4）式的ρT（s）替换为ρT（t），物理上抛弃了从初始时刻到当下时刻之前的系统演化历史对系统当前变化量的贡献，而是只关心当下时刻的贡献，数学上带来的误差为O（α3）.并让方程等号两边都对环境部分自由度进行部分求迹，从而得到关于系统密度算符的二阶微扰的动力学方程（注意在下面这个方程后，不再使用约等号）：

其中第一项正比于TrE［Ei（t）ρE（0）］，也就是环境算符Ei的期望值，可以将其设为零.这本质上不是一个假设，因为总可以令HI→∑iSi⊗（Ei-〈Ei〉）、HS→HS+α∑i〈Ei〉Si.在环境弛豫时间远小于系统动力学时间的假设下，可以认为环境状态基本不变（一般可认为环境处在热力学平衡态），这就得到了微扰论下的玻恩-马尔可夫主方程（Born-Markov master equation）：

它在二阶微扰成立的前提下可以包含量子环境的结构参量，也就是各模式与系统的相对耦合强度、各模式自身的本征频率的统计信息，因而在许多文献中也被称为“非马尔可夫”主方程.注意它不是“精确主方程”［23］，因为没有包含结构化的环境对系统动力学的所有阶次的贡献.从微扰论物理的角度需要进一步明确两点：1，主方程的建立基于系统-环境相互作用哈密顿量与系统自由哈密顿量之间存在能量/时间的尺度分离，否则对全部希尔伯特空间的计算就不可避免了.2，环境的状态一般默认为热力学平衡态，那么系统在环境噪声下的随机量子跃迁过程和耗散应该受到涨落-耗散定理的限制.

4 真空环境下的Lindblad主方程

以下用相对具体的一个例子进一步推演，为简单起见，将α吸收进方程.假设相互作用哈密顿量HI=S B†+S†B.系统跳跃算符满足S（t）≡eiHStS e-iHSt=S e-iω0t，其中ω0是原子分子系统本征频率.环境自由哈密顿量为环境集体湮灭算符为B=∑kgkak.这里ak是玻色环境的湮灭算符，gk是耦合系统与第k个模式的耦合系数.所以在相互作用表象下，

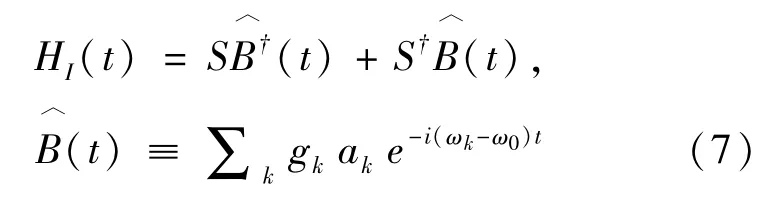
于是玻恩-马尔可夫主方程可具体表达为

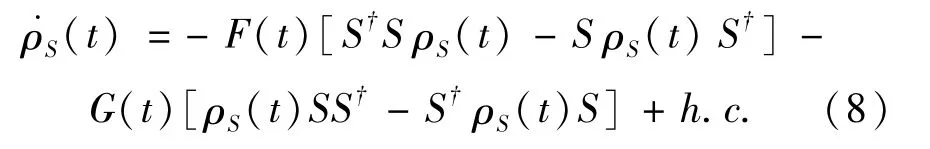
其中两个含时系数的定义是

这里暗含环境状态ρB为热力学平衡态的假设.另外对于许多本征频率为微波波段的人工原子而言，光频波段的电磁环境因为能量与之远不匹配而总可以认为处在真空或零温.所以可合理假定电磁环境处在真空态或零温，则有

其中J（ω）=∑k|gk|2δ（ω-ωk）是环境态密度或模式密度函数.而G（t）=0.略加计算，即将F（t）的积分上限推至无穷，消除其含时特征，也就是执行第二步马尔可夫近似，就可以得到相互作用表象下的Lindblad型主方程：

5 讨论

需要再次强调的是，主方程是量子力学框架下的动力学方程——不难发现它在幺正变换下保持形式不变.一个合理的主方程必然得到合法的系统密度矩阵，也就是每一时刻的系统密度矩阵必然是半正定的.动力学方程所对应的系统状态的映射必须是全正定且迹守恒（Complete Positive Trace-preserving）.要得到特定物理体系的主方程，原则上应从特定全量子模型出发，仿照前文步步推演，不可以做过分的非物理的近似.比如将玻恩-马尔可夫主方程的积分上限推至无穷有时候在短时动力学中会带来非正定的问题，其物理原因就是这种近似违背了物理定律的因果律.以Lindblad方程为代表的现象学方程，比如量子光学领域熟悉的光学布洛赫方程，只要保证系数为正常数，就不会带来非物理的结果.但是它不能反映强耦合情况下的物理，比如非马尔可夫效应.另外跳跃算符应用系统哈密顿算符的本征态基矢展开，从而在物理上对应真实的量子跳跃（quantum jump）过程.只有本征态基矢之间的瞬时量子跳跃才能正确地描述微观量子过程.

值得指出的是，只有极其少数特定主方程可以得到解析解.比如纯退相位（pure dephasing）模型和零温环境下的少数量子跳跃模型.有时不得不采用量子跳跃方法（quantum jump method）、量子轨迹方法（quantum trajectory approach）或量子郎之万方程替代量子Lindblad 方程进行数值求解.比如可以证明：以下的量子态扩散方程（一种量子轨迹方程或随机薛定谔方程）［24，25］与Lindblad方程完全等价：

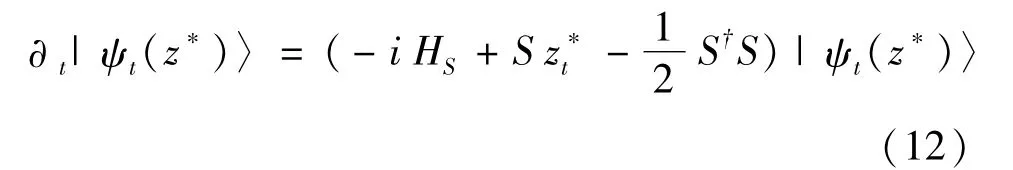
其中z*是满足系综平均条件的高斯型白噪声，这里M［·］是指对系综求平均值.求解随机薛定谔方程后还要对噪声轨迹求系综平均，从而得到密度矩阵ρS（t）=M［|ψt（z*）〉〈ψt（z*）|］.

6 总结和展望

量子退相干理论在当前研究中的兴起和应用伴随着单量子系统的实验实现.通常布洛赫方程或者爱因斯坦几率方程被用来描述受到电磁场驱动的原子分子系综的动力学.但离子阱、单模腔、量子点、超导回路等新兴量子平台的发明提供了观察和操控单个粒子的可能性.对辐射场信息的获取，比如通过对系统发射到环境内光子的探测，会导致系统波函数的突变.无论是探测到光子还是没有探测到，也就是零结果，都会导致信息的增加.这样新的洞察便会注入到原子光子动力学及耗散过程中，这就发展出新的退相干动力学方法.除了对物理的新洞察，这些方法也会使得对复杂问题的模拟成为可能，比如用主方程方法也可处理激光冷却问题.