两区域互联电网的神经元变结构PID频率控制

魏 萌，周晓华

(广西科技大学 电气与信息工程学院，广西 柳州 545616)

0 引言

自动发电控制(Automatic Generation Control，AGC)是电力系统发电量控制的一种情形，是实现频率二次调整的控制方式。当系统负荷在10 s～3 min的周期内出现幅值较大变化时，需要由电力系统控制中心根据系统频率和互联系统联络线功率的偏移程度，起动AGC以实现系统负荷频率的控制。AGC可分为经济频率调度(Economic Dispatching Control，EDC)和负荷频率控制(Load Frequency Control，LFC)两种功能，其中，LFC根据区域控制偏差(Area Control Error，ACE)在线调整发电机组的有功出力，是一种适应负荷波动的反馈控制。

为改善传统LFC系统控制性能，已有很多学者进行了研究并取得了大量研究成果。文献[1]采用模型预测控制CMPC对两区域互联电网AGC系统控制进行了研究，强化了两区域互联电网的动态性能，增强了其鲁棒性。文献[2]采用灰狼优化算法加快了PI/PID控制器的参数优化与整定，改善了AGC系统的动态响应性能。文献[3]采用PSO-GSA对PID控制器参数进行优化，并与PSO算法和GSA算法相比较，有效增强了两区域互联电网AGC系统的鲁棒性。文献[4]在考虑对控制器参数、系统参数优化的同时，寻找求解二者之间的数学关系，并建立了基于尼克尔斯(NICHOLS)曲线PID控制的互联水电系统负荷频率控制LFC模型，增强了系统的抗干扰能力。文献[5]采用改进的粒子群PSO智能算法对PI控制器参数进行优化，并将其应用于风电互联系统的频率控制，较好地解决了系统风电并网时发生的频率波动问题，同时优化了两区域互联电网的性能指标。文献[6]采用社会学习自适应细菌觅食(SLABFA)算法优化传统PI控制器参数，提高了算法的寻优精度和收敛速度，然后将其应用于两区域互联电网AGC系统控制中，获得了较好的控制效果。

神经元变结构PID控制算法[7]对控制对象模型的精度要求低，其原理简单、程序易于编写，对非线性系统具有相对较强的控制能力。本文将神经元变结构PID控制算法应用于两区域互联电网AGC系统的控制中，采用MATLAB/Simulink 仿真平台搭建两区域互联电网AGC 系统仿真模型，然后对所提控制方法进行仿真验证，仿真结果验证了所提方法的有效性。

1 神经元变结构PID控制原理

神经元变结构PID控制原理[8]如图1所示，通过转换器计算，可得到神经元1的三个输入状态x11(k)，x12(k)和x13(k)分别为:

(1)

式中，r(k)为给定信号；e(k),e(k-1)为k和k-1时刻的误差信号；y(k)为控制对象在k时刻的实际输出信号。

神经元1利用权值的在线调整功能实现变结构PID控制器的三个参数Kp，Kd和Ki在线调整，具体的调整算法如下：

(2)

式中，K1，K2，K3为神经元1的输出比例增益；w11(k),w12(k)，w13(k)为神经元1在k时刻的权值。

神经元1权值w11(k)，w12(k)，w13(k)的调整算法如下：

(3)

式中，η11，η12，η13为神经元1的学习速率；w11(k-1)，w12(k-1)，w13(k-1)为神经元1在k-1时刻的权值。

神经元2的输入状态x21(k)，x22(k)分别为：

(4)

设β(k)为微分环节调节系数，[1-β(k)]为积分环节调节系数，当误差绝对值小于阈值ε时，β(k)=0；当误差绝对值大于等于阈值ε时，β(k)的值随神经元2的权值的变化在线调整，其计算方法如下:

(5)

式中，w21(k)，w22(k)为神经元2在k时刻的权值。

与神经元1类似，神经元2权值w21(k)，w22(k)的调整公式为：

(6)

式中，η21，η22为神经元2的学习速率。

此时，神经元2输出的控制量为：

u(k)=u(k-1)+β(k)·K·Kd(k)[e(k)-e(k-1)]+[1-β(k)]·K·

Ki(k)[e(k)-2e(k-1)+e(k-2)] .

(7)

式中，K为神经元2的输出比例增益。

由式(7)可知，当误差e(k)较大时，通过在线调节β(k)，可实现积分环节与微分环节权重的调控，而当e(k)较小时，仅有积分环节发挥作用，实现了变结构功能。

将神经元2输出的控制量加上比例控制环节后，即可实现神经元变结构PID控制，其控制量为：

u(k)=u(k-1)+Kp(k)e(k)+β(k)·K·Kd(k)[e(k)-e(k-1)]+[1-β(k)]·K·

Ki(k) [e(k)-2e(k-1)+e(k-2)] .

(8)

2 两区域互联电网频率控制系统建模

自动发电控制AGC是互联电力体系管控的基本内容[9]。AGC是一种计算机闭环反馈控制，能够准确控制系统在3 min内的功率不平衡问题。AGC系统相当于追踪调控系统，以实现机组经济有效的运行。AGC主要实现电力系统对发电量的控制，通常称为频率的二次调整。当一次调频已进行完毕，但频率偏差超出预期标准时，则需要进行频率的二次调整。这种由非发电机组的计算机控制实现的电力系统自动发电量控制可分为负荷分配器和发电机组控制器两大部分。其中，负荷分配器是根据电力系统的频率以及相关测量信号，依据相关控制准则来明确各个发电机组的最优设定输出功率；根据负荷分配器给予各发电机组的最优设定输出功率，发电机组控制器调整控制调速器的调节特性，获得在额定频率下与设定最优输出功率相等的实际输出功率。AGC通过小型计算机控制调节各发电机组的出力，消除由多区域频率偏差、联络线功率偏差等造成的区域控制偏差ACE(Area Control Error，ACE)，其目标是尽可能将每个区域控制偏差δACE调节整定到零。

对于两区域互联电网，控制偏差ACE的表达式可写为:

(9)

式中，φ1,φ2分别是两个区域的频率偏差因子；Δf1，Δf2分别是两个区域的频率偏差；ΔG1，ΔG2分别是两个区域的发电功率变化量；ΔPL1，ΔPL2分别是两个区域的有功负荷变化量；ΔP为两个区域间联络线功率偏差变化量。δACE1为区域一的控制偏差，δACE2为区域二的控制偏差。

联络线功率的值规定以目标区域输出的联络线功率方向为正方向，以目标区域输入的联络线为负方向。频率偏差因子φ表示频率扰动时相连区域相互作用的比重，计算公式如下：

(10)

式中，R为发电机调差系数，D为负荷调节效应(由于D对频率偏差因子的影响效果很小，本文假定D=0)，φ是频率变化1%的功率变化百分数。

当两区域互联电网系统达到稳态时，Δf1=Δf2=0，ΔP=0。为确保AGC系统始终处于调节状态，积分增益应取足够小的数。

为充分利用PID控制的稳定性能，本文将PID控制作为主控制，神经元变结构PID控制作为辅助控制的控制结构[10]，对LFC的控制器进行了设计。PID1参数为Kp1=12.2，Kd1=1.78，Ki1=2；PID2参数为Kp2=4.8，Kd2=1.32，Ki2=0.61。神经元变结构PID控制器采用S函数编程实现，为简化控制器参数的调整过程，两个神经元变结构PID控制器的参数设置相同，其参数设置如下：神经元1比例增益分别为K11=0.98，K12=0.01，K13=0.001,初始权值w11(0)=w12(0)=w13(0)=0.5,学习速率η11=100，η12=60，η13=50；神经元2比例增益为K=90，初始权值为w21(0)=w22(0)=0.5，学习速率η21=100，η22=100，阈值ε=0.01。

在MATLAB/Simulink仿真平台建立的两区域互联电网AGC控制系统模型如图2所示。AGC频率控制系统为两区域再热式火电互联系统，主要由负荷、发电机、调速器、再热式火电机组组成。图中，Δf为区域的频率偏差，Tp为发电机时间常数，Kp为发电机惯性常数，T12为两区域间联络线同步系数，ΔPL1为第一个区域的阶跃扰动负荷，ΔPL2为第二个区域的阶跃扰动负荷，K1为汽轮机再热系数，T2为汽轮机再热时间常数，Kt为汽轮机惯性常数，T1为汽轮机时间常数，Kg为调速器惯性常数，Tg为调速器时间常数，R1为第一区域调差系数，R2为第二个区域调差系数，φ1为第一区域的频率偏差因子，φ2为第二个区域的频率偏差因子。

AGC主要有定交换功率控制(Flat Tie-line Control，FTC)、定频率控制(Flat Frequency Control，FFC)、联络线功率及频率偏差控制(Tie-line load frequency Bias Control，TBC) 三种控制模式。其中，TBC控制模式可以同时接收频率偏差分量与联络线功率偏差分量，是互联电力系统常采用的控制模式[11]。当系统开始扰动时，电力系统频率与联络线功率会发生一定的偏移量，从而产生ACE，AGC开始运行，使ΔP与Δf为零。两区域互联系统参数如表1所示。

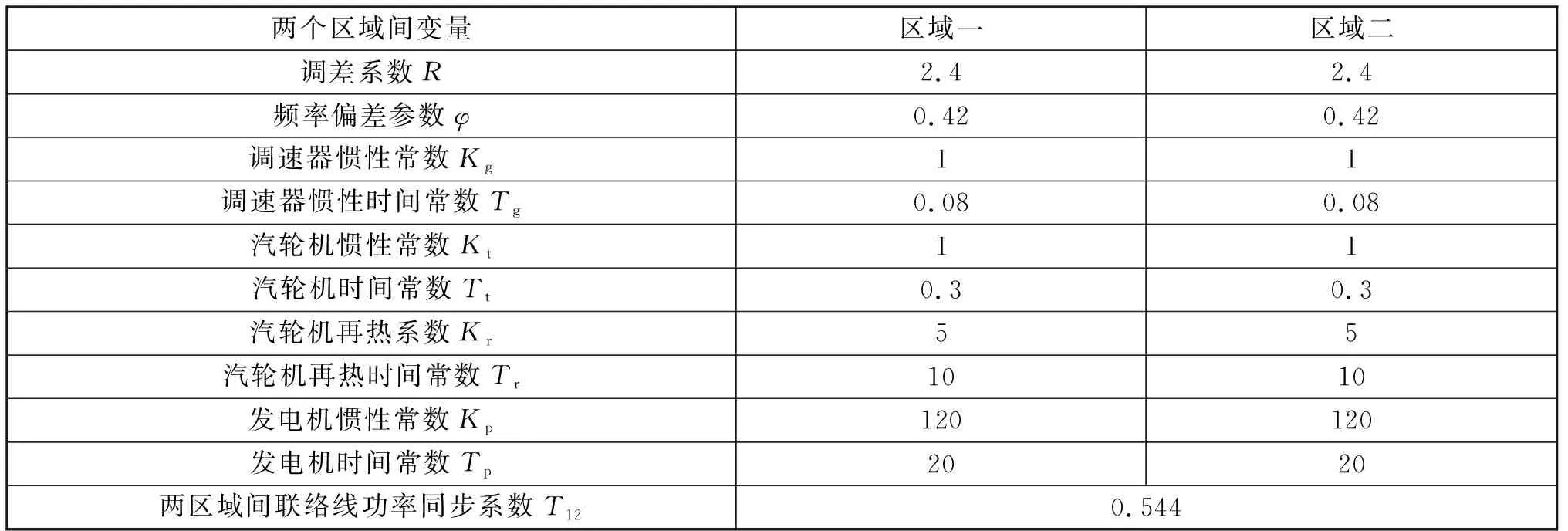
表1 两区域互联系统参数

3 仿真研究

仿真情形一：当两区域有功负荷功率变化量ΔPL1=ΔPL2=0.1 p.u.时，仿真波形如图3所示。

从图3(a)可以看出，本文控制方法在14 s后频率偏差达到零的状态，且频率偏差超调量小，而传统PID控制的稳定时间为22 s，本文控制方法的响应速度明显快于传统PID控制。观察图3(b)，本文控制方法区域二频率偏差在12 s后频率偏差达到零的状态，且频率偏差超调量小，而传统PID控制的稳定时间为20 s，本文控制方法的响应速度明显快于传统PID控制。从图3(c)可以看出，本文控制方法的联络线功率偏差在20 s时已下降至0，而传统的PID控制在30 s时联络线功率偏差才下降至0。此仿真情形中，两区域有功负荷增加，系统频率降低，经控制器调节后频率偏差下降至0，系统频率恢复到稳定值，区域联络线功率从区域一流向区域二。

神经元变结构PID控制器的比例系数Kp、微分系数Kd及积分系数Ki的变化曲线如图4(a)—图4(c)所示。

仿真情形二：当两区域有功负荷功率变化量为ΔPL1=0.1 p.u.，ΔPL2=0.2 p.u.时，仿真波形如图5所示。

由图5(a)可知，本文控制方法区域一频率偏差在18 s后频率偏差达到零的状态，且频率偏差超调量小，而传统PID控制的稳定时间为22 s，本文控制方法的响应速度明显快于传统PID控制。观察图5(b)，本文控制方法区域二频率偏差在12 s后频率偏差达到零的状态，且频率偏差超调量小，而传统PID控制的稳定时间为20 s，本文控制方法的响应速度明显快于传统PID控制。由图5 (c)可知，本文控制方法具有较强的自适应能力，在18 s时功率偏差已达到0。

神经元变结构PID控制器的比例系数Kp、微分系数Kd及积分系数Ki的变化曲线如图6(a)—图6(c)所示。

仿真情形三：两区域有功负荷功率变化量为ΔPL1=0.2 p.u.，ΔPL2=0.1 p.u.时，仿真波形如图7所示。

由图7(a)可知，本文控制方法区域一频率偏差在11 s后达到零的状态，且频率偏差超调量小，而传统PID控制的稳定时间为20 s，本文控制方法的响应速度明显快于传统PID控制。观察图7(b)，本文控制方法区域二频率偏差在16 s后达到零状态，且频率偏差超调量小，而传统PID控制的稳定时间为22 s。本文控制方法的响应速度明显快于传统PID控制。由图7(c)可知，25 s后本文控制方法基本达到无联络线功率偏差状态，而PID控制则在30 s后才能达到无联络线功率偏差状态。

神经元变结构PID控制器的比例系数Kp、微分系数Kd及积分系数Ki的变化曲线如图8(a)—图8(c)所示。

4 结论

神经元变结构PID控制器设计灵活性较强，可应用于非线性系统。本文提出了一种两区域互联电网神经元变结构PID的频率控制方法，采用传统PID控制为主控制、神经元变结构PID控制为辅助控制的控制方案，神经元变结构PID控制用一个神经元实现变结构PID控制，同时用另一个神经元在线调整PID控制参数。仿真结果表明，在相同的仿真时间和参数设置下，与传统PID控制相比，本文所提出的控制方法的控制效果更佳，控制器结构简单且算法易实现。将其用于互联电网的频率控制能够缩短调节时间，可更快达到有功功率平衡状态，能有效降低频率偏差，快速使互联电网的频率达到额定值状态。通过在线调整神经元PID控制器参数，能增强控制器的自适应能力，可有效缓解两区域互联电网频率波动问题。