壁湍流等动量区对惯性颗粒分布的影响
2020-03-11姚易辰许春晓
姚易辰, 许春晓
(清华大学 工程力学系, 北京 100084)
0 引 言
含颗粒壁湍流是自然界和工程中广泛存在的流动现象。由于湍流具有多尺度性、不规则性和强非线性等特点,使得关于湍流本身尚存在诸多难题,而颗粒相的加入,使得问题变得更加复杂。在壁湍流中,人们已经发现存在所谓的拟序结构或称相干结构,它们出现的位置和时刻具有随机性,但一经出现,就以特定的规律进行演化,在湍流的发生、发展和输运中起关键作用,当然也对壁湍流中颗粒的输运特性和聚集行为产生重要影响。因此从相干结构的角度研究颗粒的运动规律,对理解颗粒的分布特性及其内在机制具有重要意义。
在壁湍流中,根据离开壁面距离的不同,可将壁湍流分为黏性壁区和外区,黏性壁区包括了黏性底层、缓冲区和部分对数区,在不同的区域,存在不同尺度的相干结构。速度条带与流向涡是近壁区典型的相干结构[1],它们以黏性尺度标度,流向涡的抬升机制产生条带,条带失稳破碎产生流向涡,这样一个准周期的自维持过程是壁湍流产生和维持的重要机制[2]。近年来,人们有能力对更高雷诺数的壁湍流开展研究,发现在对数区和外区还存在所谓的大尺度运动、超大尺度运动以及等动量区等流动结构。等动量区是由Meinhart和Adrian在湍流边界层实验中首先观察到的[3],他们发现在整个边界层厚度范围内,存在着一系列瞬时流向速度近似相等的区域,他们将其称之为等动量区(Uniform Momentum Zone,UMZ)。等动量区的特征模态速度可以通过流向速度的概率密度分布获得[4-5]。不同等动量区之间的交界面上,存在较薄的强剪切层并包含一系列展向涡结构。等动量区的流向尺度可以达到数倍边界层厚度[4],并且大尺度等动量区沿着流向的排列与发卡涡包内层级状的涡结构排布存在密切联系[6]。Lee和Sung[7]通过对直接数值模拟数据的分析,发现发卡涡群在流向有序排列,产生了沿流向拉长的高低动量区。在等动量区之间的界面处,速度变化剧烈,存在高剪切,产生了大量的顺转(与平均剪切同向)展向涡[8]。基于流向速度的概率分布,Kwon等[9]在槽道湍流中将等动量核心区进行了识别,发现0.95倍的中心线速度可作为区分核心区和非核心区的速度阈值。
关于湍流场中颗粒聚集形态的研究,传统理论认为湍流对于颗粒施加了与标量场类似的随机力,并对颗粒的空间分布起扩散作用,因而颗粒在湍流场中的分布会趋向于全场均匀。然而颗粒与标量不同,颗粒具有惯性,颗粒受力并非随机的[10],并且颗粒会在湍流相干结构的作用下呈现非均匀的倾向性分布。对于颗粒在壁湍流中的分布规律,已有的实验研究[11]和数值模拟[12-13]均主要关注近壁区,并发现颗粒会在低速条带区域聚集。Maxey[14]通过渐进分析的方法发现,颗粒会在湍流场高剪切低涡量处聚集。这一现象也在含颗粒的各向同性湍流直接数值模拟中得到了验证[15],并且颗粒局部最大浓度能够达到约30倍平均浓度。关于颗粒聚集性与其特征弛豫时间的关系,Wang和Maxey[16]发现当颗粒弛豫时间与 Kolmogorov时间接近时,颗粒的倾向性聚集程度最为明显。尺度较大的颗粒由于其弛豫时间较长,仅仅对大尺度湍流涡结构的作用存在较强响应。而尺度较小的颗粒能够快速跟随流体质点的运动轨迹,颗粒间距受流体不可压条件限制很难达到局部极高浓度[17]。同时颗粒浓度与流场拓扑结构的研究表明,颗粒倾向于聚集在相邻涡结构之间剪切主导的鞍点区。关于颗粒聚集性的雷诺数效应,Wang等人[18]发现在各向同性湍流中,颗粒的聚集程度与雷诺数呈现单调递增关系,由于流场涡结构的间歇性随着雷诺数增强,进而颗粒聚集性也随之增强。对于含颗粒槽道湍流,由于颗粒场平均浓度沿法向的非均匀分布,因而上述规律在近壁面附近有所差异。关于槽道湍流中颗粒倾向性分布的雷诺数效应,Reade和Collins[19]的研究发现,随着雷诺数升高颗粒倾向性聚集的程度有所提高,并且随后会趋于定值。最近,Jie等[20]首次研究了摩擦雷诺数为1000的槽道湍流中非球形颗粒的旋转和取向,发现在近壁区雷诺数对颗粒的旋转和取向影响较弱,而在湍流核心区颗粒旋转受到极大的抑制。
以往对含颗粒壁湍流的研究,主要是集中在低雷诺数范畴(摩擦雷诺数~102),主要关注的是近壁区条带和流向涡对颗粒分布的影响,对于高雷诺数时大尺度运动特别等动量区对颗粒运动影响的研究还很缺乏,而自然界和工程中的颗粒两相流大多是高雷诺数湍流流动,如大气边界层对沙尘的输运等。在高雷诺数情况下,大尺度运动对湍流的贡献占主导地位,对颗粒的运动和分布也将具有重要影响。等动量区是湍流大尺度运动的一种表现形式,因此,本文对摩擦雷诺数为1000的含颗粒槽道湍流开展直接数值模拟研究,提取等动量区,并对其中的颗粒运动特性和分布规律加以研究,可以获得高雷诺数壁湍流大尺度运动对颗粒分布影响的新认识。
1 数值方法
本文以沙尘暴时粉尘的输运为研究背景,以此确定特征参数和计算方法。悬浮粉尘平均粒径约为2.5 μm,且最大粒径小于10 μm[21-22],大气边界层的Kolmogorov尺度约为1 mm[23],颗粒相与流体相的空间尺度比值小于0.01。在颗粒浓度方面,离地10 m处的场地测量结果表明,单位体积粉尘质量一般小于5 mg/m3, 对应的体积浓度小于2×10-9[24-25]。虽然粉尘颗粒的体积浓度较小,但考虑到较小颗粒粒径,每立方米的颗粒数大约在千万到10亿量级。同时对于此类悬浮粉尘颗粒,重力作用相对于Stokes力为小量。
根据体积浓度的不同,颗粒两相流的数值模拟可采用单向、双向和四向耦合方法,根据颗粒的相对大小,又可分为拉格朗日法和欧拉法[26]。拉格朗日法适用的颗粒尺度和类型更加宽泛,但其计算量与颗粒数量成正比,受计算条件限制较大。欧拉法的优势在于颗粒相的计算量与颗粒参数无关,因而特别适用于颗粒粒径较小、单位体积内颗粒数众多的问题。因此,针对尘暴问题的特点,本文采用不考虑颗粒间碰撞的平衡欧拉法来模拟颗粒两相流问题。
对于微小颗粒,Ferry和Balachandar[27]进一步提出了快速平衡欧拉法,将描述颗粒速度的微分方程关于颗粒响应时间进行展开,得到了只依赖于流体的局部速度及其导数的代数表达式。本文采用该方法对含颗粒槽道湍流进行直接数值模拟。流体和颗粒运动的控制方程如下:

(1)
(2)

(3)

(4)
其中u,a,p和ν为流体相的速度、加速度、压强和运动黏性系数;up,c和τp为颗粒相的速度、体积浓度和响应时间。ρ为颗粒与流体的密度比,β=3/(2ρ+1)为密度参数。在本研究中,我们对up采用一阶近似展开,因此根据式(4),颗粒速度只与局部的流体速度和加速度有关。在流向和展向,采用周期边界条件,在壁面采用无滑移条件。
对于流体相的控制方程(1)和(2),在流向和展向采用Fourier-Galerkin 法进行离散,在壁面法向,采用6阶紧致差分格式进行离散,采用3阶精度的时间分裂法进行时间积分[28]。对于颗粒浓度场,连续方程(3)采用2阶迎风格式进行空间离散、4阶Runge-Kutta 法进行时间推进。

为验证本文的方法和程序,首先对Reτ=150、St=1的槽道湍流进行了直接数值模拟,与文献结果对比了平均速度、平均浓度、速度脉动和浓度脉动二阶统计量的分布,均与文献结果相符,验证了程序的正确性,在此不再赘述。
2 结果与讨论
2.1 基本统计量

2.2 模态速度的提取
由等动量区的定义可知,每个等动量区内包含的流体,其流向速度分布基本相同,而不同等动量区之间的流体动量存在差异。通过流向速度的概率分布,能够划分出一系列速度接近的小区间[4],从而获得与瞬时场中速度阶梯状分布一致的等动量区模态速度。考虑到每个等动量区模态速度描述了一定空间范围内流体的整体速度特性,且各模态之间会存在一定程度的概率重叠区域。本文采用多个高斯函数叠加的形式拟合整体的速度概率分布,并将高斯函数的中心位置定义为模态速度。单个模态内速度的高斯概率分布,能够保证同一个等动量区内速度分布基本一致且体现了较多的流动事件整体上的速度特性。


(a) 平均流向速度 U+
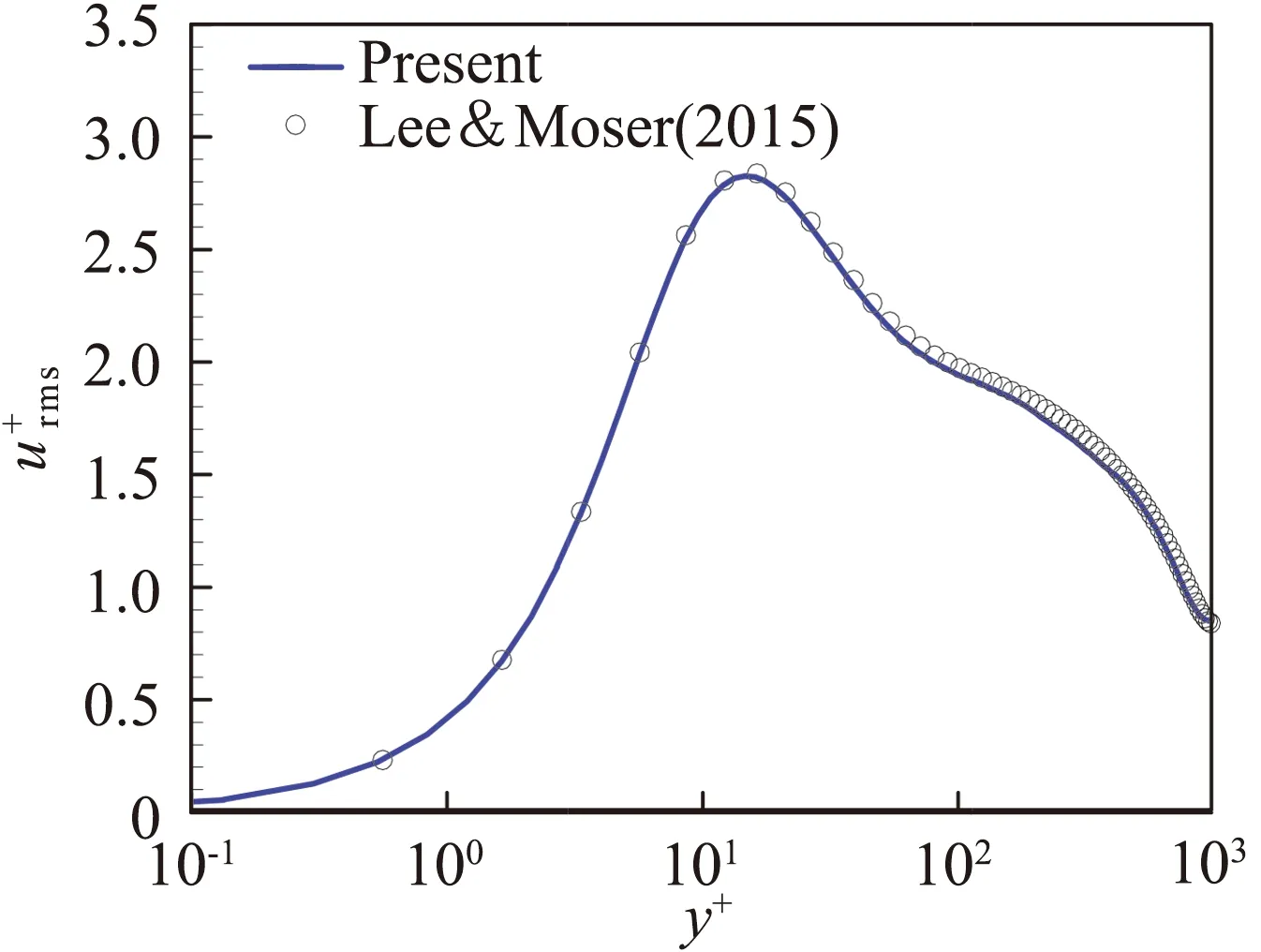
(b) 流向速度脉动均方根

(c) 平均浓度C
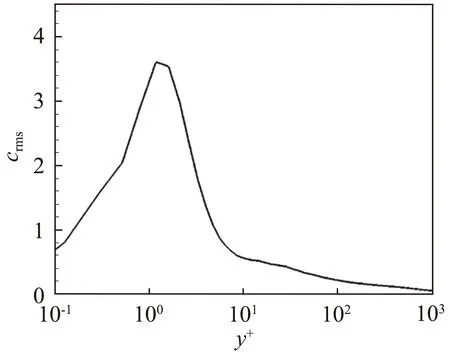
(d) 浓度脉动均方根crms
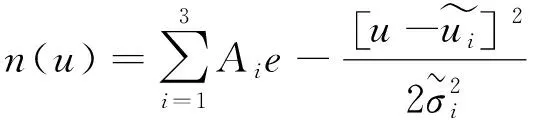
(5)
拟合的统计区域流向长度为半槽宽H[9],与发卡涡包结构的流向特征尺度一致。在模态提取的过程中,模态速度采用随机数初始化,然后采用梯度下降法更新,其目标函数选定为概率的均方差,从而使得通过高斯函数叠加形式获得的概率分布n(u)与真实的速度概率分布N(u)相符。图2显示了流向速度的概率分布以及采用3个高斯函数叠加得到的拟合曲线,该曲线与真实的概率分布可以很好地贴合。采用这种高斯函数叠加的等动量区提取方式,能够保证同一个等动量区内模态速度一致,而不同等动量区模态速度存在差异的基本要求。而常用的选取概率分布局部极大值点的模态速度提取方式,存在模态提取对概率区间划分宽度敏感、对于多重模态重叠区域判别困难等问题。而本文采用的高斯函数的模态获取方法,概率区间划分对于拟合函数结果基本无影响,同时能避免由于样本数量导致的伪特征模态的捕获。
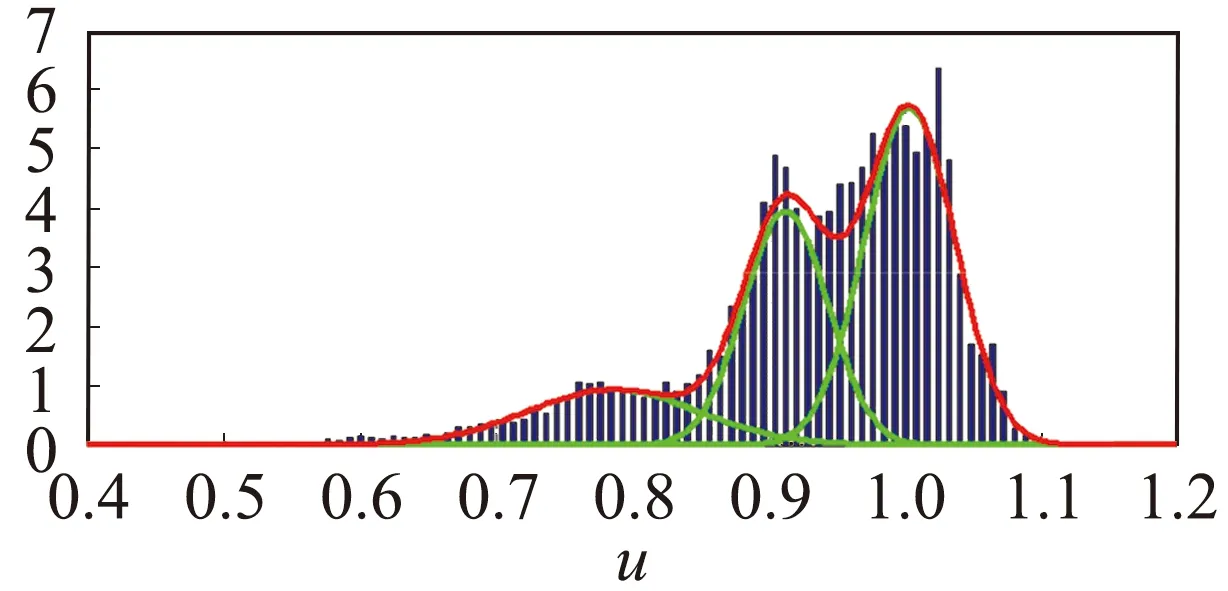
图2 流向速度概率分布和高斯函数拟合曲线蓝柱:速度概率;绿线:3个独立的高斯函数;红线:3个高斯函数的叠加。Fig.2 Probability distribution of streamwise velocity and Gaussian fitting functionThe blue column is velocity probabitity, the green curve is three separate Gaussian functions, and the red envelope is the superposition of the three functions
采用上述的模态提取方式,对于每个样本在xy平面上的瞬时速度依次提取三个特征模态速度。为方便后续讨论,按照模态速度从小到大的排列顺序,将三个等动量区依次命名为I区、II区和III区。图3为模态速度的概率密度分布图,每个区间内模态速度的概率分布关于其中心位置基本对称,且大致符合高斯分布。图中蓝色区域(III区)的平均速度约为槽道中心处平均速度(UCL),这一区域通常被称为核心区。绿色区域(II区)反映了存在于较高位置处的发卡涡包特性,其平均模态速度约为0.90UCL;而红色区域(I区)则包含了缓冲层以及处于法向高度较低区域的发卡涡包结构,其平均模态速度约为0.79UCL。关于模态速度的统计分布,I区模态速度分布最宽,大概在0.65UCL至0.95UCL的速度区间内;而III区模态速度分布相对较为集中,通常位于0.90UCL至1.10UCL区间范围内。各等动量区在模态速度分布上存在一定重叠,I区和II区分界位置在0.85UCL,II区和III区分界位置在0.95UCL,而I区和III区之间的模态速度重叠区域较少而能较好分离。在本文后续关于等动量区的讨论中,默认以0.85及0.95倍槽道中心速度为分界。
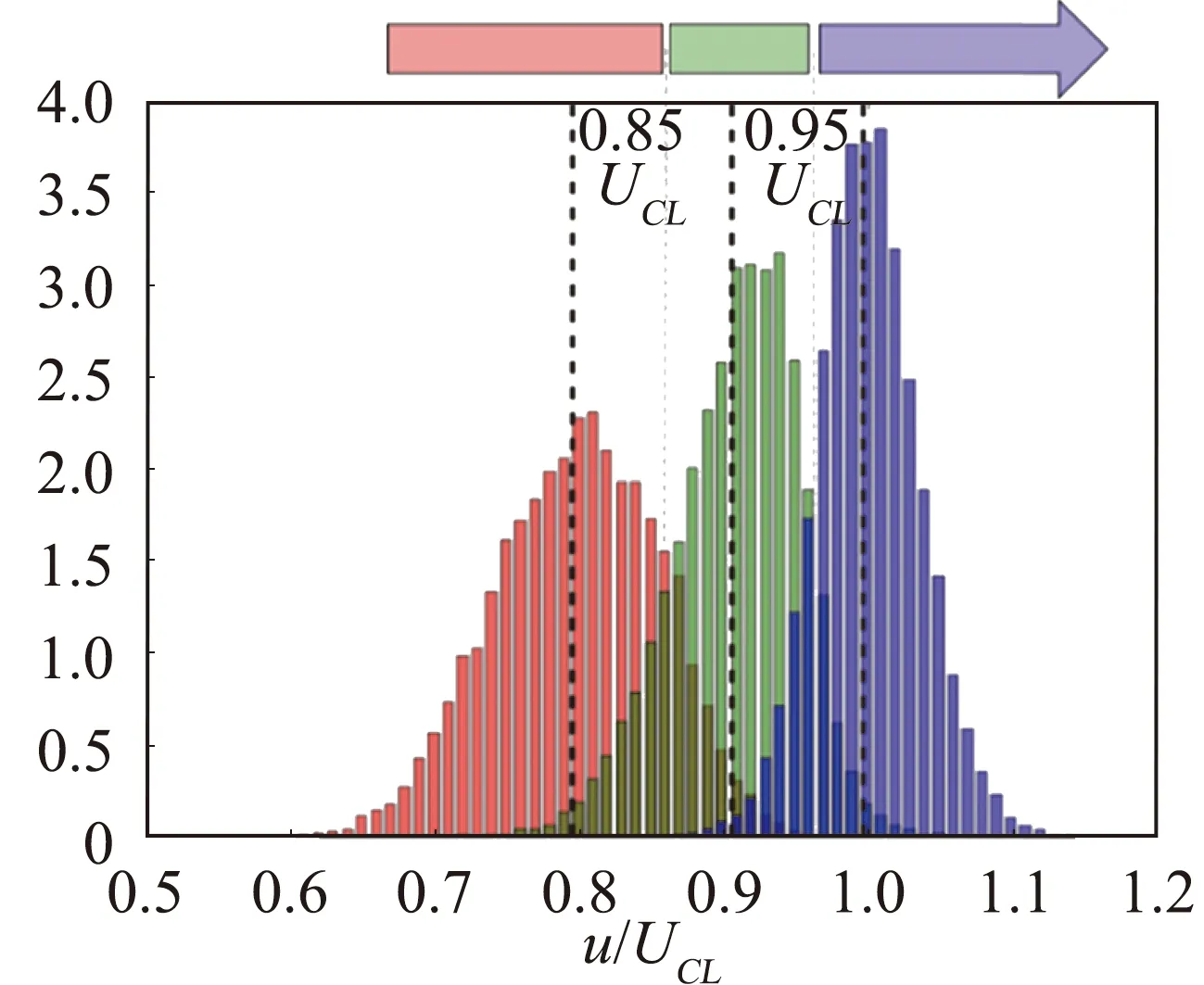
图3 模态速度概率分布。I区、II区和III区分别采用红、绿和蓝色表示。邻区分解的速度阈值分别为0.85UCL和0.95UCLFig.3 Distributions of modal velocity, zone I, II and III are respectively displayed in red, green and blue color. The threshold velocity between adjacent zones are 0.85UCL and 0.95UCL
图4显示了某一y-z截面上瞬时流向速度分布云图,黑实线为u=0.85UCL和0.95UCL的等值线,从图上可以看出,这两个速度阈值很好地区分出三个等动量区。
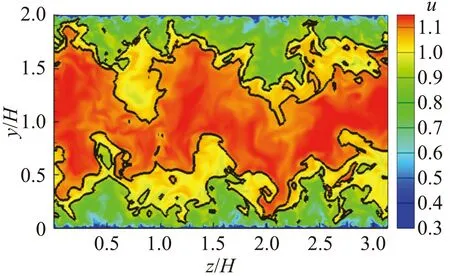
图4 瞬时流向速度在某y-z截面上的分布云图,其中黑实线为u=0.85UCL和0.95UCL的等值线。Fig.4 Distribution of instantaneous streamwise velocity in a y-z plane. Black lines: u=0.85UCL and 0.95UCL

(a)

(b)
2.3 等动量区湍流统计量
采用上述等动量区的模态提取方法,对Reτ=1000的槽道湍流进行了等动量区划分。图6显示了各等动量区内流向速度和浓度的统计分布。对于平均流向速度,如图6(a)所示,在y/H>0.2外,各等动量区内平均速度沿法向的变化较小,且邻区内的平均速度差异大致为0.1UCL。在近壁y/H<0.1范围内,I区的平均速度剖面基本能够和全场平均速度剖面吻合,说明在近壁由黏性主导剪切效应较强的区域,基本会被分到离壁面最近的等动量区范围内。图6(c)显示了各等动量区内平均浓度分布,同样在y/H>0.2呈现沿法向分布基本不变的规律,说明槽道湍流中的外区平均浓度,主要取决于其所处的等动量区层级而非法向高度,各等动量区流场状态的一致性也保证了浓度呈现较为统一的分布,III区平均浓度最高, I区平均浓度最低,相邻等动量区之间的浓度差异大致为0.04倍的全场平均浓度。图6(b)为各等动量区内流向速度脉动均方根的分布,其中脉动值是相对于各自区域内的平均值来计算。II区和III区范围内,速度脉动同样在外区基本不随法向高度变化。而I区从壁面到槽道中心,由于黏性作用逐渐减弱、速度梯度降低,使得脉动均方根逐渐衰减。图6(d)为浓度脉动均方根的法向分布,也呈现显著的浓度脉动关于等动量区间分层分布的规律。核心区内的浓度脉动量最小,而靠近壁面的I区脉动量最大,且各等动量区范围内浓度脉动在外区均会随着壁面高度逐渐减弱。

(a) U
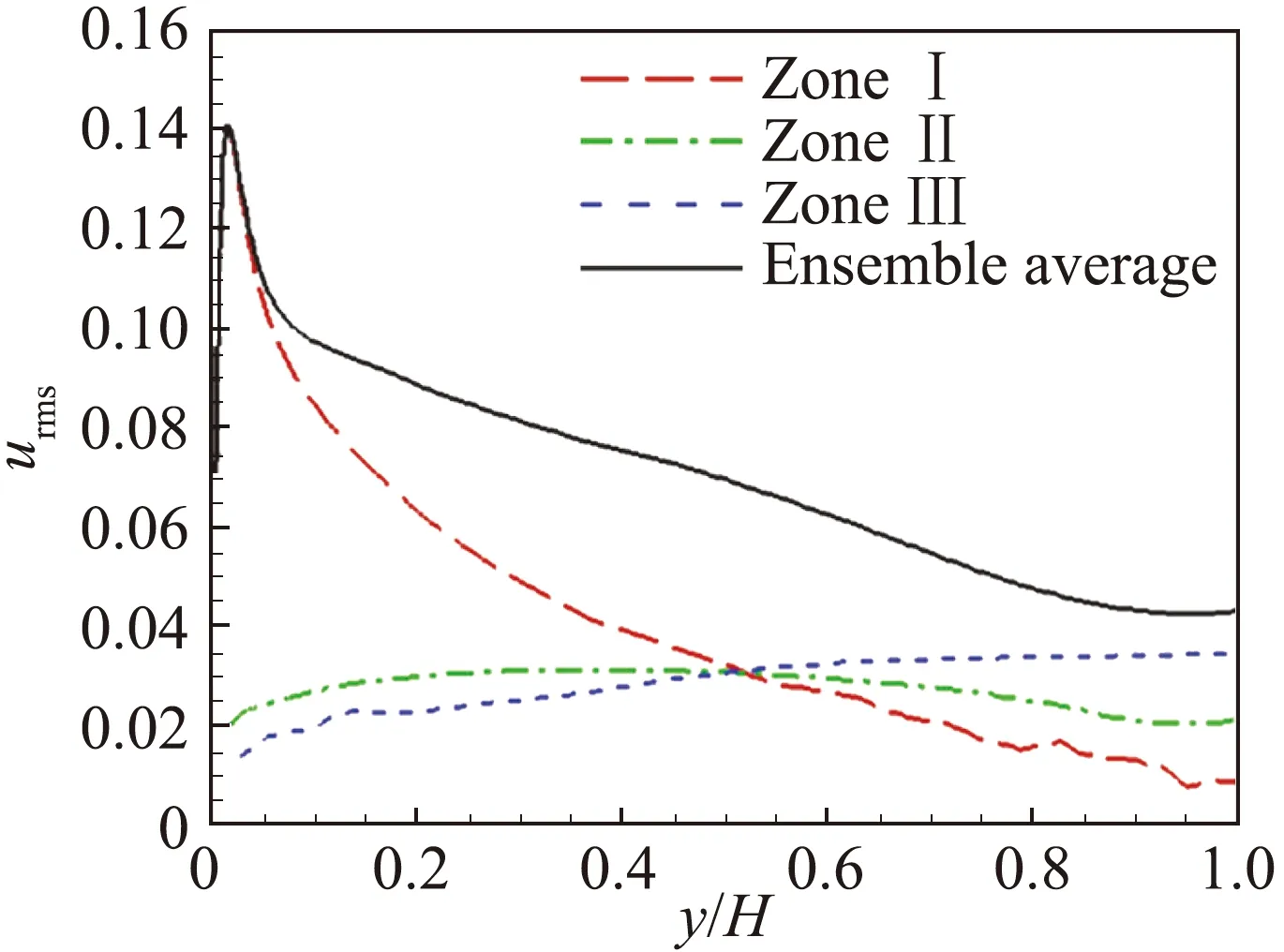
(b) urms

(c) C
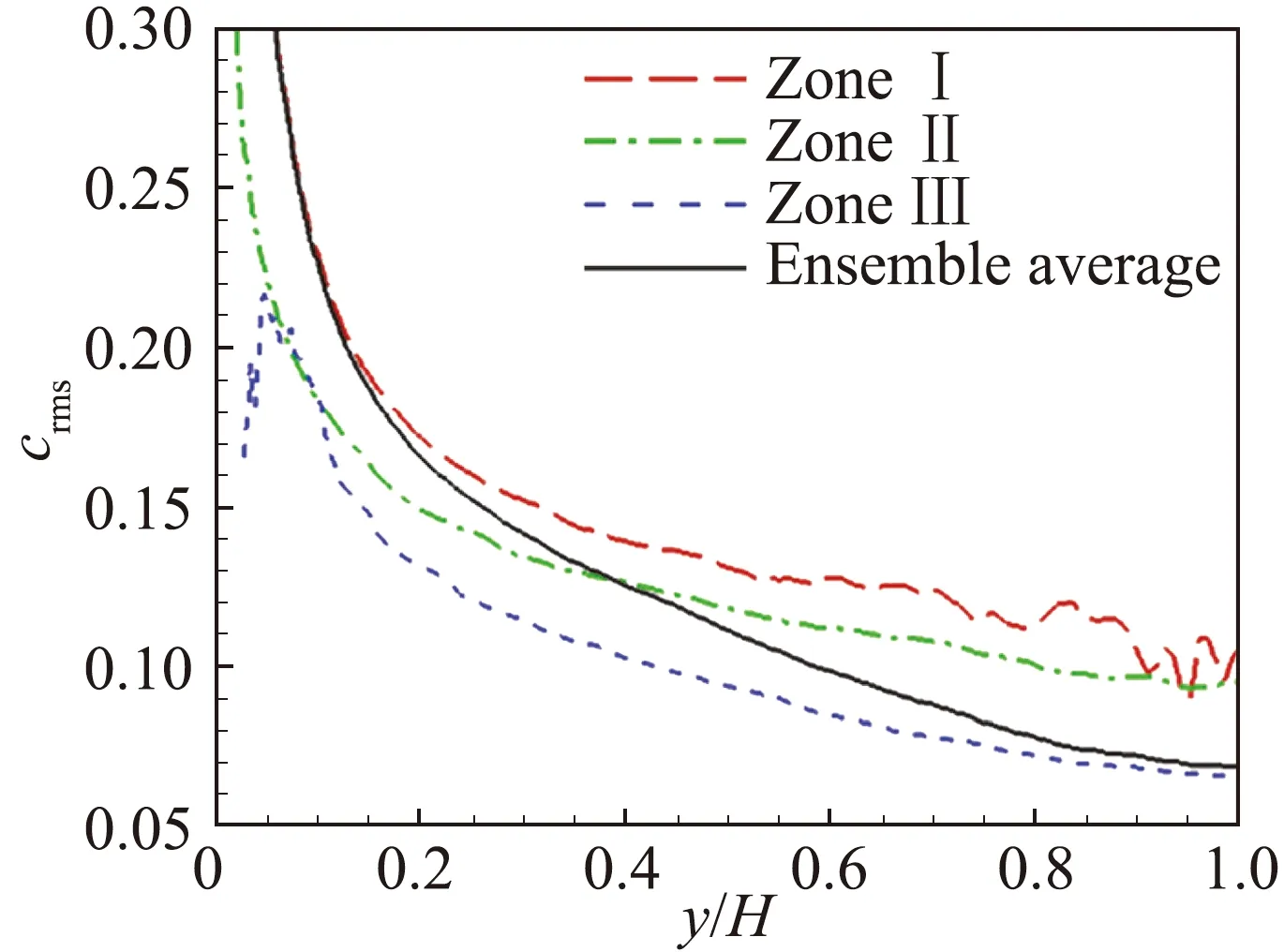
(d) crms
下面我们利用流型的拓扑分类来讨论不同等动量区的流动结构及浓度分布。基于临界点理论的流动拓扑分类是Chong等人于1990年提出的[33],若速度梯度张量的三个不变量为P,Q和R,对于不可压缩流动,第一不变量P=0,则在由第二不变量Q和第三不变量R构成的平面上,可将流动分为4种流型。若速度梯度张量特征方程的判别式为D=(27/4)R2+Q3,则由D和R构成的四个象限分别代表了不稳定的焦点/压缩、稳定的焦点/拉伸、稳定的节点/鞍点/鞍点和不稳定的节点/鞍点/鞍点流型。下面我们选取y/H=0.4处的流场进行讨论,在该处属于等动量区I、II、III的事件所占的比例分别约为25%、50%、25%,如图5(a)所示。
首先在QR平面上研究三个等动量区湍流结构的概率分布,如图7(a)、(c)、(e)所示。由于I区包含了较多的流向涡及近壁区发卡涡结构,因而QR分布较广,并且表征涡结构的第二象限概率明显大于其它区域。通常认为核心区(III区)已经位于发卡涡包范围之外,湍流脉动处于相对较为安静的状态,因而对应的QR概率分布相对更集中于原点附近,同时在第二象限中的概率占比也相对较小。受不同流动结构的影响,各等动量区内的颗粒浓度分布也存在较大的差异,如图7(b)、(d)、(f)所示。从浓度数值上看,QR分区中各等动量区的浓度最大值均约为1.05倍的当地平均浓度。差异主要在于高浓度对应的QR范围,核心区中高浓度部分占比最大,而I区占比最小。而对于低浓度事件,核心区与非核心区的差异则较为显著。核心区内的浓度极小值均在0.70倍平均浓度以上,而对应于非核心区的两个等动量区,浓度极低值均能达到0.60倍平均浓度以下。这也进一步说明,在发卡涡较为活跃的非核心区内,由旋转效应导致的浓度减弱要强于由剪切效应导致的浓度增加。综上所述,模态速度较大的等动量区,由于涡事件的减少使得浓度极低值增加,高浓度区域范围扩大,从而形成平均意义上整体浓度的增长和浓度脉动的减弱。
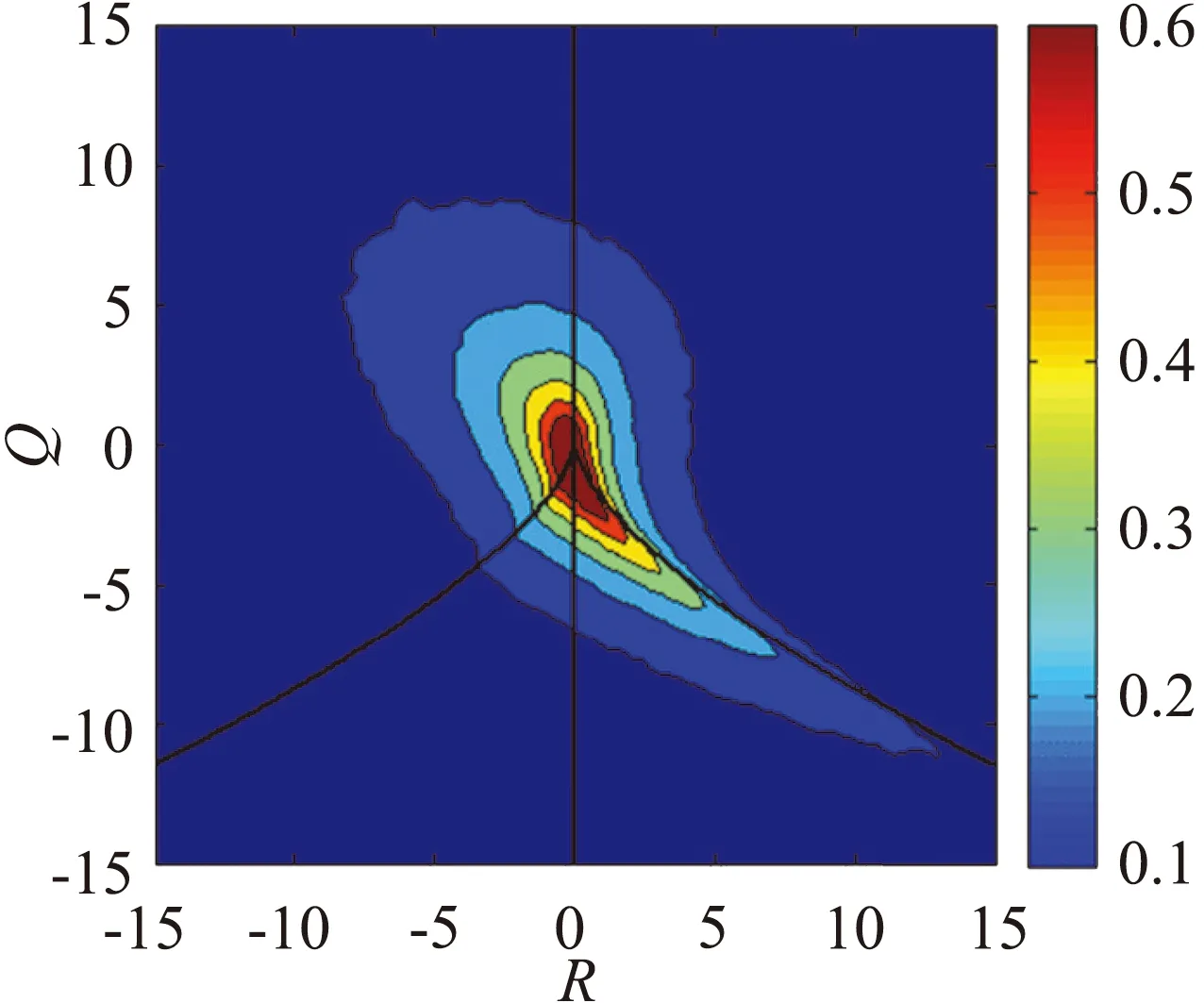
(a)

(b)

(c)

(d)

(e)
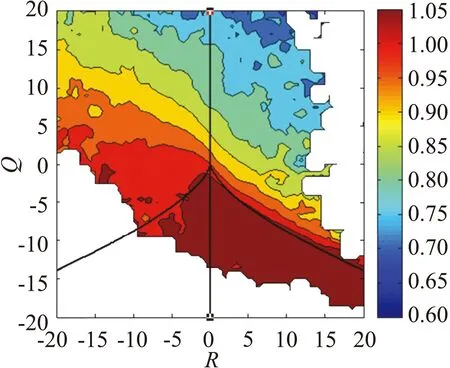
(f)
图7 在y/H=0.4处各等动量区内流动拓扑分类和浓度分布。
(a-b) I区,(c-d) II区,(e-f) III区;(a、c、e)QR联合累计概率,(b、d、f) 条件统计的浓度分布
Fig.7 Flow topology and the particle concentration in each UMZ aty/H=0.4. (a-b) Zone I, (c-d) Zone II,
(e-f) Zone III; (a、c、e) Cumulative joint probability ofQandR,(b、d、f) Conditional relative concentration
2.4 界面处湍流特性和涡结构
通过上述分析可知,对于不同的等动量区,速度场及浓度场的统计性质存在较大差异,而等动量区界面处存在着流向速度突变所形成的高剪切层。本节将采用条件统计的方法定量考察在核心区与非核心区交界面(II区与III区界面)附近,流场及浓度场统计性质。以下分析中,ζ为相对于等动量区界面的法向坐标,界面处ζ=0,ζ>0指向槽道中心的方向。核心区与非核心区的交界面由流向速度为0.95UCL的等值面给出,对于在法向存在多个取值点的情况,选取靠近槽道中心的点作为界面位置[9]。
图8显示了界面两侧0.2H范围内,速度和浓度的平均值及脉动均方根的分布。在图8(a)所示的平均速度分布中,界面位置处平均速度为0.95倍槽道中心速度,且在界面处存在阶跃性变化。界面两侧大于0.03H的法向范围以外,速度的法向变化则相对较为平缓。对于平均浓度,如图8(c)所示,在界面两侧也存在阶跃性变化,核心区相比于非核心区,平均浓度约有4%的提升,在界面下方0.03H处存在局部的浓度极小值,其成因与界面处存在的展向涡结构有关,在下一节进行进一步讨论。对于速度脉动,如图8(b)所示,界面以下的非核心区范围内,流向速度脉动均方根随着靠近界面呈现单调递减的变化规律,在界面以上的核心区内,速度脉动变化较缓,且脉动强度显著小于非核心区。在界面两侧,浓度脉动同样存在较大差异,核心区内的浓度脉动平均值大约能够下降至非核心区内的一半,如图8(d)所示。
由于核心区/非核心区界面处流向速度的阶跃性变化使得该处存在较强的平均剪切,在界面附近存在大量的展向涡结构。与平均剪切一致的展向涡,称之为顺向展向涡,与平均剪切相反的展向涡,称之为逆向展向涡。采用λci来识别涡结构,并统计其在空间中连通域的数量来反映涡结构的个数。本文采用该方法识别并统计了顺/逆向展向涡的个数沿法向的分布,图9(a)显示了x-y平面上H2面积内顺/逆向展向涡个数沿法向的分布,在各法向高度位置,顺向展向涡的数量Πp均大于逆向展向涡的数量Πr,其中逆向涡的数量在y>0.05H后基本不再变化,而顺向涡在近壁区出现概率最高,并且数量会随着法向高度逐渐衰减。图9(b)为核心区/非核心区界面附近的展向涡数量的统计结果,其与全槽道的统计结果相比存在显著差异。在界面位置处,顺向展向涡占主导,并且数量达到峰值,在界面两侧,顺向涡数量急剧减少,在|ζ|>0.05H后,顺向涡数量基本不再变化,约为界面处峰值的1/3。界面上的顺向展向涡与发卡涡的涡头相对应,而界面两侧分别对应于不同的发卡涡层级[34]。随着离壁面法向高度的增加,发卡涡结构数量逐渐减少,从而导致了图9(a)中顺向涡数量沿法向高度的衰减。而对于逆向涡,其数量在界面处基本为零。

(a) U

(b) urms

(c) C
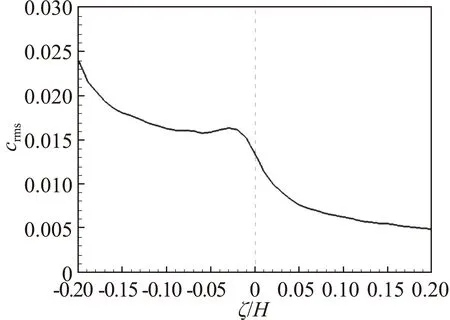
(d) crms
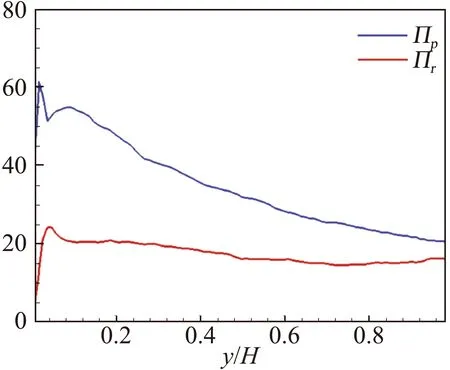
(a) 全槽道统计

(b) 核心区/非核心区界面附近统计
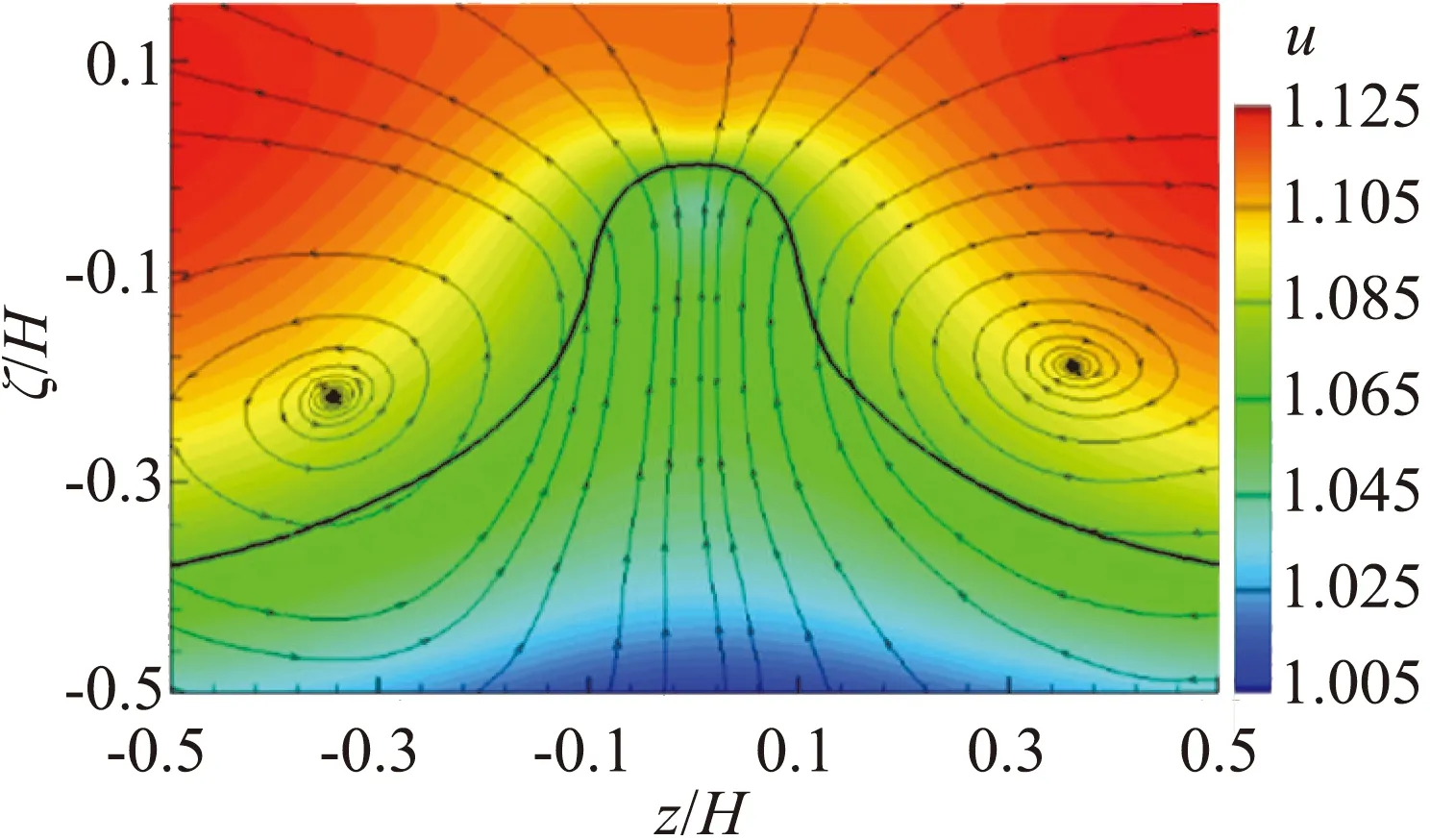
等动量区结构反映了发卡涡包内由不同层级的发卡涡结构诱导形成的速度阶梯分布。位于等动量区界面处的展向涡则对应于发卡涡的涡头,并由于涡头位置存在薄剪切层从而形成了较强的速度梯度。图10显示了条件统计的x-y平面上等动量区界面附近的涡结构及浓度分布。图10(a)中的云图为速度梯度张量的第二大特征值λ2,通常λ2<0零的区域被判别为涡结构区域。该图中界面处存在明显的λ2的极小值,对应于流线所显示的涡核处。该处的浓度分布如图10 (b)所示,界面上方核心区内的平均浓度远大于界面下方的非核心区,并在界面下侧存在颗粒浓度局部极小区域。
2.5 大尺度颗粒浓度结构
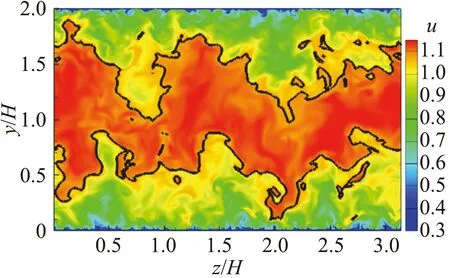
通过上述分析,我们发现在等动量区的界面处,速度场及浓度场均会发生跳跃性变化,位于核心区内的颗粒浓度会显著大于非核心区,而浓度脉动明显小于非核心区。图11显示了一个典型的y-z平面上瞬时流向速度和颗粒浓度脉动包络的分布,黑色粗实线为流向速度等于0.95UCL的等值线,表示核心区/非核心区的边界。由图11(a)可以看出,该边界很好地区分出了核心区和非核心区,也很好地区分出高浓度脉动和低浓度脉动区。

(a) λ2

(b) c
(a)
(b)
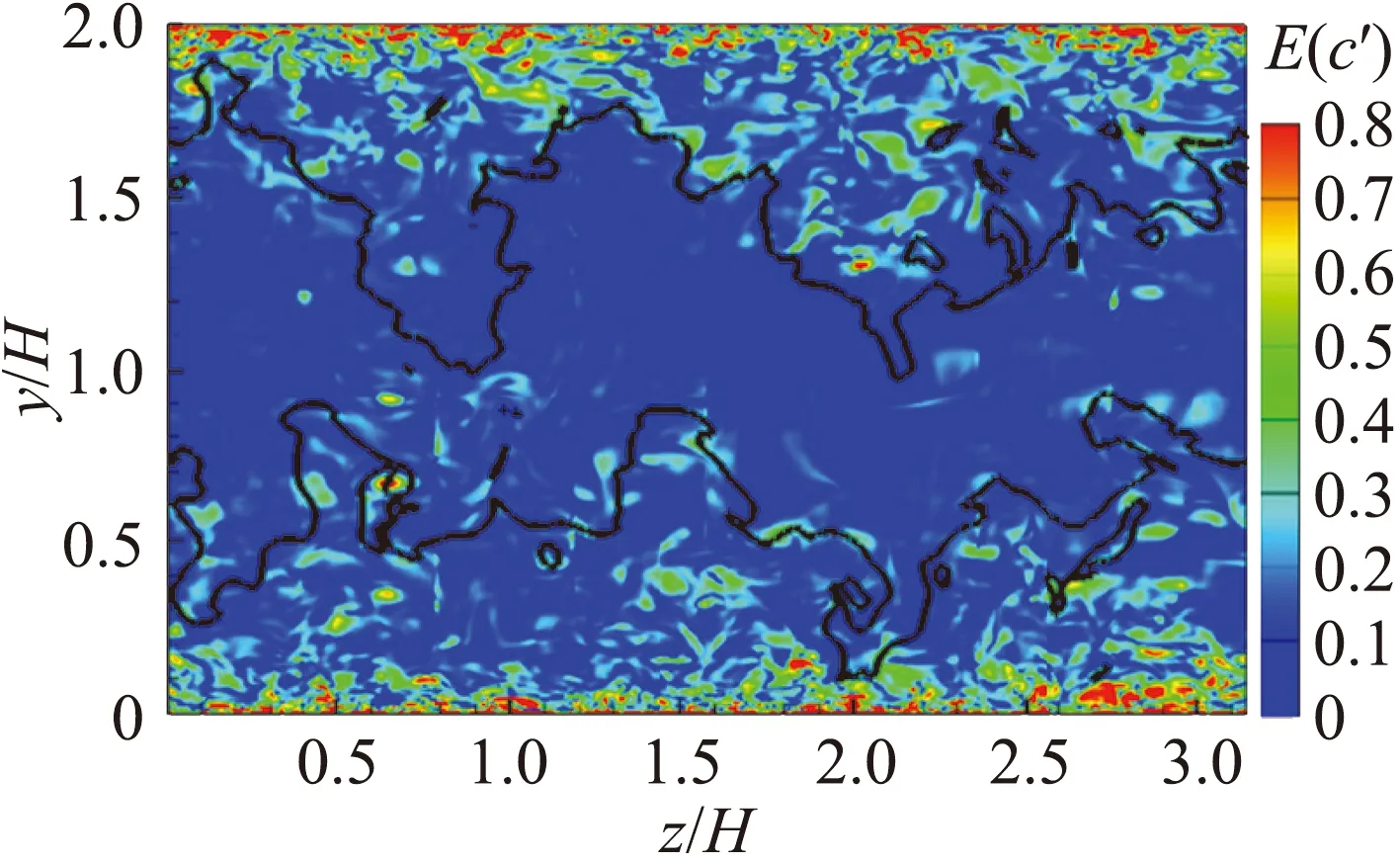
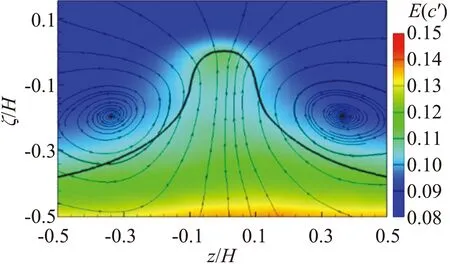
瞬时速度和浓度分布的空间一致性表明在外区颗粒分布也可能存在类似速度分布的大尺度结构。我们选取位于平均位置一倍标准差以上的核心区/非核心区界面(y/H>0.86)进行条件统计分析。图12(a、b、c)分别显示了条件统计的流向速度u、浓度c及浓度脉动包络E(c′)的分布,黑色粗实线为核心区/非核心区的界面。对于速度分布,如图12(a)所示,在界面下方存在较大片的低动量区。而对于浓度及浓度脉动包络的分布,发现其等值云图分布均基本贴合界面的变化。界面下方存在着大片低浓度及高浓度脉动的区域,其展向尺度约为H,而法向尺度约为0.5H。在较高位置的界面下方,存在层级分布的发卡涡结构,这些涡结构引起的强烈的速度脉动造成了强烈的浓度脉动,形成了与速度等值线外形贴合的浓度大尺度结构。另外,惯性颗粒倾向于聚集在低涡量区,在界面下侧由于存在大量的发卡涡结构,从而造成了低浓度分布。在展向中心紧贴界面的下方,存在一个局部的低浓度区,这是由界面处的展向涡造成的。
(a)

(b)
(c)
3 结 论
本文采用平衡欧拉法对含颗粒槽道湍流进行了直接数值模拟,流动的摩擦雷诺数为1000,颗粒Stokes数为1.0。采用高斯函数叠加法提取了等动量区的模态速度,进一步将流动划分为三个等动量区。对各等动量区的流体速度和颗粒浓度进行了统计分析,发现核心区平均浓度较高,而浓度脉动较低。等动量区界面处,速度与浓度存在明显跃变。界面处存在正向旋转的涡结构,对应于形成等动量区的发卡涡包结构中涡头部分,并且界面处展向涡会引起局部的低浓度分布。在远离壁面处的核心区与非核心区界面下方,对应着尺度较大的附着涡包结构,其下方存在着大尺度的低浓度及高浓度脉动区域。
