可重构式机械臂运动构型与关节控制系统研究
2020-03-10,,
,,
(沈阳建筑大学机械工程学院,辽宁,沈阳 110168)
0 引言
目前,国外有很多对模块化机器人的研究且技术相对成熟,已有很多的典型结构[1-4],我国针对模块化机器人的研究尽管也有很多突破[5-9],但是在空间模块化机器人的研究上依然处于初步探索阶段。目前该领域的研究主要集中在如何确定模块构型、模块信息沟通和控制模型选择等方面[10]。在此,从机械臂的空间典型任务出发,研究机械臂的构型搭建,针对构型设计研究机械臂的关节控制器,以满足机械臂的控制需求。
1 机械臂构型分析
1.1 机械臂的模块分析
机械臂的模块分为运动模块、末端操作模块以及辅助支持模块3大类。运动模块负责完成机械臂任务的空间位姿调整等工作,末端操作模块搭载在运动模块末端完成抓取、螺钉更换以及堵漏等既定任务;辅助模块为任务提供所需的必要辅助作业。具体分类如图1所示。
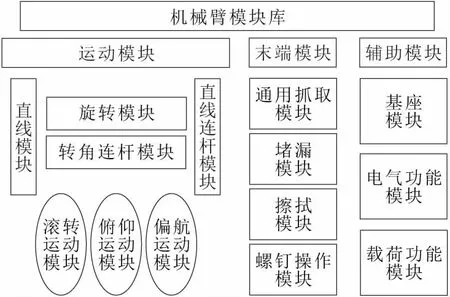
图1 机械臂模块分类
运动模块可以实现机械臂关节旋转和平移2种运动形式。空间旋转运动包括俯仰运动、滚转运动和偏航运动等。为简化构型组合情况,同时满足运动要求以及模块精简高效的目的,其空间基本运动可通过转角连杆模块与旋转单元模块的不同组合来实现,运动模块的组合如图2所示。偏航运动可由转角连杆与旋转模块实现,也可以通过运动模块的组合实现,可根据任务情况选用。直线运动模块通常搭载在滚转运动模块的末端,能够完成空间某方向的直线移动,可增加工作范围,提高操作精度。

图2 运动模块的拆分示意
由旋转模块与转角连杆模块构成的空间旋转运动形式,可同时完成姿态调整以及末端模块的定位,其运动空间以及折叠性能良好。直线模块通过平移运动完成姿态调整,具有一定的工作空间拓展能力,但是大面积使用会导致整体体积变大,以及折叠性能和稳定性减弱。借鉴国内外现有成果以及虚拟样机的设计,在任务构型选配时,可以考虑:主要的运动形式由旋转模块完成,使用直线连杆模块适当调整空间运动的组合顺序,根据任务的精准性要求以及可达空间情况可在模块后端适当位置加入直线模块辅助任务完成。
1.2 机械臂典型任务构型分析
机械臂的构型选择是基于任务需求出发的,针对每一种典型任务都可以搭建出多种机械臂构型,需要根据任务情况选出最优构型。最优的机械臂构型往往需要考虑如下因素:空间自由度,关节类型和数目,模块的组合顺序等。尤其需要机械臂实现避障时,要有足够的灵活性,考虑是否需要冗余的构型。以螺钉操作任务为例,如图3所示。在该项任务实施过程中,搭载在机械臂末端螺钉操作模块需要进行螺钉库的更换与准备工作,然后根据目标所在位置在各个运动模块的作用下完成空间的位姿调整以及越障等空间运动。到达目标位置附近后进行微调以及定位,最终由末端模块完成对应的螺钉拆装任务。

图3 螺钉任务场景
根据任务场景分析可知,在进行任务操作过程中,机械臂要在平台坐标系中能进行水平回转来调整整体的方向位置,肩弯曲与肘弯曲需要2个自由度保障平稳越障,腕部为保证末端模块的定位以及操作要求应保证至少3个自由度,在该任务条件下构型拥有6个自由度就能够满足机械臂位姿需求。假定机械臂的工作空间可满足基本任务要求,前端模块和末端模块分别选用基座模块和螺钉操作模块,搭建可满足要求的常用构型如图4所示。
构型A为运动模块最典型的组合模式,由俯仰运动模块-滚转运动模块-俯仰运动模块-末端操作模块搭配而成,其运动的实现均由俯仰与滚转模块配合完成,该构型具有良好的折叠型,运动学方程容易建立,但是操作灵巧性稍差,无法满足末端模块对相对位姿的要求。构型B与构型A相似,在末端操作模块前加入了直线模块,提高了末端模块某空间方向的工作延展空间,提高任务的精准性,该构型稳定性和折叠型相对构型A有所减弱。构型C的组合形式为俯仰运动模块-直线连杆模块-俯仰运动模块-直线连杆模块-俯仰运动模块-滚转运动模块-偏航运动模块的组合形式。该构型通过直线连杆模块替代旋转模块将两转角连杆通过直连方式进行连接,调整了运动模块的使用顺序。该构型拥有3个平行的轴线,其前端运动模块的工作空间较大,易于实现位姿的调整和空间避障,更适合在狭小空间条件下螺钉的安拆。综合考虑运动灵巧性、操作能力、可折叠型以及构型的简易性等,在螺钉操作任务中选用构型C。
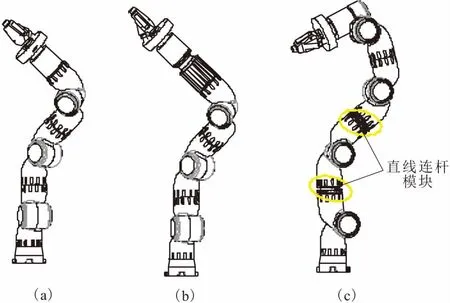
图4 螺钉操作典型构型
2 机械臂构型关节控制系统
2.1 控制系统框架
机械臂在构型选定后需要搭建其控制系统,功能模块的通用性由模块统一机械接口结构保证,其关节控制器也需要通用接口。搭建图4构型C的控制系统。采用基于CAN的分布式控制系统。各个关节控制器构成机械臂的基本控制单元,上位机将控制信号由总线传送至关节控制器控制电机动作,机械臂完成各种动作,各种传感器构成机械臂的信号反馈系统。各关节模块控制器结构如图5所示,其他模关节控制器结构与模块1的控制器类似,各关节模块的控制板和驱动板构成关节电气系统的硬件结构。同类关节选用相同的控制器,用以实现总线通讯,完成电机的运动控制以及各关节内部传感器及保护装置的信号处理。
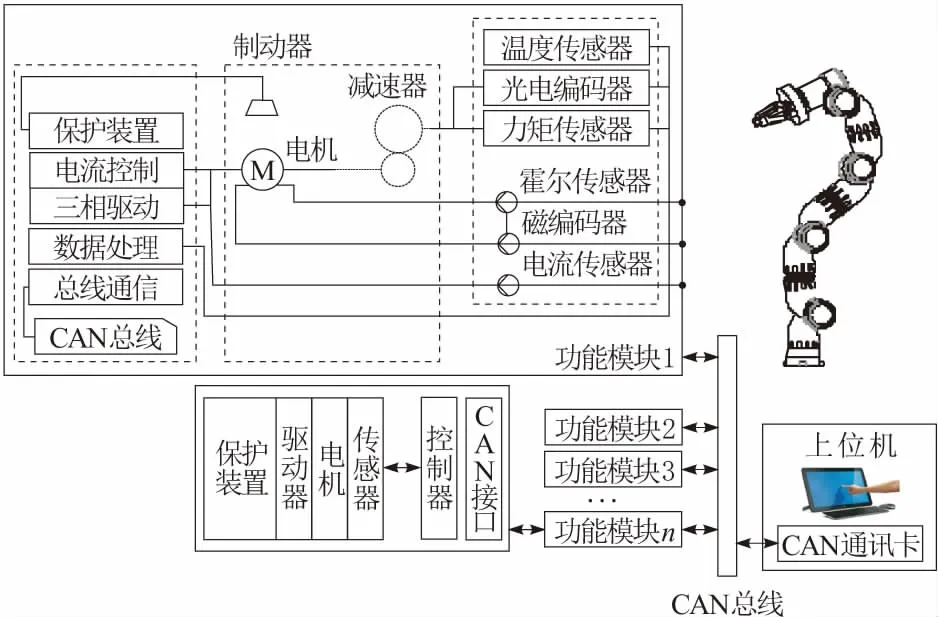
图5 控制系统示意
2.2 关节机电系统
旋转模块是机械臂构型的基本运动单元,其控制器作为最小关节机电系统是机械臂的基本控制单元,主要由相配合的3部分外壳、内部传动链以及传感系统构成,其结构如图6所示。旋转单元由放置在第1外壳内的无刷直流电机驱动,减速器的输出端与设置在第3外壳上的扭矩传感器相接,用于监测输出转矩防止过载。电机内部的霍尔传感器以及电磁编码器监测电机轴的相对位置,反馈关节的绝对位置信息。三相驱动中的电流传感器监测电流峰值,为实现关节在失电情况下的制动,在输入端还设置有制动器。设置在模块中的温度传感器监测温度变化,以避免突然的升温或降温对系统造成不可逆的损伤。第1外壳与第3外壳均可直接连接其他模块,承担机械臂的关节连接作用。
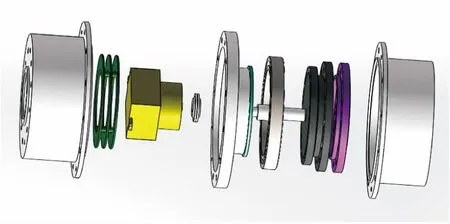
图6 旋转单元结构示意
2.3 关节电机模型
将旋转模块直流电机系统模型进行简化如图7所示。

图7 旋转单元电机物理模型
选用现代控制理论中的状态空间分析法进行系统模型描述。状态方程其多输入-多输出系统表达式为
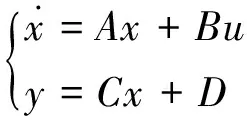
(1)
系统电路中电枢电流i、角速度ω和电机转角θ为3个独立变量,在这里选用3个状态变量x1,x2和x3,其他各参数情况说明如表1所示。即
(2)

表1 参数情况说明
假设系统无其他损耗,那么根据该电路建立方程为
(3)
于是状态空间表达式为
(4)
将系统参数带入,可得旋转模块控制系统传递函数
(5)
2.4 PID关节控制器
本设计中使用PID控制器,因为其参数易于调整,可以适应模块化机械臂对控制系统各方面性能的需求。控制器根据给定参考值与实际输出值所构成的控制偏差,将偏差经过比例(P)、积分(I)和微分(D)的组合作用形成控制量调整施加到系统中的功率,完成对被控对象的控制[11]。系统PID控制器的系统框图如图8所示。

图8 PID控制系统框图
3 参数整定
利用传统算法与智能算法相结合的方式改进PID控制器可以产生许多改进型控制器[12],本文将遗传算法结合传统算法对关节控制器的PID参数进行整定。在MATLAB中利用阶跃信号作为测试信号,分别利用改进的遗传算法和传统遗传算法进行计算,对比计算结果检验改进的遗传算法是否满足机械臂构型的控制要求。
3.1 基本遗传算法整定PID控制参数
遗传算法作为一种智能算法,不依靠任何先验知识,拥有高效的全局搜索能力,对于不便通过解析法求解的问题可以选用遗传算法解决。传统的遗传算法主要包括编码、适应度计算、交叉与变异等步骤。利用基本遗传算法进行参数整定:选定种群规模为50,交叉概率0.8,迭代次数100(其他指标见表2)进行参数初步整定。

表2 遗传算法参数
整定后的参数为:KP=15.768 7,KD=7.532 3,KI=1.199 8。以阶跃响应为测试函数,测试关节控制器性能,时间设定为1 s,得到图9所示的仿真结果,由图9可以看出采用传统的遗传算法其适应度函数收敛速度不是很理想,算法搜索过程迟缓。

图9 基本遗传算法整定情况
3.2 改进的遗传算法整定PID控制参数
3.2.1 Z-N法初步整定
由于被控对象传递函数已知,可利用Ziegler-Nichols方法中的经验公式法[13],进行初步整定。对给定的被控函数,选择其根轨迹图与z平面单位圆交点,求得增益Km,该点的ω即ωm,然后利用经验公式可得到初步整定参数,经验公式为
(7)
设定采样周期为0.2 s,在MATLAB中进行仿真,利用Z-N法得到的测试情况,如图10~图12所示。通过根轨迹与单位圆系统补偿前后,以及正弦函数的跟踪情况,可以看出经过初步整定后系统性能有所提升,但对满足系统要求还有一定差距。整定后的参数为:KP=9.202 7;KI=0.947 3;KD=22.349 6。
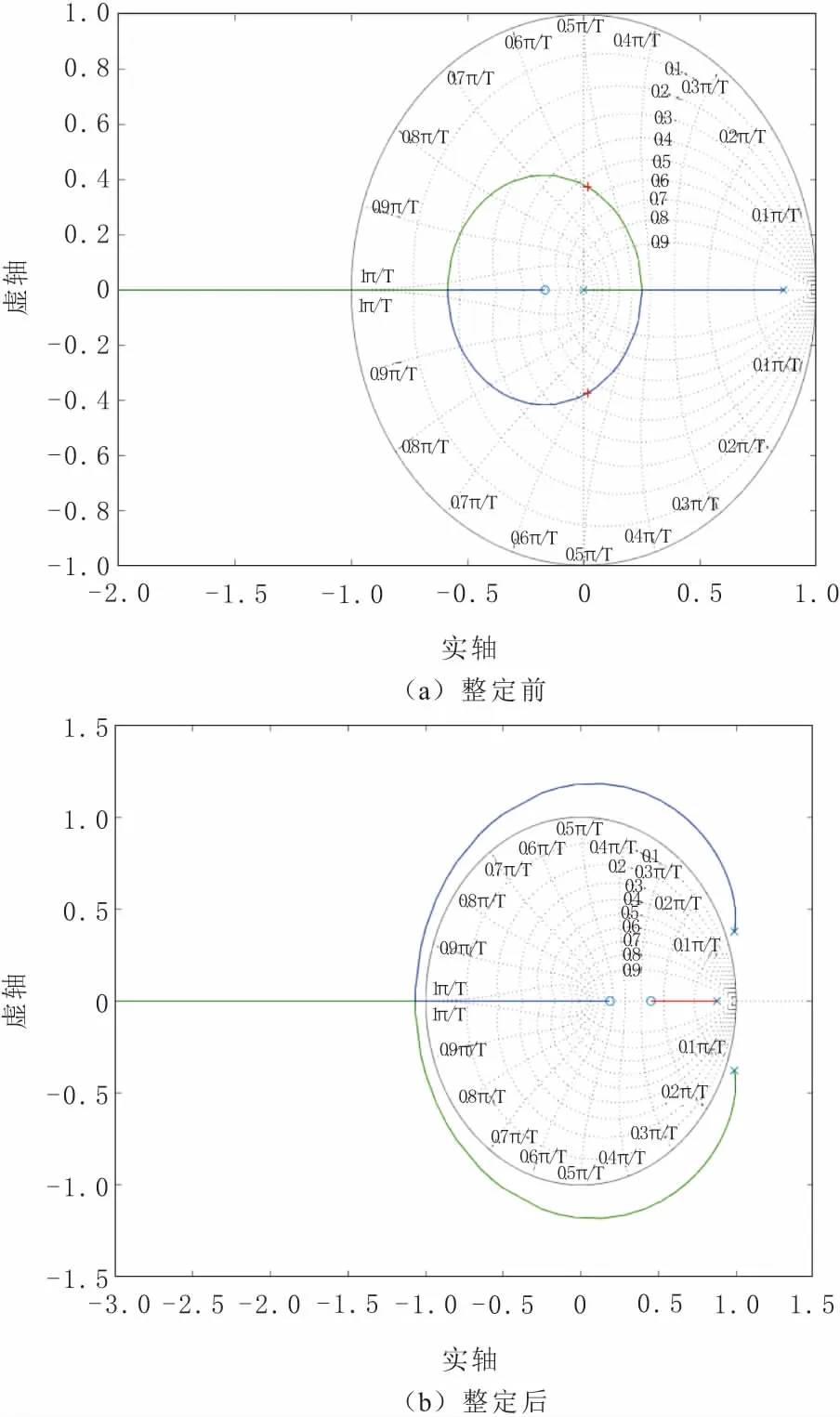
图10 根轨迹与单位圆比较
3.2.2 改进遗传算法整定PID控制参数
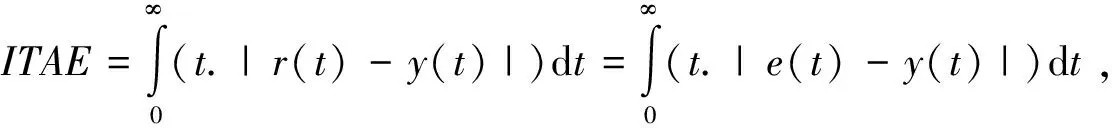
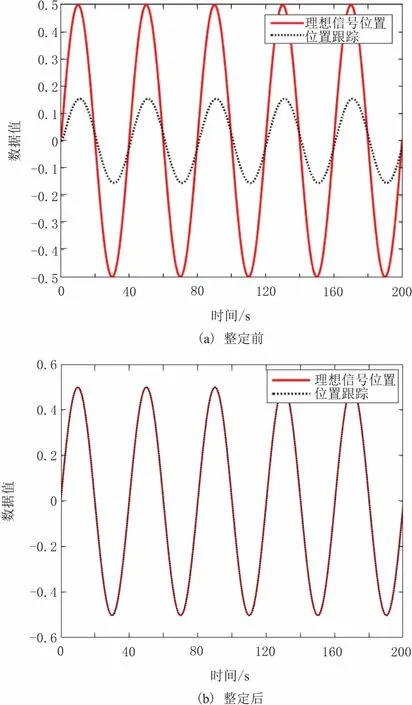
图11 正弦函数测试

图12 信号误差

图13 优化遗传算法整定情况
对比仿真结果可以看出,2种算法的阶跃响应效果均能满足要求,优化后的遗传算法对算法的收敛精度有了明显的提升,适应值也有一定的提升,这在一定程度上加快了系统的整定速度,可以保证系统的的优化效果。
4 结束语
针对机械臂的典型空间任务分析机械臂关节模块的运动特性,搭建机械臂构型并根据任务特点选择最优的机械臂构型。设计机械臂关节控制器并建立了关节模块的机电控制系统数学模型,采用Z-N法结合遗传算法优化关节控制器控制参数。仿真结果表明,利用该方法整定参数后的关节控制器响应速度快,满足控制系统要求。
