“微波技术基础”中传输线问题的教学探讨
2020-03-10胡金花张忠祥
胡金花,张 量,张忠祥
(合肥师范学院 电子信息系统仿真设计安徽省重点实验室,安徽 合肥 230601)
“微波技术基础”课程是电子信息工程专业本科学生的一门微波工程与射频技术专业方向课程,深入介绍导行电磁波传播规律和微波器件基本理论[1-2]。微波电路中有很多功能器件,研究这些器件时,主要讨论器件的频率、功率和阻抗。微波系统中传输的信号频率非常高,通常在吉赫兹数量级,对应的工作波长也就比较短,通常在厘米数量级。微波电路中元器件的几何尺寸通常在厘米到米数量级之间,与微波电路的工作波长相当,此时电路中的电流、电压与低频电路时有本质区别,电压和电流随时间变化的同时,也随位置变化,是时间和位置的二元函数,所以微波电路中任意一点都存在电阻、电容、电感和电导,因此,阻抗的概念在微波射频电路中十分重要。
在微波射频电路中,当负载与传输线不匹配时,就会有反射波,导致功率传输的效率非常低,当发生全反射时,信号就不能进入下一级元器件,微波电路也就无法正常工作。因此,阻抗匹配在微波电路中有着不可或缺的地位,其中λ/4阻抗变换器(transformer)是最基础的,也是最重要的匹配元件之一。
1 传输线理论
传输线理论[3-4]是在电磁场分析方法的基础上,利用低频电路分析方法进行求解,得到一般传输线方程,是研究微波技术的基础。电磁波在微波传输线中的传播现象可以看作是低频电路理论的延伸,也可以看作是麦克斯韦方程描述的一种比较特殊的电磁场情形。平行双导线是传输线主要结构型式之一,传输线其它复杂的型式都可以借助于这种简单的模型进行分析。
1.1 传输线方程
传输线方程是利用低频电路分析理论推导得到的基本方程,它表达了传输线上电压和电流的变化规律。由于微波频率较高,是分布参数电路,所以R1(电阻)、L1(电感)、C1(电容)和G1(电导)沿传输线处处存在。假设传输线的结构、材料以及所填充的介质等沿传输线的传播方向没有变化,则上述四个分布参数沿传输线就没有变化,这样的传输线称为均匀传输线。对于均匀传输线来说,采用“化场为路”的分析方法则比较简单。将均匀平行双导线看成由无穷多个小线元Δz(Δz≪λ)连接而成,则每一小段Δz就可以用低频电路理论[4]进行分析,等效电路如图1所示。
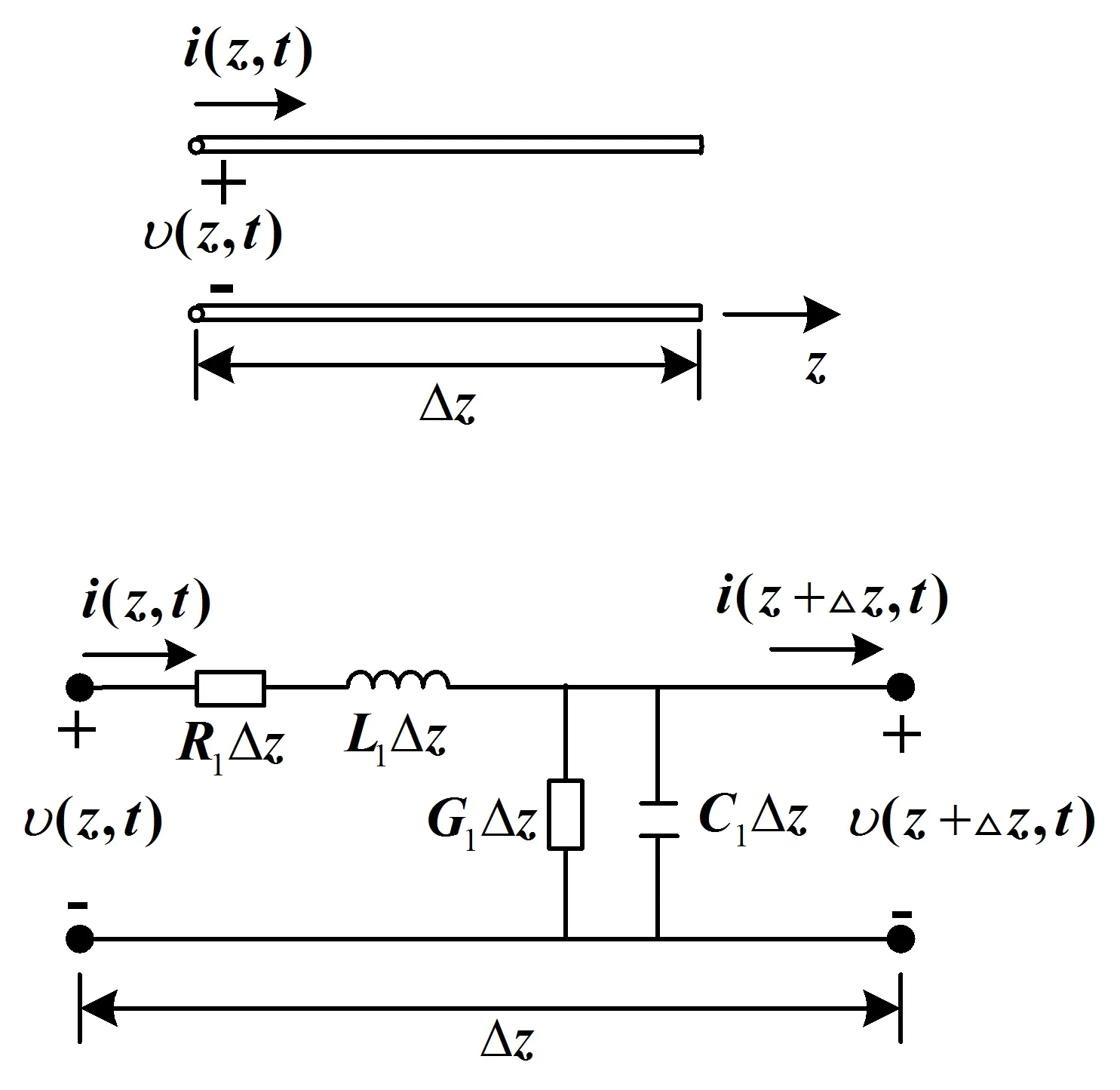
图1 长度为Δz的传输线等效电路
根据基尔霍夫定律[5-6]对线元Δz建立方程,然后对方程进行求解,即可得到以下两个近似方程
(1)
方程(1)是基本的传输线方程,也是比较经典的电报方程。
1.2 时谐传输线方程
对于简谐稳态传输线,传输线上每一点的电压和电流都是正弦函数的形式,那么电压υ和电流i可以用对应的相量形式来表示
υ(z,t)=Re{V(z)ejωt}
i(z,t)=Re{I(z)ejωt}
(2)
将表达式(2)代入方程式(1),整理可得:
(3)
为了求解,对(3)式再求导一次,可得
(4)
对于无耗平行双导线传输线,有R1=G1=0。方程(3)和(4)可进一步简化为:
(5)
(6)
结合方程(5)和(6)可求出电压和电流的通解为
(7)
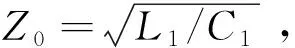
1.3 分布参数阻抗
如果已知一段长度为L的无耗平行双导线终端电压为VL,电流为IL,则可以求出沿线任意一点的电压和电流复振幅为
(8)
其中,d为负载到信号源方向的距离,且d=L-z。
由式(8)可得到无耗平行双导线上任意一点d的分布参数阻抗为:
(9)
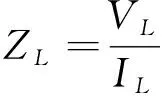
1.4 驻波比
均匀无耗传输线上的电压和电流,均有反射波存在,沿线电压和电流呈驻波分布。电压驻波比,用字母ρ表示,定义为传输线上驻波电压最大值(电压波腹点)与最小值(电压波节点)之比,也可以定义为传输线上驻波电流最大值(电流波腹点)与最小值(电流波节点)之比。电压驻波比和电流驻波比数值上一样的。由传输线理论可以推出,电压最大值和最小值的地方分布参数阻抗分别为Z0ρ和Z0/ρ。
1.5 反射系数
由于平行双线传输线在传输过程中存在反射波,为了表示反射波的大小,引入一个概念,即反射系数,用字母Γin表示。定义为反射波电压与入射波电压之比,也可以定义为反射波电流和入射波电流之比,具体表达式如下:
(10)
在表达式(10)中,V+和V-代表电压入射波和反射波,I+和I-代表电流入射波和反射波。
2 λ/4波长阻抗变换器
当微波组件之间的阻抗不匹配时,就会出现反射波,导致功率传输低,损耗大等问题。为了避免不必要的功率损失,需要消除或者减弱反射波,所以阻抗匹配对于射频电路而言十分重要。射频电路中的匹配网络有多种,其中λ/4阻抗变换器的应用是基础。当传输线的负载是纯电阻时,利用该变换器进行阻抗匹配比较简单。
2.1 负载为纯电阻
假设有一个无耗平行双导线传输线,其特性阻抗为Z0,它的终端接了一个阻抗为RL的负载载,并且RL≠Z0。此时传输线与负载是失配状态,传输效率低。为了实现匹配,在传输线与负载之间插入一个简单的匹配网络,使传输线无反射工作。如图2所示,一段长度为λ/4,特性阻抗为Z0的传输线就是最简单的匹配网络。
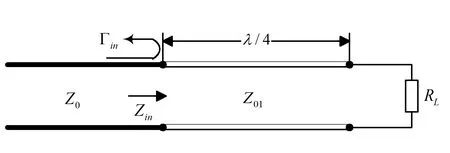
图2 负载为纯电阻时λ/4变换器
由传输线上任意一点的输入阻抗公式可得
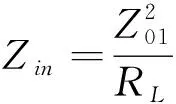
(11)
根据传输线匹配原理,则要求Zin=Z0,所以求出
(12)
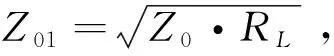
2.2 负载为复阻抗
在式(12)中Z01和Z0都是纯实数,所以λ/4阻抗变换器只能用于匹配纯电阻负载。当负载是复阻抗时,仍采用λ/4阻抗变换器进行匹配,则有两种处理方法。
第一种方法是把阻抗变换器的终端转换为纯电阻。由前面分布参数阻抗可知,终端开路(或者短路)的均匀无耗传输线的输入阻抗为纯电抗,可以抵消负载的电抗部分,电路如图3所示。
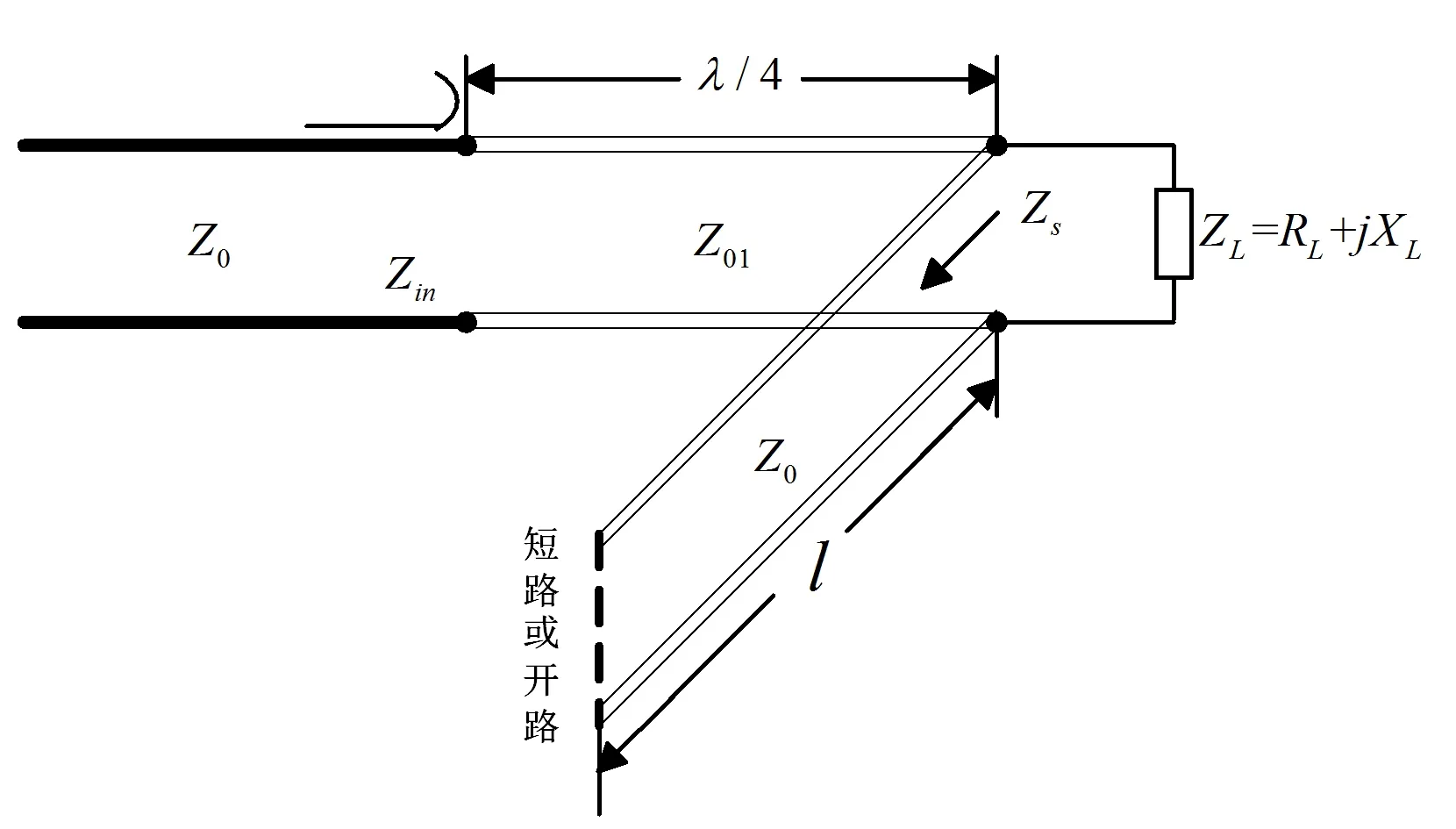
图3 负载为复阻抗时λ/4变换器
特性阻抗为Z0,终端开路、长度为l的无耗传输线的分布参数阻抗为
Zs=-jZ0ctgβl
(13)
式中j为虚数因子,β为相位常数。要使λ/4阻抗变换器的终端为纯电阻,则Zs应该抵消负载ZL中的虚部,由于Zs和ZL是并联结构,采用导纳计算比较方便。首先将负载阻抗转换为导纳,则
(14)
对终端开路、长度为l的无耗传输线的阻抗求导数,就得到对应的导纳为
(15)
比较 (14)和(15),可得
(16)
解得
(17)
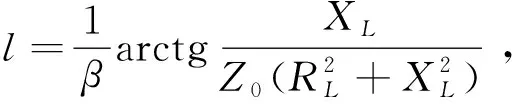
要实现无反射传输,应该满足Zin=Z0,所以求得
(18)
第二种方法是在原传输系统的电压波腹或者波节点位置插入λ/4阻抗变换器,如图4所示。
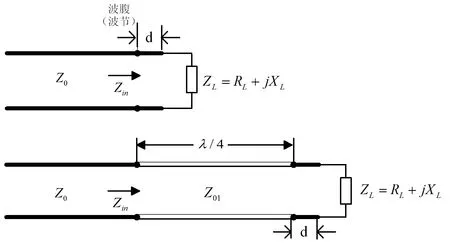
图4 波腹(波节)点接入λ/4变换器
由前面传输线理论可知,电压波腹点和波节点的输入阻抗是纯电阻。我们可以在波腹点或者波节点处接入λ/4匹配网络。当无反射匹配时,应该有Zin=Z0。若图4中接入点d处为电压波腹点,则得到λ/4线的特性阻抗为
(19)
若图4中接入点d处为电压波节点,则得到λ/4线的特性阻抗为
(20)
3 结语
本文首先介绍了“微波技术基础”课程的特点,然后从传输线理论出发,引入了传输线方程、传播常数、特性阻抗、输入阻抗、反射系数和驻波比等概念。在传输线理论分析的基础上,对λ/4阻抗变换器在不同负载情况下的匹配公式结合电路模型进行了详细推导。
