内河框架码头桩柱绕流水动力特性的二维数值模拟

刘明维，曾丽琴，陈 刚，沈立龙，牟治忠，王明镜

(1. 重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074；2. 重庆交通大学 水利水运工程教育部重点实验室，重庆 400074；3. 四川省交通运输厅交通勘察设计研究院，四川 成都 610000)

随着内河水运行业发展，框架式码头结构在长江上游得到广泛运用。与长江中下游及沿海高桩码头相比，内河框架码头具有结构构件尺寸大(相对于内河普遍使用桩柱直径来说，直径1.5～3.0 m属于大直径)、排架桩柱间设有多层纵横连系撑等结构特点。同时码头设施面临长时间(大于6个月)、大水深(大于20 m)、反复出现的大水位差(大于30 m)和大流速(大于2 m/s)等复杂水文环境[1]，码头结构阻水效应明显，特别是当码头位于流速大的山区河段，水流荷载可能会成为主导可变作用[2]。因此，需要系统研究内河框架码头桩柱绕流水动力特性，为准确计算码头结构桩柱所受水流荷载奠定基础。

针对圆柱绕流问题，国内外学者进行了一系列研究，CFD数值模拟方法被广泛应用。Ghadiri等[3]基于ghost-cell技术和Cartesian-staggered网格，利用标准模型及RNG模型分别研究了层流(Re=100/200)和湍流(Re=2.2×104)条件下串列双圆柱绕流尾流特性。Ong等[4]基于雷诺平均法对超高雷诺数(Re=1×106，3.6×106)条件下的圆柱绕流进行了二维数值模拟，得到了圆柱绕流水动力特性相关参数。刘松等[5]运用有限体积法，研究Re=200时串列双圆柱不同间距对圆柱间相互作用和尾流特征的影响，发现流动特征基本上取决于圆柱间距大小，两圆柱的斯特劳哈尔数基本相同。刘景伟等[6]研究了低雷诺数、桩间距对漩涡脱落形态、压力系数、斯特劳哈尔数的影响，发现随着桩间距的增加上游圆柱体的剪切层分离点位置逐渐后移，干涉效应消失。樊娟娟等[7]基于N-S方程与模型，对较高雷诺数(Re=1.0×105和2.5×105)圆柱绕流分别进行了二维与三维数值模拟，结果表明二维数值模拟的升力系数大于三维模拟结果。Prsic等[8]利用LES研究了实际近海结构物在绕流雷诺数Re=13 100时的近尾流流场特点及数值模拟参数的影响。周强等[9]利用LES方法对亚临界雷诺数下圆柱体尾流结构进行了三维数值模拟，给出了平均流场及湍流流场的流场特征，指出回转长度是尾流结构最重要的特征参数。贾晓荷等[10]基于三维大涡模拟方法，研究了定常流中Re=6×104和L=3D情况下不同排列的双圆柱绕流流场及圆柱受力，结果表明串列双圆柱的上游圆柱受力大于下游圆柱，下游圆柱的升阻力系数变化频率满足2倍关系，两圆柱的脱落频率、涡街相位相同；并列双圆柱的阻力系数基本相同，且变化趋势相似，涡脱频率接近单个圆柱，涡街相位相反。

目前，圆柱绕流的数值模拟研究多集中在亚临界雷诺数以下，对于超高雷诺数范围内桩柱绕流数值的模拟研究较少，对于实际工况(实际流速、桩径)下，内河框架码头桩柱超高雷诺数时的桩柱绕流水动力特性数值模拟研究则更少。本文依托重庆港果园码头二期工程，基于计算流体动力学方法，进行大流速下内河框架码头大直径单桩、串列及并列四桩柱绕流水动力特性二维数值模拟，系统分析不同流速及不同桩间距下桩柱绕流尾流流场形态、绕流阻力系数Cd、升力系数Cl、斯特劳哈尔数Sr等水动力特性参数的变化规律，为计算类似内河框架码头实际工程项目水流荷载提供参考。

1 数值模拟

依托三峡库区重庆港果园码头二期工程(结构见图1)。简化码头结构，取码头结构段中一处纵向串列4圆柱及横向一榀排架并列4桩柱进行二维数值模拟，桩柱直径D为2 m，计算模型如图2和3所示。其中串列4桩柱桩间距的变化范围为L=2D，3D，4D，5D，7D，9D，13D；并列4桩柱桩间距变化范围为L=2D，3D，4D，5D，7D，9D。流速U取洪水期1和2 m/s两种工况，即雷诺数Re=2×106和4×106。通过设置初始速度来控制流场雷诺数，流场进口采用速度入口边界，出口采用自由出流边界，上下边界采用对称边界，桩柱采用无滑移壁面边界。

图 1 果园码头二期工程Fig. 1 Phase Ⅱ project of Guoyuan wharf

图 2 串列四桩柱绕流计算模型及网格划分Fig. 2 Flow calculation model and mesh generation for four pile-columns in tandem arrangement

图 3 并列4桩柱绕流计算模型Fig. 3 Flow calculation model for four pile-columns in parallel arrangement

采用Gambit软件按实际尺寸建立模型，选取桩柱圆心为原点，在笛卡尔坐标系下表示计算域，X坐标轴正向与水流流向一致。圆柱桩径D为2 m，考虑进出口边界与上下边壁对绕流的影响，以整个计算范围合理适中为原则，设置圆柱距上游入口边界5D，距下游出口边界为20D，距左右边壁为5D，串列桩柱计算区域如图2所示。选取最左边桩柱柱体圆心为原点，从左至右依次为桩1、桩2、桩3、桩4，并列桩柱计算区域见图3。

由于所选取工况雷诺数处于超临界、过临界雷诺数范围，选用适应于高雷诺数的RNG k-ω湍流模型。选取基于压力耦合方程的二阶隐式求解，压力速度耦合选取PISO算法，压力采用标准法离散，动量、湍动能、湍动能耗散率采用二阶迎风格式离散。计算时间步长为0.01 s，每个时间步长内迭代计算20次，采用阻力的一般计算式得出阻力系数。采用四边形结构化网格划分计算区域，根据圆柱绕流的流场特点，靠近圆柱的区域流场形态复杂，同时也是研究中重点关注的区域，因此网格适当加密，远离圆柱区域，网格相对稀疏。

2 数值模型可靠性验证

2.1 桩柱水动力特性现场试验

为验证数值模型可靠性，开展了桩柱水动力特性现场试验研究[11]。码头上游第一榀排架中主测桩(如图4)受其他纵横连系撑和停靠船舶等综合影响因素最小，故选择该桩来研究单桩桩周水动力特性分布，主测桩上测试层位共4层，垂向总间距8 m。试验针对码头现场不同时间段多个排架、多个桩柱、多个层位及不同角度处84个点进行水流荷载数据采集，通过计算不同条件下桩周动水压力，求得大雷诺数(1×106～4×106)时桩柱绕流阻力系数范围约为0.30～0.45。

图 4 主测桩位置及定位件布置(图中φ1 500 mm是钢横撑直径)Fig. 4 Main testing pile position and positioning parts layout

2.2 模型结果验证

为验证所建计算模型、网格划分及模型参数选择的可靠性，先进行Re=2×106和4×106单圆柱绕流数值模拟，并将模拟结果与上述文献的研究成果进行对比分析(见表1)。由表1可知，模拟计算所得平均阻力系数符合现场水流荷载测试水流阻力系数结果，Cd，Cl，Sr等水动力特性参数与学者们的数值模拟结果较为接近(由于数值模拟中桩径、初始流速不同可能引起差异)，从而验证了本文中网格划分、参数取值及数值模拟结果基本准确。

表 1 单圆柱绕流计算结果与文献对比Tab. 1 Comparison between single-cylinder flow results and literatures

3 串列4桩柱绕流模拟结果分析

为进一步系统研究流速和桩间距对串列4圆柱绕流水动力特性的影响，分别对流速U为1和2 m/s即Re=2×106和4×106两种工况及L=2D, 3D, 4D, 5D, 7D, 9D, 13D等7种工况进行数值模拟计算，分析流速、桩间距对大直径桩柱绕流尾流形态，Cd，Cl，Sr等水动力特性参数的影响规律，探讨串列桩柱间的遮流影响。

3.1 桩间距变化影响

3.1.1 尾流流场形态 随着L的增大，下游桩柱与上游桩柱之间的干涉效应逐渐减弱，桩柱尾流呈现不同的漩涡脱落形式，如图5所示。

图 5 不同桩间距下串列4桩柱绕流瞬时速度云图(Re=4×106)(单位：m/s)Fig. 5 Instantaneous velocity cloud map of tandem pile-columns under different pile spacings (Re=4×106)(unit: m/s)

由图5可见，L＜4D时，随L逐渐增大，桩1、桩2(从上游至下游依次为桩1～桩4)后均开始形成完整的卡门涡街，说明桩柱间流场的相互干扰较小；故在桩间距[3D,4D]之间存在1个临界间距，影响着串列桩柱间涡街的形成；L＞7D时，桩1、桩2后的流场形态基本保持不变。上述串列4桩柱中桩1与桩2间的流场形态随L的变化符合Zdavkovich[15-16]的串列双圆柱绕流试验结果。桩4后流场的涡街随L的增大而减弱，涡街变得不明显，这是因为上游形成的漩涡能量逐渐转化为内能热能耗散掉，下游流场流速减小，Re进入临界区与超临界区，没有明显的涡街形成。

3.1.2 绕流水动力特性 绕流阻力系数Cd的变化如图6所示，在L=2D～5D时，各桩柱绕流阻力系数没有明显变化，说明桩柱间流场干涉强烈；在L=7D～13D时，各桩柱绕流阻力系数基本保持不变，桩1阻力系数稳定在0.46左右，桩2～4阻力系数稳定在0.33左右，说明随着L的增大，桩间流场的干扰减弱，对绕流阻力系数的影响减小。

绕流升力系数Cl的变化如图7所示，各桩柱绕流升力系数随L的变化曲线均表现出先减后增再减小的趋势。在L=2D～4D时，系数先减后增，且各桩柱系数从上游往下游依次增大，体现了串列布置对Cl的影响；L＞5D时，因为桩1位于最上游，桩间距大时其尾流基本不受下游流场影响，故Cl基本不变。

图 6 绕流阻力系数随桩间距的变化曲线(Re=4×106)Fig. 6 Change curves of drag coefficient around each pile with pile spacing (Re=4×106)

图 7 绕流升力系数随桩间距的变化曲线(Re=4×106)Fig. 7 Change curves of lift coefficient around each pile with pile spacing (Re=4×106)

斯特劳哈尔数(Sr)的变化如图8所示，可见，桩1～3的Sr随L的变化趋势相同，均是先减后增最后保持不变，桩4由于处于最下游，其流场受上游桩柱流场的影响较大，曲线变化趋势稍有不同。在L≥5D时，各桩柱绕流Sr基本不变，说明此时L的变化对串列4桩柱各桩的涡流没有影响。

《港口工程荷载规范》(JTS 144-1—2010)中为了简便计算串列各桩柱水流阻力，将串列各桩柱之间流场的相互影响用遮流影响系数来量化。根据计算统计给出不同桩间距时大流速下大直径串列4桩柱各桩柱的遮流影响系数(见表2)。

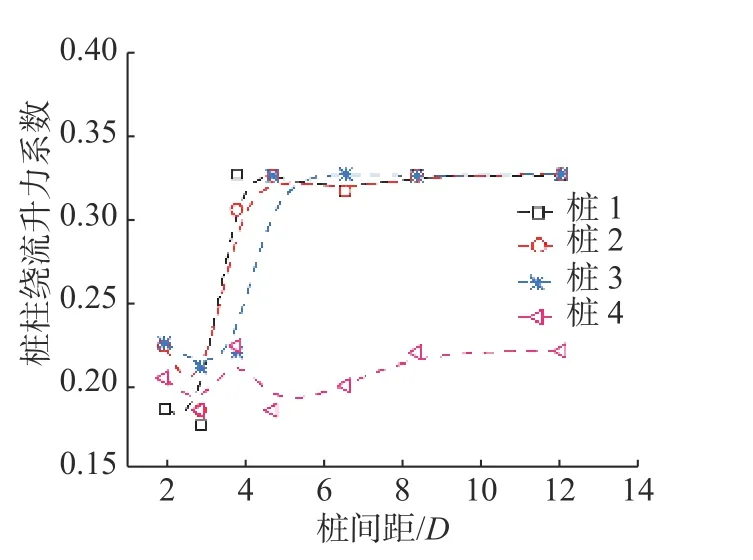
图8 各桩柱绕流系数随桩间距的变化曲线(Re=4×106)Fig.8 Change curves of flow coefficient of each pile with pile spacing (Re=4×106)

由表2可知，遮流影响效应在桩间距小时表现更明显，处于下游桩柱的绕流阻力系数明显小于桩1；在L≥7D时，遮流影响系数基本不变。当L较小时(L=3D～5D)的遮流影响系数大于桩间距较大(L＞5D)时的遮流影响系数，且L较小时桩2遮流影响系数最小，桩4遮流影响系数大于桩3和桩2，与Cd，Cl，Sr变化有关。L＞5D时，Cd，Cl，Sr基本不再变化，桩柱间流场干涉减弱，故桩间距小时的遮流影响系数大于桩间距大时的；L=3D～5D，各桩柱的Cd没有明显变化，桩柱间流场干涉强烈，Cl，Sr均增大，桩4由于处于最下游，其流场受上游桩柱流场的影响较大，遮流影响系数较大。

表 2 不同桩间距下串列4圆柱绕流各桩柱遮流影响系数Tab. 2 Influence factors of obstruction of each pile in tandem pile-columns under different pile spacings

3.2 流速变化影响

依托工程中L=4D为典型桩间距，分别进行洪水期特征流速为1和2 m/s情况下串列4桩柱绕流数值模拟，以此研究流速对串列4圆柱绕流水动力特性的影响。从图9可知，两流场总体形态基本相同，桩1～3后均有漩涡脱落，下游桩后涡街不明显，流场较混乱。由表3可知，流速变化对上游3根桩柱的绕流阻力、升力系数影响较小，对桩4的各主要系数影响大，在桩4后有完整涡街出现；对各桩柱的Sr影响较大，即不同流速下，各桩柱漩涡脱落频率不同。

图 9 不同流速下串列4桩柱绕流瞬时速度云图(L=4D) (单位: m/s)Fig. 9 Flow instantaneous velocity cloud map of four pile-columns in tandem under different flow rates (L=4D) (unit: m/s)

表 3 不同流速下串列4圆柱绕流主要系数统计(L=4D)Tab. 3 Statistics of main coefficients of flow around four cylinders in tandem at different flow rates (L=4D)

4 并列4桩柱绕流模拟结果分析

为进一步系统研究流速和桩间距对并列4圆柱绕流水动力特性的影响，分别对流速为1和2 m/s即Re=2×106和4×106两种工况及L=2D，3D，4D，5D，7D，9D等6种工况进行数值模拟计算，分析流速、桩间距对大直径桩柱绕流尾流形态和Cd，Cl，Sr等水动力特性参数的影响规律，探讨并列桩柱间的横向影响。

4.1 桩间距变化影响

4.1.1 尾流流场形态 如图10所示，各桩间距下整个流场都存在对称性(故下文只对桩1、桩2分析)。在L=2D时，桩1、桩2间空隙的流动明显偏向外侧，在双圆柱后形成1条较窄和1条较宽的尾流，形成偏斜流态；桩2与桩3间的空隙流动由于处于中间位置，两侧均有空隙流动，偏斜流态消失，整个流场对称。双圆柱绕流中的双稳现象[17]即偏斜流态随机在两圆柱间切换这种现象消失，空隙水流流动始终偏向外侧。上述结论符合Zdavkovich[15-16]的并列双圆柱绕流试验结果。桩柱尾流漩涡的脱落同步并表现出两种耦合方式，即同步同相和同步反相涡脱落。在L=2D～5D时，相邻桩柱绕流流场的漩涡脱落相位相反；在L=7D～9D时，桩1、桩2的漩涡脱落相位相同，与对称的桩4、桩3的漩涡脱落相位相反。

图 10 不同桩间距下并列4桩柱绕流瞬时速度云图(Re=4×106)(单位: m/s)Fig. 10 Flow instantaneous velocity cloud map of four pile-columns in parallel under different pile spacings (Re=4×106)(unit: m/s)

4.1.2 绕流水动力特性 如图11所示，并列4桩柱绕流各桩柱阻力系数随桩间距的变化表现出与串列4桩柱相同的趋势，均是先减小再增加又缓慢下降，直到L≥7D时，保持稳定在0.46；在L≥4D后，两桩柱阻力系数基本相等，桩柱间流场的干扰可以忽略不计。

各桩柱绕流升力系数随桩间距的变化曲线均表现出先减后增再增大，直到L≥7D时保持稳定在0.33。当L≥3D时，两桩柱的系数基本相等。由于桩2所处的位置，其流场两侧均受相邻流场干扰，故桩2的绕流升力系数大于桩1(见图12)。

图 11 桩柱绕流阻力系数随桩间距的变化(Re=4×106)Fig. 11 Change curves of drag coefficient around each pile with pile spacing (Re=4×106)

各桩柱绕流斯特劳哈尔数随桩间距的变化如图13所示，在桩间距L=2D时，由于桩柱绕流尾流流场间的强烈相互干扰，桩1、桩2的Sr存在明显差异；其后随L的增加，桩柱Sr的变化规律相同。在桩间距L≥3D时，两桩柱的Sr大小基本相等，可以忽略桩柱间流场的干扰；最终L≥7D时，Sr稳定在0.34。

图 12 桩柱绕流升力系数随桩间距的变化(Re=4×106)Fig. 12 Change curves of lift coefficient around each pile with pile spacing (Re=4×106)

图 13 各桩柱绕流系数随桩间距的变化曲线(Re=4×106)Fig. 13 Change curves of flow coefficient of each pile with pile spacing (Re=4×106)

《港口工程荷载规范》(JTS 144-1—2010)为了简便计算并列各桩柱的水流阻力，将并列各桩柱之间流场的相互影响用横向影响系数来量化。由于圆形截面桩柱的流线外形，横向影响相对较小，规范中并未给出圆形截面桩柱不同桩间距时的横向影响系数。将大流速下大直径并列4桩柱桩1在不同桩间距时的横向影响系数记为1，通过数值模拟，可得桩2在2D，3D，4D，5D，7D和9D桩间距下的横向影响系数分别为1.350，1.124，1.064，1.042，1.009，1.002。可见，随着L的增大，横向影响系数逐渐减小；在L=9D时，横向影响系数基本上为1，横向影响效应消失。在L≥4D时，基本可以不考虑并列桩柱间流场横向干扰对绕流阻力系数的影响。桩2的横向影响系数随桩间距增大而减小，最后趋于稳定。

4.2 流速变化影响

从图14可知两流场形式基本相同：各桩柱后方尾流中均形成稳定涡街，桩柱间流场干扰较小。由表4可知，流速在1～2 m/s时，基本可以忽略流速变化对并列桩柱绕流阻力系数和升力系数的影响。流速变化对并列各桩柱的Sr影响较大，流速越大，Sr越大，漩涡脱落频率越快。

图 14 不同流速下并列4桩柱绕流瞬时速度云图(L=4D)(单位: m/s)Fig. 14 Instantaneous velocity cloud map of flow around parallel four-columns at different flow rates (L=4D)(unit: m/s)

表 4 不同流速下并列4圆柱绕流主要系数统计(L=4D)Tab. 4 Main coefficient statistics of flow around parallel four- cylinders at different flow rates (L=4D)

5 结 语

基于CFD数值模拟方法，依托重庆港果园码头二期工程，进行了大流速下内河框架码头大直径单桩、串列4桩柱、并列4桩柱绕流水动力特性二维数值模拟，系统分析了不同流速及不同桩间距下桩柱绕流尾流流场形态、绕流系数Cd，Cl，Sr等水动力特性参数的变化，得出如下结论：

(1) 流速在1～2 m/s时，可以忽略桩柱升力与阻力系数影响；对Sr影响很大，随流速增大，Sr增大，漩涡脱落快。

(2) 对于串列4桩柱，随L的变化，桩柱尾流呈现不同的漩涡脱落形式，下游桩柱与上游桩柱之间干涉效应逐渐减弱。在桩间距[3D,4D]之间，存在1个临界间距，影响串列桩柱间涡街的形成；在L≥7D时，桩1、桩2后的流场形态与单圆柱绕流的流场形态基本相同。Cl随L的变化先减后增再减小；Cd在L=7D～13D时基本保持不变；Sr先减后增，桩间距L≥5D时基本保持不变。

(3) 对于并列四桩柱，各种桩间距下绕流流场对称。随L的变化，桩柱绕流尾流涡街呈现不同结构形式；相邻桩柱绕流流场间相互干扰程度减弱直至消失。桩间距L≥3D时，各桩柱系数Cl和Sr大小基本相等；L≥4D时，桩柱系数Cd基本相等，各桩柱绕流流场间的干扰基本可以忽略；L≥7D时，系数Cd，Cl和Sr均保持稳定，不随L变化。L=2D～5D时，相邻桩柱绕流流场的漩涡同步反相脱落；L=7D～9D时相邻桩柱绕流流场的漩涡同步同相涡脱落。