不同护坡方式下的河道堤防内波水动力特征试验分析
2020-03-10杨书山
杨书山
(辽宁省鞍山市岫岩县水利事务服务中心,辽宁 鞍山市 114300)
当前,河道堤防设计需要结合护坡方式确定其内波相应的水动力学特征,从而提高堤防在高洪期间受水力冲刷的稳定性[1]。而由于缺少相应的计算方程,对于内波动力学特征分析主要还依靠水槽试验进行[2- 6],这种方式下需要耗费大量的时间和经费,且不同护坡方式下其内波水动力特征不同,单一护坡方式下的试验方程很难具有通用性[7]。为此需要结合不同护坡方式进行试验分析,从而确定不同河道护坡方式下的内波水动力学特征[8]。近些年来,大型室内水槽试验成为研究河道堤防水力学特征的方式[9- 15],为此本文结合室内水槽试验方式,重点对碾压混凝土、浆砌石护坡、格宾石笼护坡、高性能加筋草皮4种常用护坡方式下,下河道堤防内波水动力特征进行分析,结合试验结果探讨相应内波下的水动力计算经验公式,研究结果对于河道堤防稳定性设计具有重要的参考价值。
1 试验方案
本次采用室内水槽试验方式,不同护坡方式下河道堤防内波的水动力特征进行分析。试验水槽长度为120m,宽度为3.5m,高度为2.5m。河槽泥砂厚度为30cm,边坡n为1∶2,底宽1.0m,每侧滩地宽度为0.37m,河槽剖面如图1所示。在河道堤防上游段每隔10m设置有流速仪以及自动水位计。在试验水槽内部设置深度为1.0m的测试区,用来设置不同护坡方式。设置的4种常用护坡方式如图2所示。在进行室内试验时,共进行24组放水试验,各种护坡方式均进行6组试验,部分试验结果见表1。
2 主要指标计算方程
主要计算河流水流内波的水动力特征,测定的主要指标为平均水深及流速均值的相关方程。主要通过建立水流内波的水深dm与流量qws之间的相关关系,相关方程为:
(1)
式中,dm—水流内波的平均水深,m;qws—断面流量,m3/s;Kdm—内坡水深相关经验参数,对于碾压混凝土、浆砌石、格宾石笼、高性能加筋草皮等四种护坡而言,其参数值分别为3.753、2.354、2.251以及2.143。
假定河流内波平均流速为断面水流流量与内坡平均水深的比值,则内波流速的均值计算方程为:
(2)
式中,νm—内波平均流速,m/s;其他变量同上述方程中的变量含义。
按谢才公式对方程进行转换,转换方程为:

图2 常用河堤护坡方式
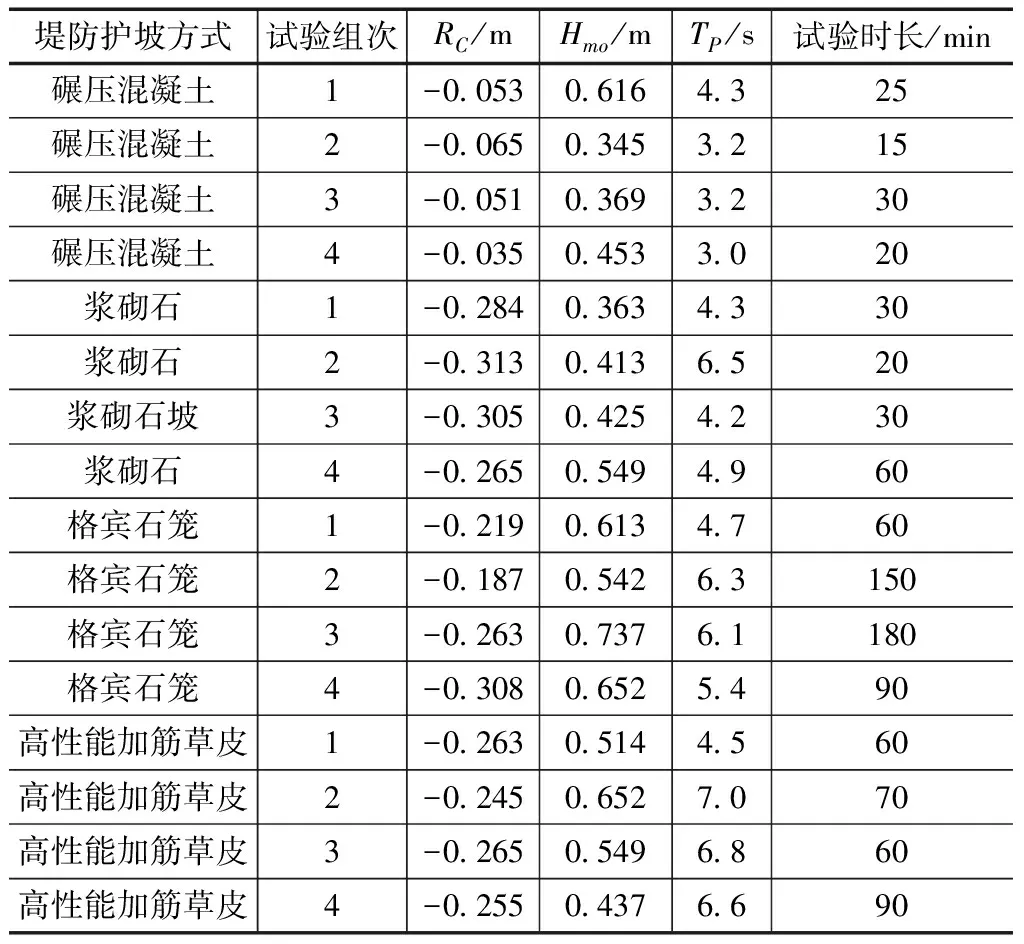
表1 各护坡方式下的部分试验组次数据
注:Rc为高出河道堤防的水面高度;Hmo为水流有效内波的高度;TP为水流内波谱周期
(3)
式中,θ—坡角,(°);fF—范宁摩擦系数;d—计算水深,m。
另方程中的两个系数相同,并采用内波角β替换方程(3)中的坡角θ,计算方程为:
(4)
在方程中结合试验内波比例可以推算出4种护坡方式下的范宁摩擦系数fF分别为0.0217、0.0652、0.1148、0.1045。因为方程中范宁摩擦系数并非严格意义上的摩擦系数,需要结合坡度和底摩阻进行内坡水深平均值的换算,计算方程为:
(5)
式中,fF*—转换的摩擦系数;其他变量同上述方程中的变量含义。
在内波平均水深计算的基础上,结合转换系数对其内坡平均流速进行转换计算,计算方程为:
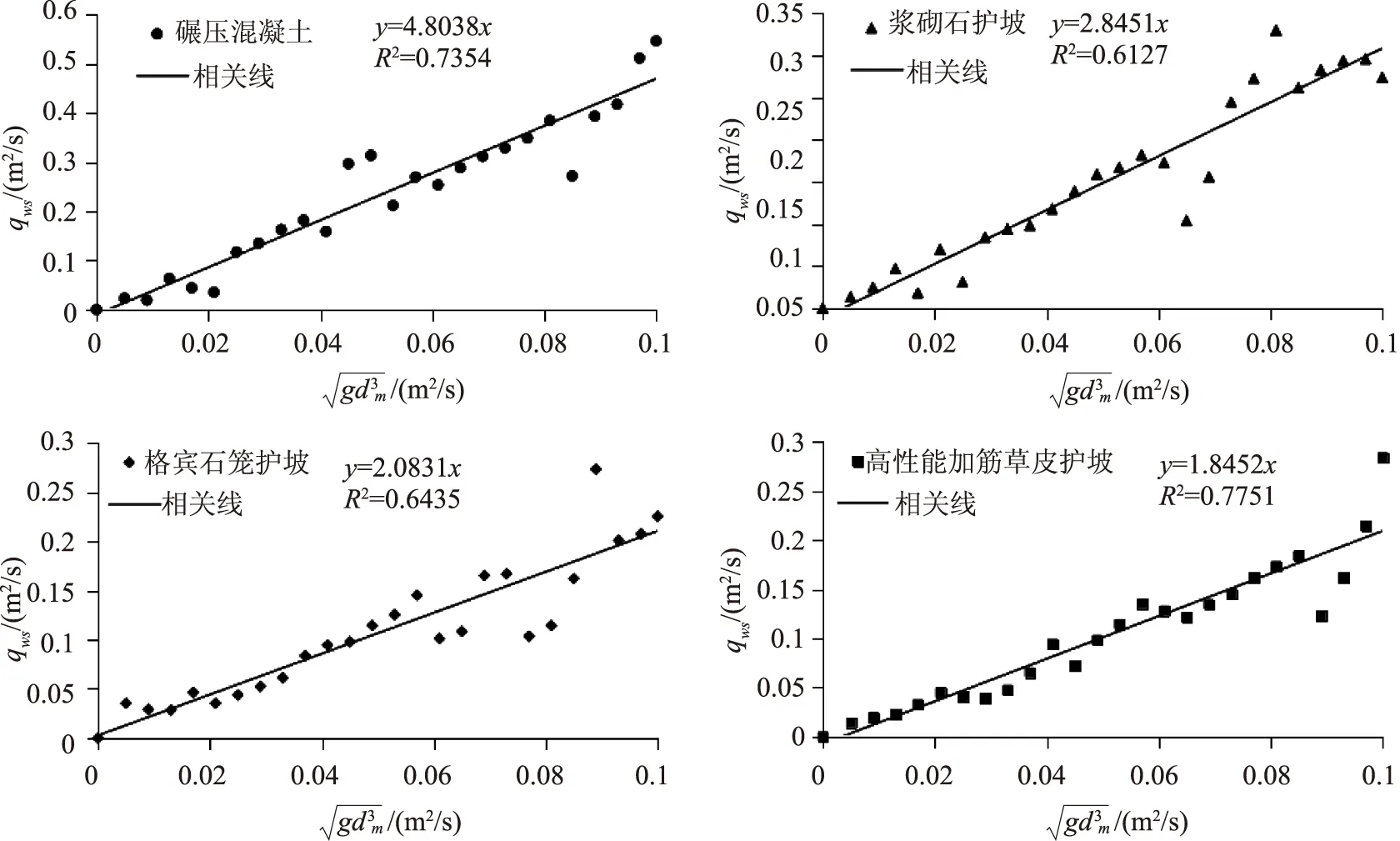
图3 不同护坡方式下波速和水深的试验结果
(6)
方程中内平均水深和流速计算的适用范围为0 结合水槽方式试验,分析不同护坡方式下内波平均水深与流速之间的相关关系,并分析不同护坡方式下波速和水深的试验关系,分析结果见表2及图3。 表2 不同护坡方式下内波平均水深与流速之间的相关关系试验结果 结合波速和水深的推求方程,对不同护坡方式下的内波波速与水深的相关关系进行了分析,从表2中可看出,波速与水深均呈现较为明显的线性关系,波速是水深的重要影响因素。高性能加筋草皮的相关系数最高,这种方式下的范宁摩擦系数最小,使得其内波波速与水深线性关系拟合度较高,浆砌石下相关系数最低,浆砌石增加了范宁摩擦系数,使得对应的波速减小,且与水深的相关关系减弱。通过不同护坡方式下的波速和水深的相关方程可看出,同一水深条件下,碾压混凝土下的波速最大,对堤防的安全影响程度较大。从图3中可看出,高性能加筋草皮水深较高的区域,波速散点约为集中,而其他护坡方式下水深较大的区域,其散点分布较为凌乱。 结合内波特征值波高计算值以及特征峰值水深下的拟合散点,探讨了特征波高与峰值水深的转换关系和曲线拟合方程,结果见表3及图4—5。 表3 不同护坡方式下河道堤防内波波高与水深的分布关系分析结果 从图4中可看出,各有效波高条件下的计算值和实测值的拟合度均较高,随着有效波高的递增,其拟合度有所减小,这一原因在于放水试验的时间较短,试验样本不能完全满足有效波高的计算。对于河道堤防而言,洪水波对河道堤防的冲刷影响主要在于特征峰值,从特征波高与特征峰值水深之间的曲线拟合关系可看出,当Rc逐步趋于最大时,特征峰值对于的水深逐步趋于稳定变化,这表明不同内波之间存在波谷为0的区域,当Rc达到最大值时,特征波高与特征峰值对于的水深相同,此外从图5中还可看出不同护坡方式下对各散点数据分布影响程度较小。结合表1中特征波高与峰值水深转换关系及其拟合曲线方程,可以对不同护坡方式下的特征波高与特征峰值水深进行换算。 图4 内波特征波高计算值与试验值对比结果 图5 内波特征波高与特征峰值水深之间的曲线拟合关系 结合测定的波速和水深试验数据,对不同护坡方式下的内波均方根波高与平均波速进行计算,结合计算数据,点绘其曲线拟合及相关方程,探讨不同护坡方式下的内波均方根波高与平均流速的简单计算公式,分析结果见表4和图6。 图6 不同护坡方式下的波高估算及波速试验拟合结果 表4 内波均方根波高与平均流速的简单计算方程 通过内波波高分布关系对特征峰值对应的水深及特征波高建立相关方程,因此基于内坡均方根即可计算内波不同特征下的波高和不同特征峰值下的平均水深。从图6中Hrms~Rc的关系中可看出,不同护坡方式下的各试验数据呈现较为明显的分布一致性变化,而vm~gqws呈现较为明显的线性相关,不同护坡方式对其线性相关影响程度较低。从图中还可看出,高性能加筋草皮不同相关关系的散点都分布在上端,这主要是因为高性能加筋草皮对河道堤防内波水动力特征影响程度较小,因此同一试验条件下的相关性更高,散点更为集中。结合表6不同护坡方式下的内波均方根波高与平均流速的简单计算方程,可以推算不同护坡下的特征波高及波速,方便工程设计计算。 (1)本文建立的特征峰值水深与波高的拟合方程可用来进行峰值水深的预测,适用范围为-0.31 (2)本文建立的均方根波高与平均流速计算方程适用范围为0 (3)四种常用护坡方式按影响程度高低划分为:高性能加筋草皮>格宾石笼>碾压混凝土>浆砌石。 (4)本文重点分布不同护坡方式下对局部试验断面内波水动力特征的影响,但为探讨其沿程水动力特征的变化,存在不足。3 试验结果
3.1 内波平均水深及平均流速相关关系

3.2 内波波高与峰值水深分布关系
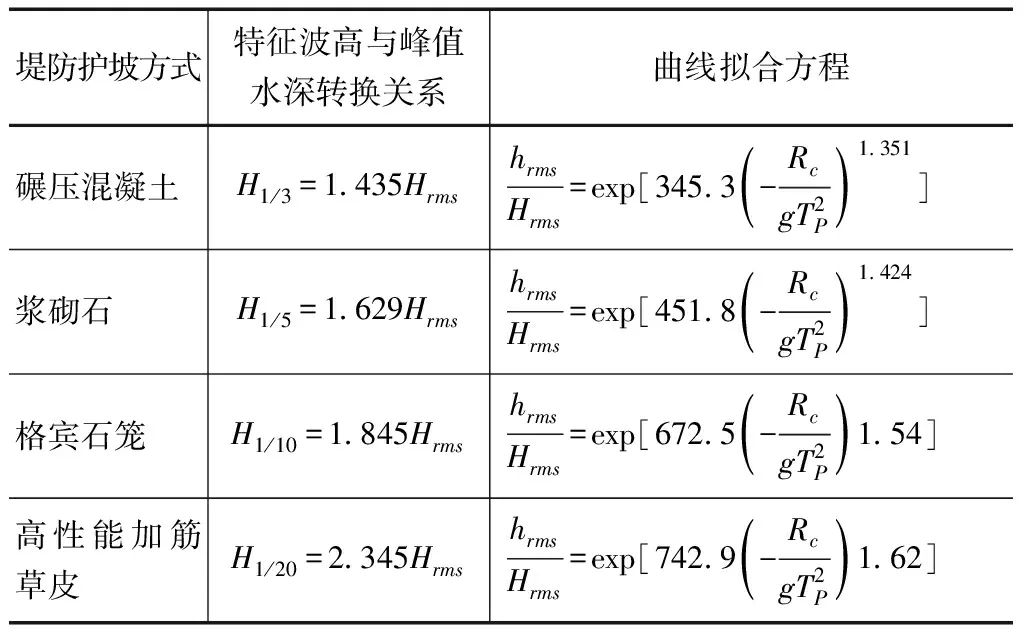

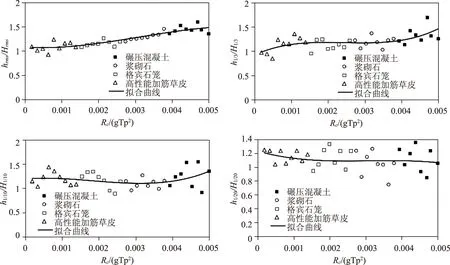
3.3 内波均方根波高与平均波速的计算
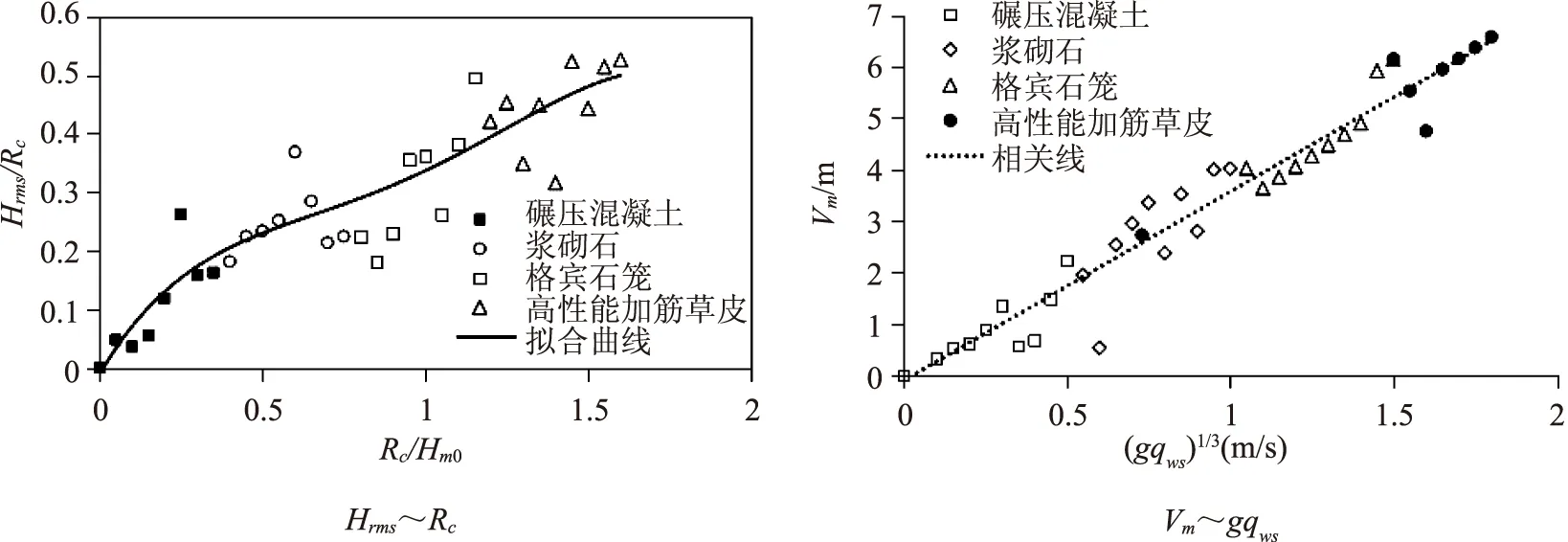

4 结语
