经编机梳栉电子横移伺服的最优滑模控制

汪健东， 夏风林,2， 李亚林， 赵钰宁

(1. 江南大学 教育部针织技术工程研究中心， 江苏 无锡 214122；2. 生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122)

经编伺服系统允许梳栉进行横移运动的时间极为短暂，因此要求经编横移伺服系统具有极高的动态响应和精确的高速定位[1]。目前对经编伺服控制系统的研究主要集中在比例积分微分(PID)控制，以及线性最优控制的研究上，其中，张琦等[2]分别建立伺服电动各部分控制模型，并整合成电子横移系统整体结构的动力学模型。郑静等[3]分析了脉冲宽度调制功放和电流反馈与调节环节增大速度比例增益有利于提高电子横移系统的动态响应性；闻霞等[4]基于伺服开环系统，设计了基于最优线性控制理论的控制器设计，提高系统的稳态精度和动态性能，实现了无静差高精度控制。在针对目标参数不变且无外界因素干扰的情况下，上述系统均具有很好的动静态性能[5]。但是，实际操作过程中，由于存在梳栉上不易安装末端执行机构监测装置，以及梳栉横移时产生的振动影响光栅尺等信号反馈装置的检测精度等问题，均会对横移系统性能产生影响[3]。所以，为解决横移过程中存在的不稳定因素，通过在原有控制理论的基础上引入滑模控制，以达到提升横移系统的鲁棒性。本文以线性最优控制设计为基础，结合滑模控制方法，通过进行合理滑模面设计，消除外部不确定因素对系统的干扰，并由MatLab仿真验证方法的有效性。

1 经编横移伺服系统工作原理

经编横移伺服系统主要分为直线伺服系统和交流伺服系统，目前交流伺服系统因其价格相对低廉，大多数经编机横移伺服系统均采用交流伺服横移系统。以交流伺服系统为例，该系统主要由上位机、控制卡、驱动装置和信号检测等部分组成[6]，其原理如图1所示。

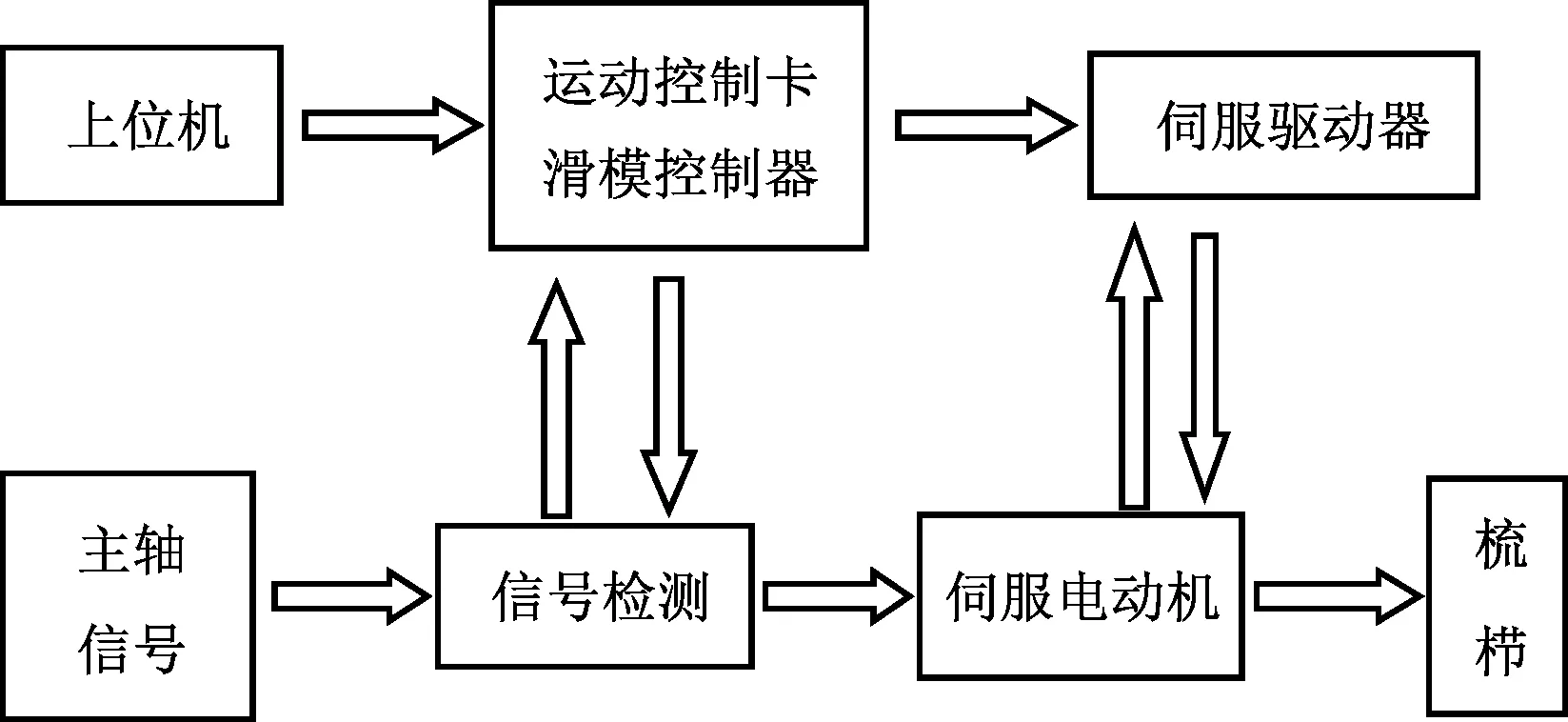
图1 电子横移系统工作原理Fig.1 Working principle of electronic transverse shift system

经由上位机输入织物的花型信息，对数据处理后通过CAN(controller area network)总线与运动控制卡进行数据交换，将横移信息存储到控制卡。当织针进行横移运动时，运动控制卡通过接收到的主轴光电编码器的信号，向伺服驱动器按一定的频率发送指令脉冲信号，由此决定横移量和横移速度。驱动器驱动伺服电动机实现横移运动，横移的当前位置由光电编码器不断进行测量，运动控制卡将检测到的信号和命令信号进行对较获得偏差数值[7]，并进行偏差补偿，负载存在扰动时，伺服电动机转速会产生较大的动态偏差，滑模控制器可以有效地控制干扰信号影响，实现梳栉的精准横移。

2 经编横移交流伺服模型的建立

经编电子横移伺服系统数学模型由电气传动机构和机械传动机构组成[3]，其传动原理是以控制电压作为输入，电机轴的角位移与角速度作为输出，电机轴通过与之连接的联机轴直接驱动滚珠丝杠进而推动梳栉进行横移运动。

2.1 电气传动机构模型

为有效地进行横移运动，伺服电动机在转动过程中以电压为输入，转子速度为输出，通过对电动机电磁转矩进行控制，从而获得满足指令信号要求的电动机角位置、速度和加速度。交流伺服电动机的物理模型如图2所示。

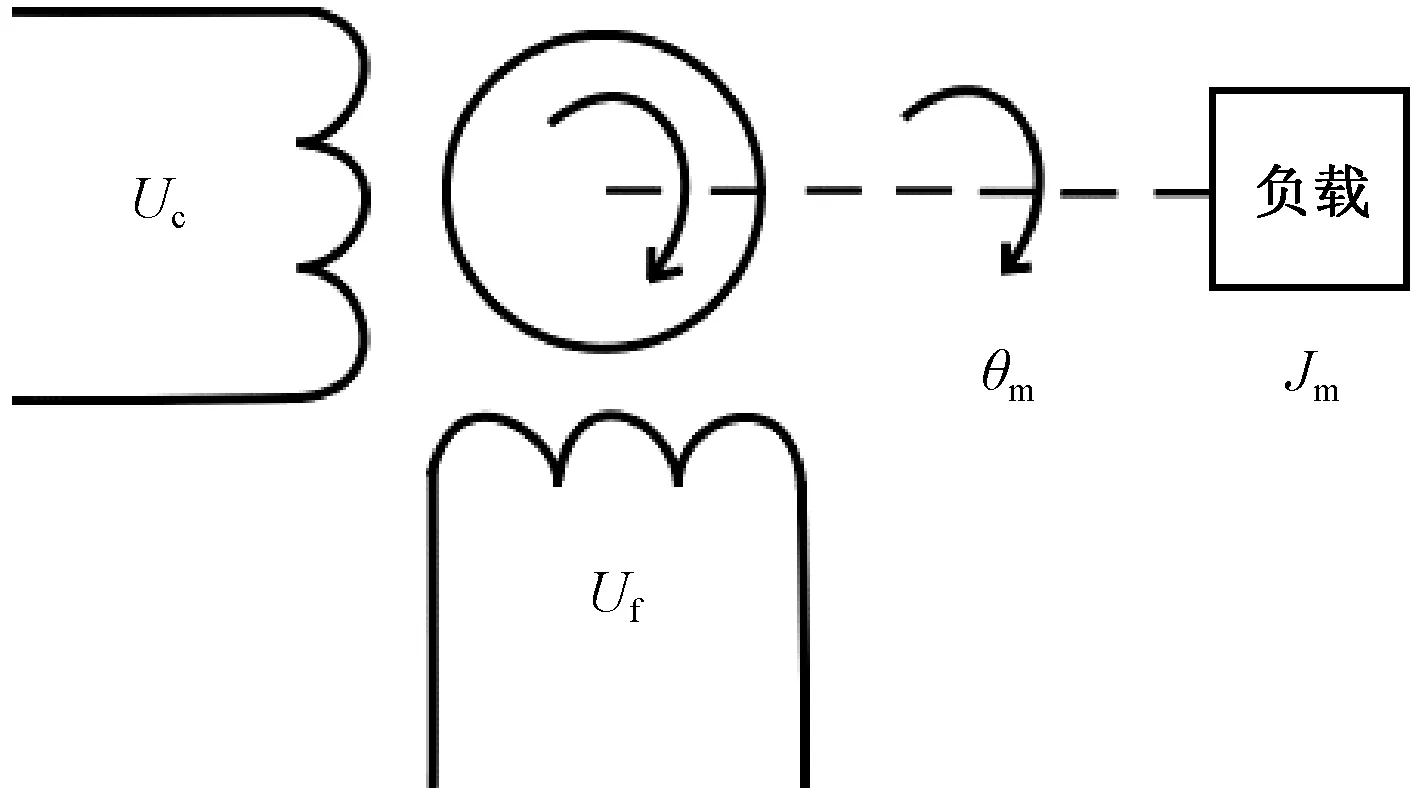
图2 交流伺服电动机物理模型Fig.2 Physical model of AC servo motor

电动机在匀速运动过程中其动态方程为

(1)

式中：Jm为伺服电动机转子转动惯量；fm为伺服电动机等效黏性摩擦因数；θm为伺服电动机角位移；Ku、kw为正常数；Uc为控制电压。

2.2 机械传动机构模型

机械传动机构主要由驱动电动机、同步传动机构、滚珠丝杠、丝杠支承轴承和滑轨机构组成[6]。机械传动以电动机的角位移作为输入，梳栉的直线位移为输出，机械传动机构如图3所示。电动机通过同步传动机构与滚珠丝杠相连，通过滚珠丝杠驱动梳栉作直线运动[2]。

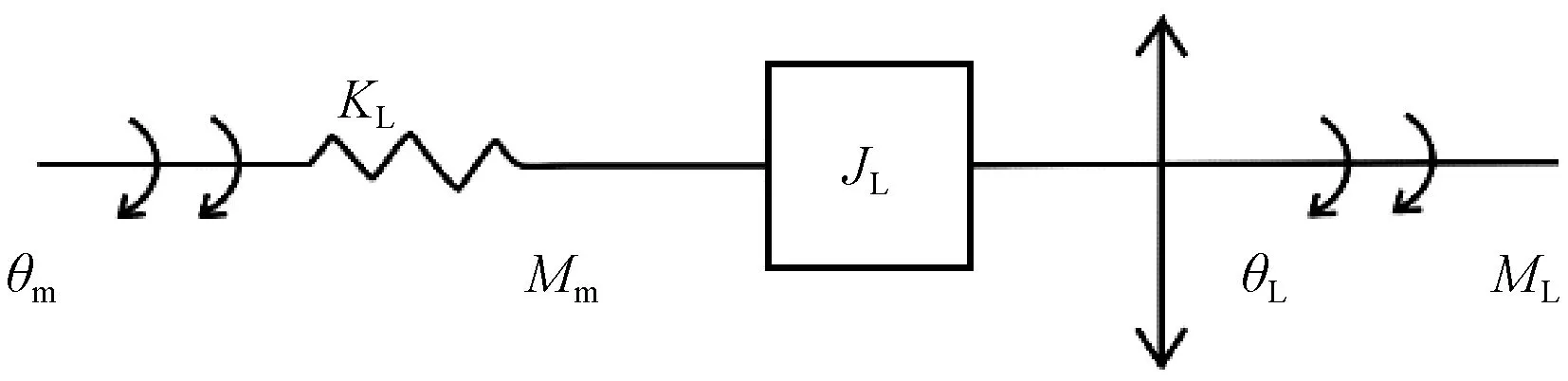
图3 机械传动模型Fig.3 Mechanical transmission model

根据刚体转动规律，滚珠丝杠的动态平衡方程为

(2)

式中：ML为丝杠输出转矩；Mm为电动机电磁转矩；Jn为机械部分在丝杠上的转动惯量；ipt为丝杠螺母副的传动比。

将式(1)、(2)结合，得到整个伺服系统的动态平衡方程为

(3)

式中，ω为未建模的动静态干扰。

由式(3)得出以电压Uc为输入和以丝杠角位移θ为输出量的运动方程：

(4)

将式(4)改写为式(5)所示的伺服系统状态空间表达式：

(5)

式中：x为系统状态变量；y为系统的输出变量；u为系统的输入变量;d(t)为系统参数不确定部分在内的未建模动态等有界扰动。

3 最优滑模控制器设计

伺服要完成2次加减速的过程，这也就要求伺服系统需要加速及响应性能。电动机在带动滚珠丝杠进行运动时进行高频率的“运动—静止—运动—静止”过程中，要求各机械部件之间应具有很高的抱合度[1]。但是由于安装和加工精度的问题，在安装过程中各部件之间难免会存有缝隙，在经编机进行高速运动时会导致机械部件之间的运动不同步，最后导致梳栉的运动规律不符合运行前设定的梳栉运动规律曲线[8]。

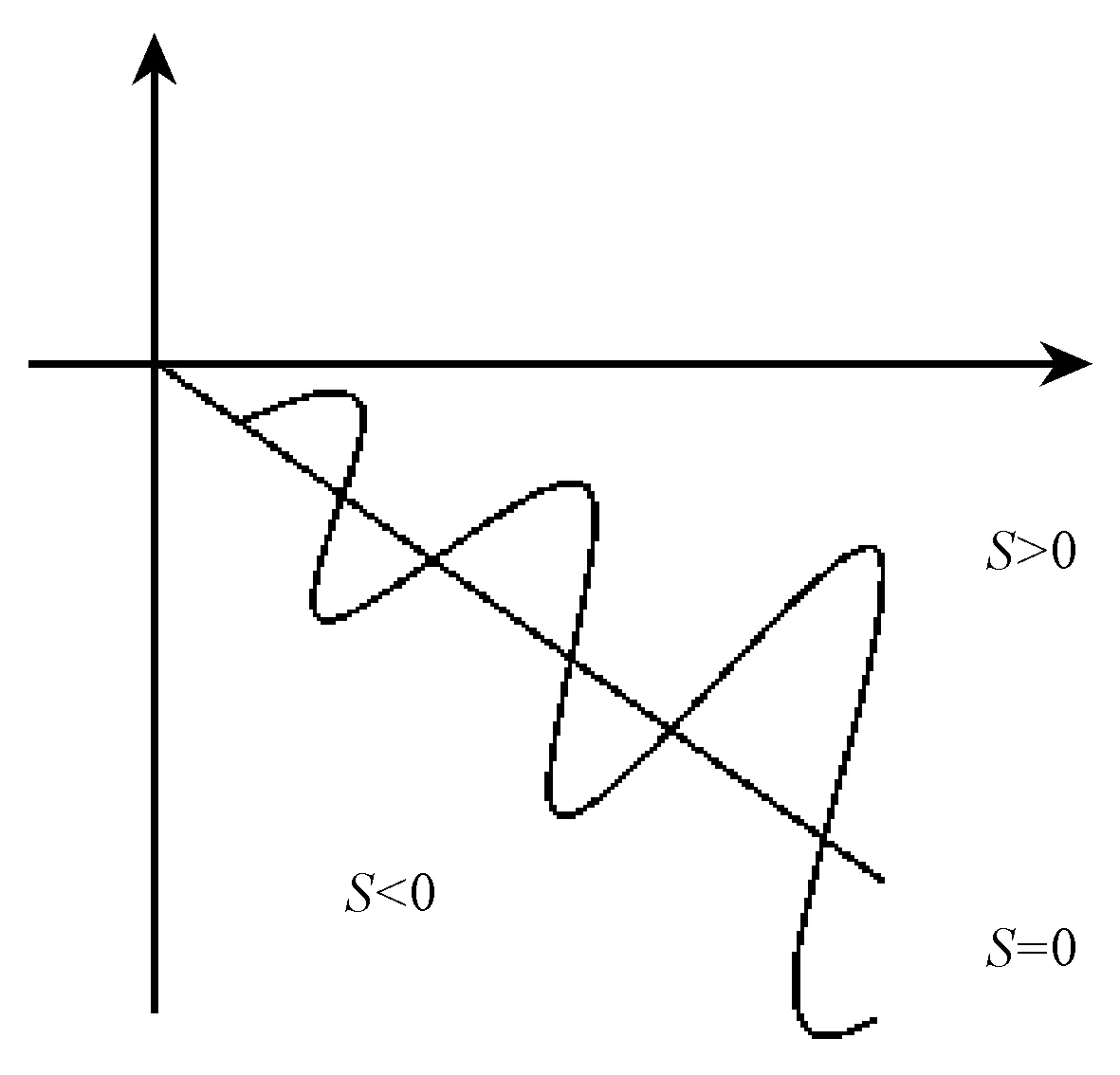
图4 滑模切换面Fig.4 Sliding mode switching surface

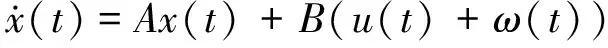
(6)

3.1 最优线性控制系统

基于式(6)可得出线性方程(7)。根据最优线性控制理论，设计u(t)使得性能指标J最小：

(7)

(8)

式中：tf为控制的终止时间；s为系统终止约束条件；Q和R为加权矩阵。

构造Hamilton函数，使得J值最小：

(9)

(10)

即最优控制信号为

u*=-R-1BTPx(t)=Kx(t)

(11)

式中：P为正定常数对称阵，为Riccati方程的解；K为最优状态反馈增益矩阵。

得出此时闭环系统的动态方程为

(12)

3.2 滑模控制积分滑模面的构造

基于式(6)采用积分滑模理论进行滑模面的构造，所构造的滑模方程如式(13)所示：

(13)

式中，C为正常数矩阵。

(14)

则其等效控制率为

(15)

将式(15)带入式(6)，得出最优滑模控制方程：

(16)

根据最优控制理论，式(12)的解为线性闭环系统下的最优轨线。最优滑动模控制式(16)与最优线性闭环式(12)形式相同, 即上述构造的最优积分滑模面式(13)可产生与线性闭环系统式(12)一样的最优运动轨线。

3.3 最优滑模控制律设计

最优滑模控制律设计见下式：

(17)

则：

(18)

依据滑模控制的实现要求，式(18)函数满足设计的要求，所以设计出的最优滑模控制律满足实现条件，即系统的轨线在最优滑模控制律的作用下能在有限的时间运动到滑模切面并保持在上面。

4 系统仿真

为验证最优滑模控制的有效性，在MatLab软件进行系统的仿真。伺服电动机型号为TBL-iⅡ，其电动机参数如表1所示，表2示出机械传动机构参数。

表1 TBL-iⅡ型伺服电动机主要性能参数Tab.1 Main performance parameters of TBL-iⅡ type servo motor

表2 机械传动机构参数Tab.2 Mechanical transmission mechanism parameters

根据表1、2的参数可得，A=[0 1;0 -8]，B=[0;15]。在MatLab中通过调用lqr()函数可求得K=[1.000 0.657 4]。横移过程中梳栉以一定的速度完成整个横移运动，以避免在横移始末产生过大的加速度，造成冲击。因此，梳栉的运动曲线应选择速度、加速度和跃度都相对平滑的曲线，从而使得梳栉的运动柔和，冲击力减小[8]。在MatLab中采用正弦曲线r=0.5sin(2πt)为输出，正弦曲线E=0.1sin(2πt)为干扰信号。分别对最优线性模型以及最优滑模控制模型进行仿真。其结果如图5所示。

通过图5(a)可知，在无干扰的情况下，最优线性系统与最优滑模控制系统二者的位置响应曲线基本重合，验证了所设计的最优滑模控制系统具有与最优线性控制系统一样良好的动静态性能。通过图5(b)和(c)可以看出，在外加干扰的情况下最优线性控制系统位置曲线上方出现明显的波动且持续进行，将影响原有系统的稳定性；而最优滑模控制系统在干扰出现波动后，极短的时间内趋向于稳定状态，使得整个响应曲线按照原有的位置响应曲线继续进行下去。

图5 2种系统仿真结果Fig.5 Simulation results of two systems. (a) Position response curve of two systems without interference; (b) Position response curve of optimal linear control system when interference is added; (c) Position response curve of optimal sliding mode control system when interference is added

图6 系统的单位阶跃响应曲线Fig.6 Unit step response curve of system

将系统仿真时间设置为1 s，在t为0处，突加一幅值为1的信号到系统上，其系统单位阶跃响应曲线如图6所示。可以看出最优滑模控制系统与参考系统相比，具有快速响应性能。系统在3.5 ms左右振幅达到最大，之后振荡渐渐收敛，在12 ms左右振幅趋近1，说明此时系统完成调整，达到稳定。因此，通过仿真振荡到逐渐收敛进而快速趋向于稳定，验证了所设计系统的准确性与稳定性。

综上所述，最优滑模控制具有最优线性控制的快速响应性能，良好的跟随性，以及滑模控制的抗干扰性能。在经编横移伺服系统中引入最优滑模控制方法，能有效地提高系统的稳定性，对梳栉横移时产生的振动影响反馈装置的检测精度等干扰因素，具有很好的抑制作用。

5 结束语

通过分析经编机横移运动原理，建立经编机横移伺服数学模型，设计出基于最优线性控制和滑模控制原理为基础的最优滑模控制系统。经MatLab仿真验证结果表明，最优滑模控制既具有最优线性控制的快速响应性能，良好的跟随性，同时也具有滑模控制的抗干扰性能。经编横移伺服系统中使用最优滑模控制方法，能有效地对经编机横移过程中产生的干扰因素进行控制，提升伺服系统的稳定性。

FZXB