纱条中纤维排列状态与纱条不匀的关系
2020-03-10苏玉恒孔繁荣严广松
苏玉恒, 孔繁荣, 严广松,2
(1. 河南工程学院, 河南 郑州 450007; 2. 郑州升达经贸管理学院, 河南 郑州 451191)
在短纤维纺纱中,无论是本身长度不同的棉纤维还是长度趋同的化学纤维,由于加工过程的各种作用,最终在纱条内部都表现为长度不同,这种不同长度的纤维在纱条中复杂的排列状态是造成纱线不匀的基本原因,因而研究纤维在纱条中的空间几何形态及其在纱条中的排列是纱条不匀理论的重要基础研究之一。
纱条中短纤维的排列特征早期用纱条截面中纤维的根数来表示,1941年,Spencer-Smith等[1]提出等长纤维的纱条截面内的纤维根数服从泊松分布,从而用时间序列方法给出了计算纱条不匀的方法;1945年,Martindale[2]在泊松分布理论基础上,给出了纱条的极限不匀以及不匀指数,奠定了纱条不匀研究的理论基础。但实际上,纱条中的短纤维不是等长度的,纱条截面的纤维根数作为表示纤维排列状态的指标已经不能满足要求,很多研究者将纤维头端的分布引入,来定义纤维在纱条中的随机排列状态,其中Rao[3]关于理想纱条的定义被广泛认可,Brown等[4]建立了纱条片段长度、纤维长度分布与片段中纤维头端数目的统计模型;Zeidman等[5]将纱条不匀分解为截面内纤维根数的分布不匀、纤维细度不匀和纤维倾斜度的差异,并给出了纱条截面内的纤维根数与纤维长度分布、纤维头端密度间的函数关系,但忽视了它们的随机特征;Cherkassky[6]则认为纱条中相邻纤维间的间距服从指数分布;YAN等[7]在假定理想纱条中纤维全部排列在多个通道中,构建了一种纤维排列的假构模型,并以通道中相邻纤维的头端间距为参数,给出了一种纱条极限不匀的新表征方法;张弘强等[8]利用示踪纤维法测试了梳棉条中纤维左头端的分布,经检验认为梳棉条中纤维左头端沿条子轴向呈均匀分布;JIANG[9]采用纱条内纤维左头端呈均匀分布的假设,模拟了随机纱条,用于纱条强力性能的分析。以上研究成果可以看出,以纤维头端分布形态作为纤维在纱条中的排列特征的描述指标是一种较常见的做法,但其分布形态与纱条截面纤维根数及纱条不匀间是什么关系,梳棉条中纤维左头端沿条子轴向呈均匀分布的实验结果是否适用于平行度更高的纱条等问题仍需进一步解析。
本文以纱条内纤维头端数的分布为纤维排列的标志特征,构建纱条中纤维排列几何模型,使用Monte Carlo方法,进行随机纱条的排列模拟,获得各种不同分布形态及参数下的纱条截面纤维根数CV值,并对其影响因素和规律进行了分析。
1 纱条内纤维头端分布的几何模型
1.1 假设条件与几何模型
本文所研究纱条为纤维沿轴线平行随机排列的连续线性集合体;所谓随机排列是指在集合体上任取一区间,某一根纤维的特定位置(如左头端)出现在该区间内的可能性与区间的大小成正比,进而假设:1)集合体中所有纤维具有相同线密度,且沿纤维长度方向均匀一致;2)集合体中每个纤维头端(右或左)的位置相互独立,并且与其长度无关。
在上述定义的随机纱条上任意选一点x及其相邻截面x+Δ,形成宽度为Δ的区间[x,x+Δ),对于每一根纤维而言,以纤维左头端为纤维位置标志,其位置只有2种可能性,落入上述区间或在区间之外,且对每一根纤维都是相互独立的,因此落入区间[x,x+Δ)的纤维左头端数是典型的n重Bernoulli模型。在Δ较小(如1 mm)的情况下,假设进入[x,x+Δ)区间内的纤维左头位置在区间内均匀分布,那么在明确区间内头端数量分布形态的情况下,就可以构建如图1所示的连续纤维集合体模型,并计算其统计特征。
1.2 模型的统计特征分析
根据前述假设和几何模型,在纱条上任选一个截面的位置,如图2所示的连续纤维集合体的纤维左头端几何统计模型中xN处,在给定区间宽度Δ的情况下,向右分割出若干个区间,直至处于xN截面内的所有纤维的左头端均处于最左区间分界点的右侧,即处于截面xN内的所有纤维中,其左头端所在的最远位置在图2所示的[x1,x2)区间内。设ξ为xN处的纤维根数,则ξ的数量是由那些左头端位于截面xN左侧各区间内并向右延伸至xN截面的纤维的数量所决定,各区间的分界点为xN,xN-1,…,x1,因而有:
ξ=η1+η2+…+ηi+…+ηN-1
(1)
(2)
式中:N为纱条上分割区间的分界点数,N-1为分割出的区间数;Δ为分割区间的宽度,mm;lmax为纤维长度取值的上限,即纤维集合体中最长纤维的长度,mm;ηi为左头端在第i区间内的纤维向右延伸到xN截面的纤维根数;i为区间的序数,i=1,2,…,N-1。
ηi=ζi1+ζi2+…+ζis
(3)
式中:s为第i区间内的纤维左头端个数,是n重Bernoulli模型的随机变量,s的分布形态可有二项分布、泊松分布及固定值等。
假设服从s~b(n,p)的二项分布,n表示实验次数,p表示事件发生的概率,且与ζij独立。显然有:
(4)
式中:j为头端个数,j=1,2,…,s。
那么纤维左头端在某个区间内的纤维延伸进入截面xN的概率为:
P{左头端在[xi,xi+1)区间内的纤维延伸到xN}=
P{L>((N-i-1)Δ+δ)}
(5)
式中:L为纤维长度,即服从密度函数f(x)的随机变量,mm;δ为纤维左头端在区间[xi,xi+1)内的长度。
按前述定义δ为一个[0,Δ]区间上的均匀分布,其密度函数为:
(6)
由δ与L相互独立,则其联合密度函数为:
(7)
0 则有: (8) 由此可得: (9) 根据随机多个随机变量的期望的计算方法,对式(2)求数学期望,有: E(ηi)=E(s)E(ζij) (10) 所以,有: (11) 根据前述假设,则有: (12) 式(12)是通过截面xN的纤维的平均数,即随机纱条截面的纤维平均根数。由其可知通过纱条截面xN的纤维平均根数的与n、p以及f(x)有关,其中n和p决定了其分布,当纤维长度分布函数和纱条截面纤维根数的期望已知的条件下,即可得到np,由于p∈[0,1],显然,p可单独成为描述随机纱条中纤维排列的参数。 1)确定纤维长度分布的密度函数。目前棉纤维长度分布的密度函数估计是由林倩等[10]提出的非参数核估计方法和混合方法,本文采用非参数核估计的方法,其给定的正态核函数的棉纤维长度分布密度函数估计的表达式如下。 (13) 2)Nty为设计纱条的线密度,tex;Ntf为纤维的平均线密度,tex,显然模拟纱条截面纤维根数的期望如式(14)所示。 (14) 3)确定区间宽度。根据前述假设当区间宽度增大时,所分割区间数量减少,区间之间的随机性下降,区间内纤维左头端数量增加,其分布将趋向均匀分布,反之将趋向泊松分布,因此区间宽度应合理选择,本文暂选区间宽度为1 mm。 4)确定lmax的值。lmax是纤维长度取值的上限,其目的是保证进入xN截面的所有纤维的左头端均在x1截面的右侧,其取值大于或等于最长纤维长度,通常棉纤维最长不会超过45 mm,因此lmax的值可取45 mm,理论上也可以取更大的值,超出最长纤维后的积分将为零,实际并无意义;另一方面lmax的取值也要保证与区间宽度的比值为整数,即保证区间为等分区间。若区间宽度为1 mm,取lmax=45 mm,则N=46,区间数为45。 5)将式(1)、(2)、(3)、(4)所选参数代入式(12),即可计算np值。 7)依据给定的纤维长度分布的密度函数式(13),随机生成n个随机纤维的长度值,并分配给εi。然后对每个εi,随机生成对应数量的[0,1)区间的均匀分布随机数,作为该区间内这几个纤维左头端所在的位置,这样就相当于将纤维逐个区间,随机排列起来构成了一个连续纤维纱条。 8)对步骤7)生成的纱条进行观测,并统计x45截面上的纤维根数。 9)反复7)、8),可得到x45截面纤维量统计数据,并可计算其统计特征。 10)在选择不同p值的情况下,重复6)至9),可得到不同p值下纱条截面纤维量的统计特征值,如CV值等。 1)模拟条件。从某纺织厂实际抽取2种不同配棉的熟条试样,分别称为“试样1”和“试样2”,在Premier大容量棉花检测仪(印度Premier电子有限公司)上测试获得纤维长度的根数分组数,其中试样1的根数分布见图3。将试样1的数据代入式(8)可以得到试样1的纤维长度分布密度函数。同时,实测该棉纤维熟条试样中纤维的平均线密度为1.56 dtex,所纺出实际纱条的线密度为14.5 tex。由此可计算出纱条截面纤维根数的期望为93.4个,代入式(7)计算出区间内纤维头端数的期望为4.2个。 2)模拟结果分析。不同p值时的纱条截面根数CV值(s~b(n,p))(试样1)见图4。p值与CV值间基本呈负线性关系,随着p值增加,根数CV值减小;对于二项分布,当p趋向1时,其分布趋向每个区间内具有相等左头端数的因定值,而当p趋向0时,则趋向于泊松分布。这个结果表明当区间内左头端数为固定值时,纱条截面纤维根数不匀为最小,此时纱条内各根纤维的左头端位置应是均匀分布状态;当区间内纤维左头端分布为泊松分布时,不匀最大,此时纱条内各根纤维的左头端分布为完全随机状态。如果以固定值和泊松分布对上述相同的纱条截面根数CV值进行模拟,固定值时的CV值为4.99%;泊松分布的CV值为10.38%。结果也表明在给定纤维长度分布的情况下,p值反应纱条内纤维排列的状态,并直接影响到不匀的大小。 还有2个因素会影响到CV值的大小,一是纤维的长度分布形态,二是间距划分的大小。试样2的纤维长度根数分布见图5,运用前述方法计算不同p值时的纱条截面根数CV值(s~b(n,p))见图6。其固定值时的CV值为3.74%,泊松分布的CV值为10.09%。从图形和数据来看,长度分布的变化对CV值的影响并不大。 不同间距下截面纤维根数的CV值模拟结果(试样1)见图7。 图7示出,除区间宽度为45 mm外,其他情况下的CV值变化曲线并无太大变化,由于在区间宽度为45 mm时,所划分的间距数量只有1个,不存在间距之间纤维左头端数量的差异变化,纤维在区间内均匀排列,因此CV值相对较为稳定,但数值较大,主要受每次拟合时的排列纤维总根数的变化影响。其余不同区间宽度取值下的CV值变化基本没有差异。 本文提出了一种连续纤维纱条的排列方法,以左头端的分布表征纤维在纱条中的排列,给出了纱条截面内纤维根数与划定区间内的左头端数期望间的数学模型。利用这个模型对已知纤维长度分布的棉纤维试样所构成纱条的截面纤维根数CV值进行了模拟,经对模拟结果分析,得出如下结论。 1)纱条截面纤维根数的期望与划定区间内纤维左头端个数的期望成正比关系,其比例系数由间距划分和纤维长度分布决定。 2)在假定区间内纤维左头端分布为二项分布的条件下,纱条截面纤维根数CV值的变化与二项分布的参数p呈负线性关系,随着p值趋向于1,CV值显著减小。 3)通过改变区间宽度和纤维长度分布形态,对截面纤维根数CV值进行模拟,结果表示区间宽度和纤维长度分布变化,对该CV值影响较小,可见在这种排列方法下,CV值的变化仅与p值大小有关,因此p值可做为表示纱条内纤维排列状态的表征参数。 4)纤维长度分布与纱条截面纤维数的不匀无关。 5)本文所提出的连续纱条的排列方法,可用于纱条极限最低不匀的预测、纤维集合体性能研究以及纤维集合体加工过程的理论分析。 6)本文所模拟的纱条截面纤维根数不匀与实际纱条的不匀存在较大差异。因为实际纱条的不匀测试是纱条上一定长度(细纱为8 mm)片断间的CV值,因此二者之间的关联性还需进一步研究。
2 随机纱条的模拟与分析
2.1 随机纱条模拟的步骤

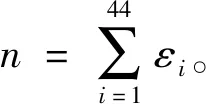
2.2 模拟结果
3 结 论
